Beschreibung im Zeitbereich
Du willst wissen was Systeme, Regelungen und Signale eigentlich sind? Keine Sorge, in diesem Beitrag erklären wir es dir!
Inhaltsübersicht
Differentialgleichung nutzen
Als erstes wollen wir ein System anhand einer Differentialgleichung beschreiben! In den Videos zu Übertragungsgliedern hast du erste wichtige Begriffe kennengelernt. Du hast bereits im Hinterkopf, dass Systeme Ein- und Ausgangsgrößen besitzen und dass ihr Verhalten durch Funktionen, wie beispielsweise die Übergangsfunktion, abgebildet wird. Eine erste Beschreibung eines Systems hast du ebenfalls kennengelernt: das Blockschaltbild!
Um mit Differentialgleichungen zu arbeiten, legen wir erst einmal gemeinsam ein Fundament und klären den Begriff „Signal“. Ein Signal ist im Allgemeinen ein Zeichen mit einer Bedeutung. Es kann dazu dienen Informationen zu transportieren. Ein kontinuierliches Signal besitzt einen Verlauf, in dem es zu jedem beliebigen Zeitpunkt definiert ist. Man kann also jedem Zeitpunkt ein konkretes Signal beziehungsweise einen Wert zuordnen. Ein Beispiel dafür ist der Spannungsverlauf an einem Mikrofon. Wir sprechen hier von einem zeit- und wertekontinuierlichen Signal! Für unsere Betrachtungen werden wir uns nur mit dieser Art von Signalen beschäftigen.
Dynamische Systeme
So, kommen wir als nächstes zu Systemen: Besitzt ein System Energiespeicher, wie zum Beispiel einen Kondensator, nennt man es „dynamisch“. Diese Systeme beschreiben meist Prozesse in unserem täglichen Leben und lassen sich anhand einer oder mehrerer Differentialgleichungen beschreiben.
So auch ein einfaches elektrisches System, ein RC- Netzwerk:
In unserem Video zu Bauteilen der Elektrotechnik kannst Du Dir die grundlegenden Funktionen der hier beteiligten Elemente nochmals in Erinnerung rufen.
In unserer Schaltung befindet sich eine Spannungsquelle und ein Strom, die wir als ideale Quellen betrachten. Ideal bedeutet, dass sie stets definierte Ausgangssignale liefern. Zudem haben wir einen Widerstand und einen Kondensator.
Jetzt benötigen wir die Maschinengleichungen dieser Bauteile, um die Ausgangssituation zu schaffen. Für den Widerstand R gilt:
Und für den Kondensator C:
Ziel ist es, die Spannung 
(t) am Kondensator zu berechnen, wenn wir unsere Spannungsquelle 
(t) einschalten. Unsere Spannungsquelle ist dabei konstant und verändert die Spannung nicht. Als Anfangszustand unseres Netzwerks wählen wir den Zeitpunkt t gleich Null und setzen fest, dass die Spannung hier (t) = 0 zu betragen hat. Beim Einschalten lädt ein Strom i(t) den Kondensator mit der Kapazität C auf und fließt so lange, bis die Spannungsdifferenz an unserem Widerstand zu Null wird. Sind alle Spannungsdifferenzen in einem Netzwerk ausgeglichen, bezeichnet man diesen Zustand als Gleichgewicht. Jetzt können wir in die mathematische Beschreibung übergehen.
Kirchhoffsche Gesetze
Zur Bilanzierung unseres Systems benötigen wir das erste Kirchhoff‘sche Gesetz, die Knotengleichung und als Nebenbedingung das zweite Kirchhoff’sche Gesetz, die Maschengleichung:
Aufgrund der Knotengleichung entspricht der Strom am Widerstand jetzt dem Strom am Kondensator und somit dem Gesamtstrom.
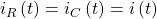
Mithilfe der Maschengleichung schreiben wir unsere Spannungen auf: 
Die Spannung am Widerstand 
wird deshalb negativ gewertet, da die Spannungsrichtung bei Ohm´schen Widerständen der Stromrichtung entspricht. Wenn wir uns die Gleichung für die Spannung U zur Hilfe nehmen, können wir die Spannung am Widerstand durch den Strom und den Widerstand ersetzen: 
Der Strom 
am Widerstand entspricht im Gleichgewichtszustand dem Strom 
am Kondensator und kann mithilfe der Beziehung zwischen Strom, Kapazität und der Spannung
noch weiter umgeschrieben werden:
\bigm
Setzt Du das jetzt in unsere Maschengleichung ein, erhältst Du nach der Eingangsspannung (t) umgestellt:
+ 
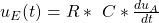Das ist die Differentialgleichung, mit der wir unser Netzwerk beschreiben können. Es handelt sich hierbei um eine Differentialgleichung erster Ordnung. „Erster Ordnung“ rührt daher, dass die höchste Ableitung, die in unserer Differentialgleichung vorhanden ist, der ersten Ableitung, in unserem Fall der der Spannung, entspricht! R und C sind Konstanten oder konstante Koeffizienten. Wie Du die Lösung dieser Art von Differentialgleichung ermitteln kannst, zeigen wir Dir im Video zu Linearen Differentialgleichungen.
Sprungantwort
Unsere Ausgangsspannung ist somit unsere gemessene Antwort des Systems auf die Erregung durch einen Spannungssprung, die sogenannte Sprungantwort. Das Schaubild des Ausgangssignals zeigt Dir, dass sich dieses Netzwerk wie ein Verzögerungsglied erster Ordnung, ein PT1-Glied, verhält. Dieses lernst Du in unserem Video zu Zusammengesetzten Übertragungsgliedern kennen. Die Gleichung für dessen Sprungantwort lautet allgemein:
Geben wir nun einen Spannungssprung u_0 in unser System und regen es dadurch an, erhalten wir für unsere gesuchte Spannung am Kondensator:
Schaltest Du die Ausgangsspannung im Zeitpunkt t=0 mit 
= 5 V ein, so schwingt sich die Ausgangsspannung für ein Netzwerk mit einem Widerstand von 5 kΩ und einer Kapazität von 4 nF folgendermaßen ein:
Hier siehst Du wie sich das Eingangssignal nach Eingabe des Spannungssprungs verhält.
Super, Mission erfüllt! Du hast es geschafft, ein System anhand einer Differentialgleichung zu beschreiben!