Beschreibung durch den Frequenzgang
Herzlich willkommen zum ersten Video dieser Playlist! Hier kannst Du deinen Wissenstank weiter füllen und Systeme näher betrachten!
Inhaltsübersicht
Systembeschreibung im Frequenzbereich
Nachdem du Systeme bereits durch Blockschaltbilder und Differentialgleichungen beschrieben hast, nimmst du sie jetzt unter einem weiteren Aspekt unter die Lupe. Im sogenannten Frequenzbereich beschreibt man ein System durch den Frequenzgang. Anders als die bisherigen Kennfunktionen, hängt der Frequenzgang jetzt nicht von der Zeit, sondern von der Kreisfrequenz ab!Als Fundament dazu dient dir die Betrachtung sinusförmiger Eingangsgrößen, beziehungsweise Testfunktionen, im Zusammenhang mit deren Antwortfunktionen. Dabei befinden sich die Antwortfunktionen im eingeschwungenen Zustand. Das Anlaufen lassen wir also beiseite. Schwingungen, die eine Sinusform besitzen, bezeichnet man als harmonisch.
Und genau so ein harmonisches Signal nimmst Du her, um ein System anzuregen. Das lässt sich in komplexer Schreibweise ausdrücken durch:


 nennt man komplexe Amplitude und ω ist die Kreisfrequenz.
nennt man komplexe Amplitude und ω ist die Kreisfrequenz.
Ausgangssignal und Frequenzgang
Als Reaktion des Systems nach der Eingabe und dem Einschwingen eines solchen u(t) erhält man ebenfalls ein harmonisches Signal. Im Vergleich zum Eingangssignal ist dieses allerdings um die Phasendifferenz φ(ω) verschoben.
Für das Ausgangssignal y(t) lautet die komplexe Schreibweise:

A (ω) ist das Verhältnis der Aus- und Eingangsamplituden. Nachdem wir Ein- und Ausgangsschreibweisen geklärt haben, definieren wir den Frequenzgang G(jω):

Damit gilt für den Systemausgang y(t) nach einer Anregung u(t) mit einem harmonischen Signal:
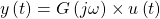
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Frequenzgang im Bildbereich
Diese Zusammenhänge haben wir gerade im Zeitbereich aufgestellt. Möchten wir den Frequenzgang im Bildbereich bestimmen, so ist dies anhand der Übertragungsfunktion G(s) möglich, die dir bereits in unserer Übung zum PT2-Glied begegnet ist. Dafür ersetzt man das s in der Übertragungsfunktion durch jω.

Mit diesen Formeln hast Du gleich eine Menge Handwerkszeug erlernt, das dich durch vielen Bereiche der Regelungstechnik begleiten wird.

