Video

Quiz

Erzwungene Konvektion – durchströmte Rohrleitung

Du wolltest schon immer verstehen, was die erzwungene Konvektion bedeutet und wie die laminare und turbulente Strömung funktionieren? Dann bist du hier genau richtig! In diesem Beitrag erfährst du alles rund ums Thema erzwungene Konvektion.

Inhaltsübersicht

Erzwungene Konvektion, laminare und turbulente Strömung anhand von Beispielen erklärt

Anhand eines Heizkörpers kann man die erzwungene Konvektion ganz einfach erklären. Der Grundmechanismus eines Heizsystems ist dir bestimmt bekannt. Es gibt einen Heizkessel, der das Wasser aufwärmt und eine Pumpe, die anschließend dieses warme Wasser durch Rohre zur Heizung befördert. Durch den Heizkörper selbst sind die Rohre schlaufenförmig verlegt, damit die Fläche, die die Wärme abgibt, größer wird. Am Ende läuft das Wasser wieder zurück zum Heizkessel und der Kreislauf beginnt von vorne. Die erzwungene Konvektion sorgt dafür, dass du außen an der Heizung deine Füße wärmen kannst. Wie du weißt, ist die Konvektion die Wärmeübertragung von einem Fluid oder Gas auf einen Körper oder anders herum. Aber was hat es mit dieser erzwungenen Konvektion auf sich?

Erzwungene Konvektion, laminare Strömung, turbulente Strömung — Grundmechanismus Heizsystem

Erzwungene Konvektion – 3 Fälle

Erzwungene Konvektion bedeutet, dass sich das Fluid oder Gas, das sich bewegt, nicht von selbst fließt bzw. strömt, sondern von außen angetrieben wird, zum Beispiel mit einer Pumpe oder einem Gebläse. Wenn du die Wärmeübertragung bzw. die erzwungene Konvektion bestimmen willst, musst du diese noch einmal in drei Fälle unterteilen:

Erzwungene Konvektion, laminare Strömung, turbulente Strömung — Erzwungene Konvektion – 3 Fälle

Die ersten beiden werden nachfolgend anhand von Beispielen anschaulich erklärt. Da in unserem Beispiel das warme Wasser mit einer Pumpe angetrieben wird und durch Rohre fließt, haben wir den ersten Fall der erzwungenen Konvektion.

Reynoldszahl berechnen

Du hast bestimmt schon die dimensionslosen Kennzahlen kennengelernt, die du jetzt wieder brauchst, um die Wärmeübertragung berechnen zu können. Die Zahl, die du gleich am Anfang benötigst, ist die Reynoldszahl. Da du noch unterscheiden musst, um welche Strömung es sich handelt, musst du zuerst die Reynoldszahl mit $Re=\frac{\omega\ast d}{\nu}$ berechnen. 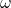Noch einmal zur Erinnerung: $\nu$ ist die kinematische Viskosität des Fluides und $\omega$ die mittlere Rohrgeschwindigkeit, die du hier berechnest mit:

$\omega=\frac{4\ast m}{\rho\ast\pi\ast d^2}$

Erzwungene Konvektion, laminare Strömung, turbulente Strömung — Reynoldszahl berechnen

Mit ist jeweils der Rohrinnendurchmesser gemeint und mit $\rho$ die Dichte des Fluides. Was $\dot{m}$ ist? Das ist der Massenstrom, der angibt, wie viel Kilogramm pro Sekunde einen bestimmten Querschnitt durchfließen. Wenn du also deine Reynoldszahl berechnet hast, können wir nun unsere Strömungsart bestimmen.

Laminare und turbulente Strömung

Zuvor erklären wir dir aber noch, welche Hauptströmungsarten es überhaupt gibt. Dazu haben wir hier zwei Skizzen:

Erzwungene Konvektion, laminare Strömung, turbulente Strömung — Laminare und turbulente Strömung

Auf dem ersten Bild siehst du eine laminare Strömung. Diese umströmt den Köper ohne Verwirbelungen. Die turbulente Strömung dagegen verläuft nicht so schön gleichmäßig, denn dort treten mehrere Verwirbelungen auf. Diese entstehen, weil die Strömung an der Kugeloberfläche, zum Beispiel durch ihre Rauheit, ein klein wenig abgebremst wird, wohingegen die oberen Schichten schneller fließen. Grund dafür können zum Beispiel auch scharfe Kanten bei Platten sein.

Da du nun das Wichtigste zu den Strömungsarten weißt, kommen wir jetzt zur Unterscheidung von laminarer Strömung und turbulenter Strömung.

Zur Einteilung hilft dir nun die kritische Reynoldszahl, die beim durchströmten Rohr bei 2.300 liegt. Ist dein berechnetes $Re\le2300$ , handelt es sich um eine laminare Strömung. Bei Re>10000 handelt es sich um eine turbulente Strömung. Wenn Re zwischen 2.300 und 10.000 liegt, also $2300\le Re\le10000$ , dann handelt es sich um eine Strömung im Übergangsbereich. Damit ist der Bereich gemeint, bei dem die laminare Strömung in die turbulente Strömung übergeht. Die Unterteilung brauchst du, da für jede Strömungsart die Nusselt-Zahl anders berechnet wird.

Erzwungene Konvektion, laminare Strömung, turbulente Strömung — Strömungsarten und Reynoldszahl

Bei laminarer Strömung rechnest du am Rohranfang mit der Formel:

${\rm Nu}_{lam},_{A}\ =\ [49,73+(1,615\ast(Pe\frac{d}{L})^\frac{1}{3}-0,7)^3+((\frac{2}{1+22Pr})^\frac{1}{6}\ast(Pe\frac{d}{L})^\frac{1}{2})^3]^\frac{1}{3}$

und nach der Anlaufstrecke mit der Formel:

${\rm Nu}_{lam},_{NA}\ =[49,73+(1,615\ast(Pe\frac{d}{L})^\frac{1}{3}-0,7)^3]^\frac{1}{3}$

Dabei ist mit die Rohrlänge gemeint, mit die Peclet-Zahl und mit die Prandtl-Zahl, die du sicherlich schon beide kennst.

Im turbulenten Bereich lautet die Formel für voll turbulente Strömung:

${\rm Nu}_{turb},_{V}\ =\ \frac{\frac{\zeta}{8}\ast Re\ast Pr}{1+12,7\ast\sqrt{\frac{\zeta}{8}}\ast({Pr}^\frac{2}{3}-1)}\ast[1+(\frac{d}{L})^\frac{2}{3}]$

und für turbulente Strömung mit Einschluss des Übergangsbereichs:

Erzwungene Konvektion, laminare Strömung, turbulente Strömung — Turbulente Strömung – Übergangsbereich

$\zeta$ ist der Druckverlustbeiwert und wird im voll turbulenten Bereich mit:

${\zeta\ =\ (1,8\ast\log_{10}(Re)-1,5)}^{-2}$

und bei turbulenter Strömung im Übergangsbereich mit:

${\zeta\ =\ (0,79\ast\ln(Re)-1,64)}^{-2}$

bestimmt. Bei der Strömung im Übergangsbereich von laminar zu turbulent, wird die Nusselt-Zahl mit dieser Formel berechnet:

${\rm Nu}_{LT}\ =\ ((1-\gamma)\ast\ {\rm Nu}_{lam},_{A}+\gamma\ast {\rm Nu}_{turb},_{V})$

Erzwungene Konvektion, laminare Strömung, turbulente Strömung — Strömung im Übergangsbereich – Nusselt-Zahl

Wie du siehst, musst du in diesem Fall sowohl die Nusselt-Zahl für die laminare Strömung als auch die für die turbulente Strömung berechnen. Der Intermittenzfaktor $\gamma$ gewichtet den Einfluss der jeweiligen Gleichungen auf das Gesamtergebnis und lässt sich bestimmen mit:

$\gamma\ =\frac{Re-2300}{{10}^4-2300}$

Erzwungene Konvektion – Nusselt-Zahl und Korrekturfaktor

So, jetzt hast du zwar schon das Schlimmste hinter dir, aber wir sind leider noch nicht ganz fertig. Jedoch keine Angst, das ist nicht so schwer. Um den Wärmeübergang richtig bestimmen zu können, musst du dir vorher noch überlegen, ob du den Richtungseinfluss berücksichtigst oder nicht. Deine gerade eben ermittelte Nusselt-Zahl muss nämlich noch mit dem Korrekturfaktor K_T multipliziert und somit korrigiert werden, damit du ein wahres Ergebnis erhältst. Die Formel lautet also:

${\rm Nu}_K=\ Nu\ast K_{T}$

K_T berechnest du bei Flüssigkeiten mit:

$K_{t},_{l}\ =(\frac{Pr}{\Pr_w})^{0,11}$

Erzwungene Konvektion, laminare Strömung, turbulente Strömung — Richtungseinfluss und Korrekturfaktor

$\Pr_W$ ist die Prandtl-Zahl bei Wandtemperatur T_W . Mit „nur Pr“ ist die Prandtl-Zahl bei Bezugstemperatur gemeint. Da bei uns der Körper durchströmt wird, lautet die Formel:

$T_{bez}\ =\ \frac{T_A+T_E}{2}$

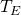wobei T_A die Temperatur am Austritt und T_E die Temperatur am Eintritt beschreibt.

Den Korrekturfaktor für Gase berechnest du mit der Formel:

$K_{T},_{g}=(\frac{T_{bez}}{T_w})^n$

Der Exponent ist für turbulente und laminare Strömung wieder unterschiedlich. Bei laminarer Strömung ist n=0 und bei turbulenter ist n=0, wenn $\frac{T_{bez}}{T_{w}}>1,0$ und n=0,45, wenn $0,5<\frac{T_{bez}}{T_w}<1,0$ .

Wenn du den Richtungseinfluss unberücksichtigt lässt, wird K_T einfach zu 1.

Erzwungene Konvektion, laminare Strömung, turbulente Strömung — Korrekturfaktor Gase

Da du nun deine korrigierte Nusselt-Zahl hast, sind wir auch schon fast am Ende. Wie du sicherlich bereits weißt, ist:

$Nu\ =\frac{\alpha\ast L}{\lambda}$

Da wir den Wärmeübergang berechnen wollen, musst du noch nach dem Wärmeübergangskoeffizienten $\alpha$ auflösen. Du erhältst also die Formel:

$\alpha=\frac{Nu\ast\lambda}{L}$

Erzwungene Konvektion, laminare Strömung, turbulente Strömung — Wärmeübergang berechnen

Für setzt du deine – der Strömungsart entsprechend berechnete und korrigierte – Zahl ${\rm Nu}_K$ ein. Da $\lambda$ als Stoffgröße und bekannt sind, kannst du damit deinen Wärmeübergang berechnen.

Erzwungene Konvektion – längsumströmte, ebene Platte

Was die erzwungene Konvektion mit einer Heizung zu tun hat, weißt du bereits und auch mit den Begriffen laminare Strömung und turbulente Strömung kannst du etwas anfangen. Du weißt aber sicherlich auch, dass ein fahrendes Auto einen Luftwiderstand erfährt und deshalb auch von Luft umströmt wird. Wenn der Luftstrom warm ist, kann an der Oberfläche des Autos erzwungene Konvektion stattfinden, also ein Wärmeübergang von der warmen Luft auf deine kühlere Autooberfläche.

Erzwungene Konvektion, laminare Strömung, turbulente Strömung — Konvektion – beispielhafte Darstellung

Und genau das ist der Grund, wieso sich dein Auto erwärmt. Da das Auto angetrieben wird, fällt der Wärmeübergang hier in den Bereich der erzwungenen Konvektion. Um die erzwungene Konvektion berechnen zu können, betrachten wir die Kontur des Autos vereinfacht als eine ebene Platte.

Wir brauchen auch hier wieder die dimensionslosen Kennzahlen, um am Ende über die Nusselt-Zahl zum Wärmeübergang zu kommen.

Laminare und turbulente Strömung

Zuerst einmal musst du wieder die Reynoldszahl berechnen, um deine Strömungsart herauszufinden. Dabei ist dieses Mal 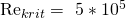${\rm Re}_{krit}=\ 5\ast10^5$ . Ist dein berechneter Wert $Re\le5\ast10^5$ , handelt es sich um eine laminare Strömung. Wenn $Re>5\ast10^5$ ist, dann haben wir eine turbulente Strömung vorliegen. Auch hier gibt es eine Art Übergangsbereich. Wenn die Platte so gestaltet ist, dass die Vorderkante günstig gestaltet ist, also nicht stumpf ist, dann haben wir eine turbulente Grenzschicht mit laminarem Anlauf. Das bedeutet, dass wir am Anfang eine laminare Strömung haben, die dann zu einer turbulenten Strömung wird. Dabei gilt 10<Re<10^7 . Die Reynoldszahl berechnest du mit:

$Re=\frac{\omega\ast L}{\nu}$

Erzwungene Konvektion, laminare Strömung, turbulente Strömung — Laminare Strömung und turbulente Strömung – Reynoldszahl berechnen

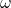Dabei ist $\nu$ wieder die kinematische Viskosität. ist hier die Plattenlänge und $\omega$ die Anströmgeschwindigkeit, also in unserem Beispiel die Geschwindigkeit, mit dem das Auto fährt, vorausgesetzt es geht kein Wind.

Wenn du deine Strömungsart bestimmt hast, kannst du die Nusselt-Zahl ausrechnen. Die Formel für die laminare Strömung lautet:

${\rm Nu}_{lam}=0,664\ast\sqrt{Re}\ast\sqrt[3]{Pr}$

Bei turbulenter Strömung berechnest du deine Nusselt-Zahl mit:

${\rm Nu}_{tur}=\frac{0,037\ast{Re}^{0,8}\ast Pr}{1+2,443\ast{Re}^{-0,1}\ast({Pr}^\frac{2}{3}-1)}$

Erzwungene Konvektion, laminare Strömung, turbulente Strömung — Strömungsart bestimmen und Nusselt-Zahl berechnen

Um den Nu-Wert mit laminarem Anlauf bestimmen zu können, brauchst du wieder sowohl die Nusselt-Zahl aus der laminaren Strömung als auch die aus der turbulenten Strömung. Du rechnest also mit:

$Nu=\sqrt{{{\rm Nu}_{lam}}^2+{{\rm Nu}_{turb}}^2}$

Quiz zum Thema Erzwungene Konvektion - Durchströmte Rohrleitung

Erzwungene Konvektion – Nusselt-Zahl und Korrekturfaktor

Du wirst dir bestimmt denken können, dass wir auch hier die Nusselt-Zahl wieder korrigieren müssen. Dazu brauchst du den Korrekturfaktor K_T , der den Richtungseinfluss des Wärmestroms mitberücksichtigt. Für Flüssigkeiten berechnest du den Korrekturfaktor mit:

$K_{t},_{l}}\ =\ (\frac{Pr}{Pr_w})^{0,25}$

und für Gase mit:

$K_{T},_{g}=\ (\frac{T_{bez}}{T_w})^{0,12}$

Erzwungene Konvektion, laminare Strömung, turbulente Strömung — Korrekturfaktor berechnen

Zur Erinnerung: $\Pr_W$ ist die Prandtl-Zahl bei Wandtemperatur T_W und „nur Pr“ die Prandtl-Zahl bei Bezugstemperatur. Da dieses Mal der Körper umströmt wird, berechnest du die Bezugstemperatur mit:

${T}_{bez}=\frac{T_w+T_\infty}{2}$

Mit deiner korrigierten Nusselt-Zahl 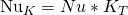${\rm Nu}_K=Nu\ast K_T$ kannst du dann deinen Wärmeübergangskoeffizienten bestimmen. Da auch in diesem Modell $Nu\ =\frac{\alpha\ast L}{\lambda}$ gilt, lautet die umgestellte Formel:

$\alpha=\frac{Nu\ast\lambda}{L}$

Erzwungene Konvektion, laminare Strömung, turbulente Strömung — Wärmeübergangskoeffizient berechnen

So, jetzt haben wir es geschafft. Nun kennst du dich bei der erzwungenen Konvektion bestens aus und weißt, was die laminare Strömung und die turbulente Strömung sind.

zur Videoseite: Erzwungene Konvektion - Durchströmte Rohrleitung

Beliebte Inhalte aus dem Bereich Wärmelehre

Konvektiver Wärmeübergang

Erzwungene Konvektion - Durchströmte Rohrleitung

Erzwungene Konvektion - längsumströmte, ebene Platte

Erzwungene Konvektion - Querumströmter Körper

Natürliche Konvektion

Hallo, leider nutzt du einen AdBlocker.

Auf Studyflix bieten wir dir kostenlos hochwertige Bildung an. Dies können wir nur durch die Unterstützung unserer Werbepartner tun.

Schalte bitte deinen Adblocker für Studyflix aus oder füge uns zu deinen Ausnahmen hinzu. Das tut dir nicht weh und hilft uns weiter.

Danke!
Dein Studyflix-Team

Wenn du nicht weißt, wie du deinen Adblocker deaktivierst oder Studyflix zu den Ausnahmen hinzufügst, findest du hier eine kurze Anleitung. Bitte .