Erzwungene Konvektion – Querumströmter Körper
Wenn du nach einer kalten Dusche deine Haare trocknen möchtest, machst du das meistens mit einem Föhn. Wie dieser funktioniert, erklären wir dir in diesem Video.
Inhaltsübersicht
Übertragung der Wärme der Drähte an die Luft
Die Luft, die aus der Umgebung angezogen wird, wird wiederum über die warmen Heizdrähte geleitet. Die Luft erwärmt sich dabei und kommt vorne als warmes Gebläse, mit dem du dir deine Haare föhnst, heraus.
Jetzt wirst du dich sicher fragen, wieso die Luft warm wird, wenn sie über die Heizdrähte strömt. Das liegt an der Konvektion. Die Wärme wird vom Draht an die Luft weitergleitet. Da hier die Luft mithilfe eines Ventilators bewegt wird, handelt es sich um die erzwungene Konvektion. Wenn du jetzt genau wissen willst, wie viel beziehungsweise wie gut die Wärme übergeben wird, musst du das über die Nußelt-Zahl machen.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Unterschied bei der Berechnung querumströmter Körper
Da die Heizdrähte dieses Mal nicht durchströmt oder der Länge nach umströmt werden, handelt es sich hier um den Fall von querumströmten Körpern. Hierbei brauchst du die dimensionslosen Kennzahlen. Doch zuvor wollen wir noch zwischen zwei verschiedenen Arten unterscheiden. Zum einen gibt es Körper wie beispielsweise Zylinder, Kugel und Platte und zum anderen ein ganzes Rohrbündel. Den Wärmeübergangskoeffizienten bestimmst du je nach Art anders.
Fangen wir mit den Körpern Zylinder, Kugel und Platte an. Hier benötigst du wieder die Reynolds-Zahl. Diese lässt sich berechnen mit  .
.
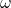 ist die Anströmgeschwindigkeit, also die Geschwindigkeit mit der der Ventilator die Luft über die Heizdrähte treibt. L‘ ist die Überstromlänge, die je nach Körper unterschiedlich ist.
ist die Anströmgeschwindigkeit, also die Geschwindigkeit mit der der Ventilator die Luft über die Heizdrähte treibt. L‘ ist die Überstromlänge, die je nach Körper unterschiedlich ist.
Beim Zylinder ist  , wobei d der Außendurchmesser ist. Bei der Kugel ist L‘=d, also der Kugeldurchmesser. Bei der Platte ist L‘=L, also die Plattenlänge.
, wobei d der Außendurchmesser ist. Bei der Kugel ist L‘=d, also der Kugeldurchmesser. Bei der Platte ist L‘=L, also die Plattenlänge.
Dein Re brauchst du, um die Nußelt-Zahl berechnen zu können. Die Formel für diese mittlere Nußelt-Zahl lautet  .
.
Die Werte für  beziehen sich auf die Oberfläche, also auf die Art des Körpers. Du kannst sie einer Tabelle entnehmen, die dir in der Klausur meist gegeben ist.
beziehen sich auf die Oberfläche, also auf die Art des Körpers. Du kannst sie einer Tabelle entnehmen, die dir in der Klausur meist gegeben ist.
Für den Zylinder ist Nuo=0,3, für die Kugel ist Nuo=2 und für die Platte ist Nuo=0.
Deine laminare Nußelt-Zahl berechnest du mit ![Rendered by QuickLaTeX.com {Nu}_{lam}= 0,664*\sqrt{ReL\prime}\ * \sqrt[3]{Pr}](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-46e17bb110f30dc7d00c4382d80e2a7b_l3.png) .
.
Dein ReL‘ hast du ja bereits ermittelt und du weißt aus den letzten Videos auch schon, dass die Prandtl-Zahl  ist. Die turbulente Nußelt-Zahl hingegen berechnest du mit:
ist. Die turbulente Nußelt-Zahl hingegen berechnest du mit:  .
.
Berücksichtigung des Korrekturfaktors für den Richtungsfluss
Dir ist sicher schon aufgefallen, dass der Korrekturfaktor, der den Richtungseinfluss berücksichtigt, bei der mittleren Nußelt-Zahl mit einbezogen worden ist. Berechnen musst du diesen für Flüssigkeiten mit  und für Gase mit
und für Gase mit  .
.
 ist dabei die Prandtl-Zahl bei Wandtemperatur
ist dabei die Prandtl-Zahl bei Wandtemperatur  .
.
 bekommst du wieder aus
bekommst du wieder aus  . Da du aber ja den Wärmeübergang bestimmen willst, musst du noch die Formel
. Da du aber ja den Wärmeübergang bestimmen willst, musst du noch die Formel  nach
nach  umstellen.
umstellen.
Die umgestellte Formel lautet dann  .
.
Anwendung des Rohrbündelmodells
So, jetzt kannst du für Zylinder, Kugeln und Platten den Wärmeübergang bestimmen.
Beim Föhn ist es aber eher so, dass die Heizdrähte hintereinander in einem Haufen liegen. Deswegen musst du beim Föhn das Modell der Rohrbündel betrachten.
Hier siehst du eine Skizze dazu. Darin kannst du eine fluchtende Anordnung, bei der die Rohre in einer Reihe direkt hintereinander angeordnet sind, und eine versetzte Anordnung erkennen. Dort ist jede zweite Spalte leicht versetzt. Die Anordnung musst du berücksichtigen, da sonst das Ergebnis verfälscht wird.
Aber schauen wir uns zuerst die Reynolds-Zahl an. Die Re-Zahl bezieht sich diesmal auf den Hohlraum zwischen den einzelnen Rohren und wird berechnet mit 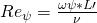 .
.
L‘ ist die Überströmlänge, die beim Rohrbündel mit  berechnet wird.
berechnet wird.
 ist die Hohlraumgeschwindigkeit, also die Geschwindigkeit, die das Medium zwischen den einzelnen Rohren hat und wird bestimmt mit
ist die Hohlraumgeschwindigkeit, also die Geschwindigkeit, die das Medium zwischen den einzelnen Rohren hat und wird bestimmt mit  .
.
 ist der Hohlraumanteil und hängt vom Längenverhältnis b und dem Querteilverhältnis a ab.
ist der Hohlraumanteil und hängt vom Längenverhältnis b und dem Querteilverhältnis a ab.
Mit  und
und  ergibt sich für den Fall, dass b<1 ist, für
ergibt sich für den Fall, dass b<1 ist, für  .
.
Für den Fall, dass b≥1 ist, ist  . Jetzt hast du endlich alle Größen, um die Re-Zahl berechnen zu können.
. Jetzt hast du endlich alle Größen, um die Re-Zahl berechnen zu können.
Nu-Zahl und Rohranordnungsfaktor
Nun brauchen wir die mittlere Nu-Zahl. Die Formel dafür lautet:

N ist dabei die Anzahl der Rohre, aus dem dein Rohrbündel besteht. Deine laminare und turbulente Nußelt-Zahl berechnest du genauso wie gerade eben beim einfachen Zylinder nur eben mit deinem neuen  . Es ist also:
. Es ist also:
![Rendered by QuickLaTeX.com {Nu}_{lam} = 0,664*\sqrt{Re\psi}\ * \sqrt[3]{Pr}](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-f08e476a22e73569ada49d8a605b4405_l3.png) und
und  .
.
Du fragst dich sicher, was dann noch dieses fA in der Formel ist. Das ist der sogenannte Rohranordnungsfaktor, der eben wie der Name schon sagt, die Rohranordnung berücksichtigt. Für die fluchtende Anordnung gilt:
 .
.
Für die versetzte Anordnung lautet die Formel:
 .
.
Bestimmung des Wärmeübergangs 
So, jetzt brauchst du nur noch den richtigen Korrekturfaktor und du kannst deine Nu-Zahl komplett bestimmen. Die Formeln sind fast dieselben, wie vorher bei den Einzelkörpern mit  für Flüssigkeiten und
für Flüssigkeiten und  für Gase. Dabei ist p = 0,25 wenn
für Gase. Dabei ist p = 0,25 wenn  und p = 0,11 wenn
und p = 0,11 wenn  .
.
Der Exponent n ist gasabhängig, denn bei Stickstoff  ist n=0,12 und bei allen anderen Gasen ist n=0.
ist n=0,12 und bei allen anderen Gasen ist n=0.
Gleich hast du es geschafft. Denn da du ja jetzt deine Nu-Zahl weißt, kannst du deinen Wärmeübergang mit  bestimmen.
bestimmen.
Wenn du dir also das nächste Mal deine Haare trocken föhnst, weißt du bestens über den Vorgang Bescheid. Viel Erfolg beim Berechnen!









