Stefan Boltzmann Gesetz
Wie du mit dem Stefan Boltzmann Gesetz die thermisch abgestrahlte Leistung von idealen schwarzen Körpern berechnen kannst, zeigen wir dir in diesem Beitrag. Zunächst leiten wir das Stefan Boltzmann Gesetz über die Thermodynamik und auch über die Quantenmechanik her, um dir dann im Anschluss in einem Rechenbeispiel die Anwendung näher zu bringen.
Du möchtest in kurzer Zeit das Stefan Boltzmann Gesetz verstehen und anwenden können? Dann ist unser Video genau das richtige für dich!
Inhaltsübersicht
Stefan Boltzmann Gesetz einfach erklärt
Besitzt ein Körper eine Temperatur über null Kelvin, so sendet dieser Wärmestrahlung aus.
Ein solcher Körper absorbiert, im Gegensatz zu realen Körpern, alle elektromagnetische Strahlung die auf ihn trifft. Außerdem ist seine Wärmestrahlung, welche er in Form elektromagnetischer Strahlung aussendet, unabhängig von der Beschaffenheit des Körpers.
Stefan Boltzmann Gesetz Formel
Das Stefan-Boltzmann-Gesetz ist nach dem Physiker Josef Stefan (1835-1893) und dem Physiker Ludwig Boltzmann (1844-1906) benannt. Dieses Gesetz stellt einen Zusammenhang zwischen der Strahlungsleistung  , der Fläche des schwarzen Körpers
, der Fläche des schwarzen Körpers  und der Temperatur
und der Temperatur  auf
auf

Die Proportionalitätskonstante  heißt Stefan Boltzmann Konstante und hat einen Wert von
heißt Stefan Boltzmann Konstante und hat einen Wert von

Da das Gesetz proportional zur vierten Potenz der Temperatur ist, wird es auch als „Boltzmannsches T hoch 4 Gesetz“ bezeichnet.
Wichtig zu erwähnen ist, dass die Stefan Boltzmann Konstante nicht mit der Boltzmann Konstante  verwechselt werden darf, welche eine Naturkonstante darstellt.
verwechselt werden darf, welche eine Naturkonstante darstellt.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Stefan Boltzmann Gesetz Herleitung aus der Thermodynamik
Möchte man das Stefan-Boltzmann Gesetz aus der Thermodynamik ableiten, so startet man mit der Fundamentalgleichung der Thermodynamik , welche für ein abgeschlossenes System im thermodynamischen Gleichgewicht gilt

Hierbei ist  die Entropie
,
die Entropie
,  die innere Energie,
die innere Energie,  das Volumen und
das Volumen und  der Druck. Da
der Druck. Da  ,
,  und
und  totale Differentiale sind, kann diese Gleichung mit den Integrabilitätsbedingungen zu folgender Gleichung umgeformt werden
totale Differentiale sind, kann diese Gleichung mit den Integrabilitätsbedingungen zu folgender Gleichung umgeformt werden
(1)  .
.
Für den Zusammanhang von der Energiedichte 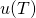 und dem Strahlungsdruck
und dem Strahlungsdruck  eines schwarzen Körpers gilt die Beziehung
eines schwarzen Körpers gilt die Beziehung

Desweiteren kann die innere Energie eines schwarzen Körpers mit der Formel
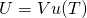
berechnet werden. Woraus folgt, dass

Setzt man das in die obere Gleichung (1) ein, dann erhält man


Integrieren und in die Formel für die innere Energie  einsetzen, liefert dann für die Energiedichte
einsetzen, liefert dann für die Energiedichte

beziehungsweise für die innere Energie

Hierbei ist  eine Konstante, welche damals zuerst aus Experimenten bestimmt wurde und später auf Naturkonstanten zurückgeführt werden konnte
eine Konstante, welche damals zuerst aus Experimenten bestimmt wurde und später auf Naturkonstanten zurückgeführt werden konnte

wobei  die Lichtgeschwindigkeit repräsentiert. Multiplizierst du nun die Energiedichte
die Lichtgeschwindigkeit repräsentiert. Multiplizierst du nun die Energiedichte 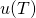 mit
mit  , dann erhältst du die Strahlungsleistung pro Flächeneinheit und somit das Stefan Boltzmann Gesetz
, dann erhältst du die Strahlungsleistung pro Flächeneinheit und somit das Stefan Boltzmann Gesetz
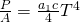

Es ist darauf hinzuweisen, dass man hierbei die Dimensionen berücksichtigen muss. Wenn eine Dimension größer ist als die relevanten Wellenlängen, so wird diese Dimension berücksichtigt und die innere Energie  wird größer. Für die innere Energien der verschiedenen Dimensionen gilt:
wird größer. Für die innere Energien der verschiedenen Dimensionen gilt:
-
1D (zum Beispiel ein Stab):
 mit der Länge
mit der Länge  ,
, -
2D (eine Fläche):
 mit der Fläche
mit der Fläche  ,
, -
3D (ein Volumen):
 mit dem Volumen
mit dem Volumen  .
.
Dabei sind die Konstanten  ,
,  und
und  gegeben durch
gegeben durch
-
 ,
, -
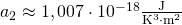 ,
, -
 .
.
Stefan Boltzmann Gesetz Herleitung aus der Quantenmechanik
Auch aus der Quantenmechanik kann das Stefan Boltzmann Gesetz abgeleitet werden. Dabei geht man von der spektralen Strahlungssdichte eines schwarzen Körpers aus und integriert diese über alle Frequenzen  und über den Halbraum
und über den Halbraum  , in den der schwarze Körper abstrahlt
, in den der schwarze Körper abstrahlt

Löst man dieses Intergral und intergriert  nochmals über die abstrahlende Fläche des schwarzen Körpers, dann führt dies auf das Stefan Boltzmann Gesetz.
nochmals über die abstrahlende Fläche des schwarzen Körpers, dann führt dies auf das Stefan Boltzmann Gesetz.
Stefan Boltzmann Gesetz Anwendungsbedingungen
Nicht-Schwarze Körper können mit dem oberen Stefan Boltzmann Gesetz nicht beschrieben werden. Besitzt ein Nicht-Schwarzer Körper jedoch einen richtungsunabhängigen Emissionsgrad  , der für alle Frequenzen denselben Wert hat, dann kann man die Strahlungsleistung mit der Formel
, der für alle Frequenzen denselben Wert hat, dann kann man die Strahlungsleistung mit der Formel

berechnen. Aufgrund der Temperaturabhängigkeit des Emissionsgrades, ist die Strahlungsleistung bei Nicht-Schwarzen Körpern nicht mehr streng proportional zu  .
.
Stefan Boltzmann Gesetz Beispiel
Mit dem Stefan Boltzmann Gesetz kann man zum Beispiel die Oberflächentemperatur der Sonne annähernd berechnen. Dabei behandelt man die Sonne näherungsweise als schwarzer Körper und kann somit die obere Formel einfach nach der Temperatur  umformen
umformen


Hierfür benötigt man jedoch die Strahlungsleistung der Sonne  . Um die Strahlungsleistung der Sonne zu berechnen, kann man auf der Erdoberfläche die Strahlungsstärke
. Um die Strahlungsleistung der Sonne zu berechnen, kann man auf der Erdoberfläche die Strahlungsstärke  messen und dann die Strahlungsleistung mit der Formel
messen und dann die Strahlungsleistung mit der Formel

bestimmen. Für die Strahlungsstärke verwenden wir in diesem Beispiel die Solarkonstante  . Dabei repräsentiert
. Dabei repräsentiert  den Abstand von der Erde zur Sonne und
den Abstand von der Erde zur Sonne und  den Raumwinkel. Wir gehen weiterhin davon aus, dass die Sonne isotrop in alle Raumrichtungen abstrahlt, weshalb der Raumwinkel dann
den Raumwinkel. Wir gehen weiterhin davon aus, dass die Sonne isotrop in alle Raumrichtungen abstrahlt, weshalb der Raumwinkel dann  beträgt. Setzt man die Strahlungsleistung in die obere Formel ein, so führt dies auf
beträgt. Setzt man die Strahlungsleistung in die obere Formel ein, so führt dies auf

Außerdem lässt sich die Oberfläche  der Sonne mit dem Radius der Sonne von
der Sonne mit dem Radius der Sonne von  einfach berechnen mit
einfach berechnen mit

Dabei gehen wir näherungsweise davon aus, dass die Oberfläche der Sonne als Kugeloberfläche betrachtet werden kann. Setzt man die Werte in die Formel ein, dann erhält man für die Temperatur der Sonnenoberfläche


