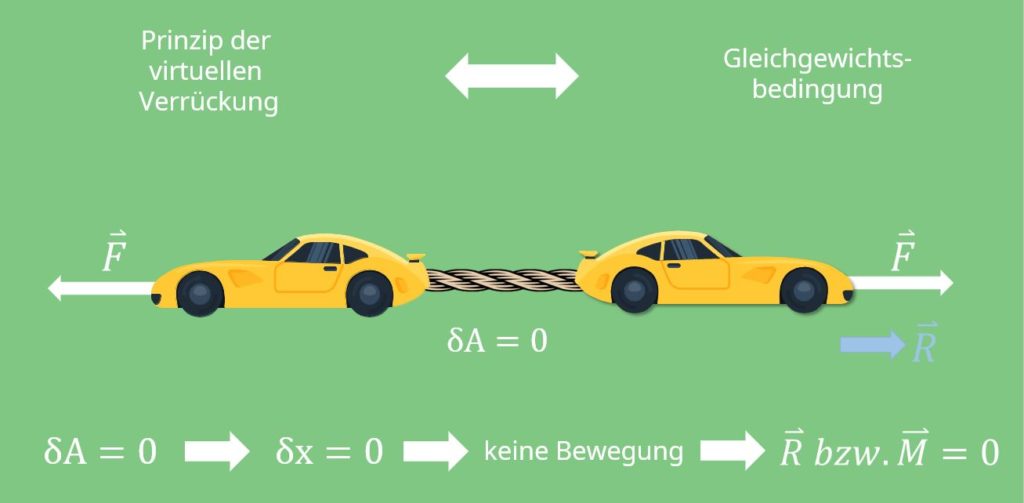
Prinzip der virtuellen Verschiebung
In diesem Artikel erklären wir dir die virtuelle Verschiebung und berechnen Beispiele. Falls du nicht viel physikalischen Text lesen möchtest, haben wir dir alles in unserem Video in kürzester Zeit aufbereitet.
Inhaltsübersicht
Virtuelle Verschiebung einfach erklärt
Die virtuelle Verschiebung wird auch oft als Prinzip der virtuellen Verrückung (PdvV) oder nur als virtuelle Verschiebung bezeichnet. Das PdvV ist einfach nur eine Alternative zur Gleichgewichtsbedingung. Über das PdvV Systeme zu berechnen, ist zum Teil einfacher und wird deshalb oft verwendet. Beim PdvV wird dazu die Arbeit, die durch Kräfte geleistet wird, betrachtet.
Virtuelle Verschiebung Definition
Das Prinzip der virtuellen Verrückung hat drei wichtige Eigenschaften:
Aus diesen Eigenschaften folgt, dass wir das PdvV für statisch unbestimmte, überbestimmte und statisch bestimmte Systeme anwenden können.
Weiterhin wird beim PdvV eine bestimme Symbolik verwendet:
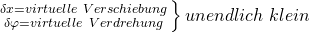
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
PdvV und mechanische Arbeit
Grundsätzlich gilt beim PdvV, dass unsere Arbeit gleich Null sein soll. Definiert wird die Arbeit in dem Fall durch  . Dieses beschreibt im Genaueren den Zuwachs der Arbeit infolge äußerer Lasten, z.B. durch irgendeine Kraft, die auf unser System wirkt. Das heißt, wir summieren die geleisteten Arbeiten infolge infinitesimaler Verschiebung und setzen diese gleich null.
. Dieses beschreibt im Genaueren den Zuwachs der Arbeit infolge äußerer Lasten, z.B. durch irgendeine Kraft, die auf unser System wirkt. Das heißt, wir summieren die geleisteten Arbeiten infolge infinitesimaler Verschiebung und setzen diese gleich null.
Das kommt dir vielleicht aus der Gleichgewichtsbedingung bekannt vor. Und tatsächlich sind die Berechnungen äquivalent zueinander. Wir können also vom PdvV auf die Gleichgewichtsbedingung schließen und andersrum. Für die Gleichgewichtsbedingungen in der Statik, haben wir dir hier einen extra Videobeitrag verlinkt.
- Wenn die Summe aller Kräfte und Momente gleich null ist, führt dies zu keiner Bewegung des Systems. Somit wird keine Arbeit verrichtet.
- Wird keine Arbeit verrichtet, kann kein Weg zurückgelegt worden sein und eine Bewegung ist ausgeschlossen. Das heißt, die resultierende Kraft und das resultierende Moment müssen null gewesen sein.
Virtuelle Verschiebung – Beispiel
Damit haben wir auch schon die Grundlagen über die virtuelle Verrückung abgehakt. Doch wie funktioniert die virtuelle Verrückung jetzt eigentlich? Allgemein gilt beim PdvV:

Um das System zu lösen, betrachten wir nun zwei Beispiele:
Als erstes schauen wir uns ein System mit einem Freiheitsgrad an: Also eine einfache Wippe, die an einem Festlager befestigt ist. Die linke Seite der Wippe hat jetzt die Länge  gleich
gleich  und die rechte Seite
und die rechte Seite  gleich
gleich  . Wir belasten nun das linke Ende mit einem Kind, das die Kraft
. Wir belasten nun das linke Ende mit einem Kind, das die Kraft  gleich
gleich  aufbringt. Welche Kraft
aufbringt. Welche Kraft  brauchen wir nun, damit keine Bewegung einsetzt?
brauchen wir nun, damit keine Bewegung einsetzt?
Geometrie
Im ersten Schritt betrachten wir die Geometrie für die virtuelle Verrückung. Das heißt, wir schauen uns an, wo unser  und unser
und unser  liegen und wie der Zusammenhang zwischen den Größen ist. Denn unser Ziel ist es ja nur eine Gleichung am Ende zur Bestimmung zu haben.
liegen und wie der Zusammenhang zwischen den Größen ist. Denn unser Ziel ist es ja nur eine Gleichung am Ende zur Bestimmung zu haben.
Mit Hilfe der Kleinwinkelnäherung finden wir dann heraus:
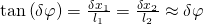
Gleichung
Als zweites stellen wir die vorhin genannte Gleichung für die virtuelle Arbeit auf und sortieren sie nach unseren Größen  und
und  . Und mit Hilfe der Geometrie haben wir am Ende dann nur noch eine der beiden Größen. So ergibt sich, dass die Terme vor unseren virtuellen Verrückungen oder unsere virtuelle Verrückung selbst gleich null sein müssen. Das heißt, man muss es einfach nur noch umformen:
. Und mit Hilfe der Geometrie haben wir am Ende dann nur noch eine der beiden Größen. So ergibt sich, dass die Terme vor unseren virtuellen Verrückungen oder unsere virtuelle Verrückung selbst gleich null sein müssen. Das heißt, man muss es einfach nur noch umformen:

Nun haben wir einen Term innerhalb der Klammer und unsere infinitesimale Verrückung. Wir setzen nun den Term in der Klammer gleich null und erhalten folgendes Ergebnis:

Setzen wir nun die Zahlenwerte ein, ergibt sich:

Wir brauchen also am anderen Ende eine Kraft von  .
.
Virtuelle Verschiebung – Beispiel II
Als zweites Beispiel nehmen wir etwas Komplexeres: Wir betrachten einen einfachen Gelenkträger und suchen eine Auflagerkraft. Unser Träger hat ein Festlager. Ganz links darauf folgt ein Loslager, auf dem unser erster Balken nur aufliegt. Danach verbindet ein Momentengelenk den ersten Balken mit dem zweiten, der wiederum mit einem weiteren Loslager befestigt ist.
Auflagerkräfte
Wir suchen jetzt nach der Auflagerkraft  unter der Belastung der Kräfte
unter der Belastung der Kräfte  gleich
gleich  ,
,  gleich
gleich  und
und  gleich
gleich  . Wir rechnen wieder erst einmal ohne konkrete Werte und setzen diese dann am Ende ein.
. Wir rechnen wieder erst einmal ohne konkrete Werte und setzen diese dann am Ende ein.
Um die Auflagerkraft des Loslagers  zu finden, müssen wir unser Auflager vorher durch eine Kraft ersetzen, damit unser System theoretisch verschiebbar wird.
zu finden, müssen wir unser Auflager vorher durch eine Kraft ersetzen, damit unser System theoretisch verschiebbar wird.
Geometrie
Zu Beginn betrachten wir wieder die Geometrie, die uns folgende Zusammenhänge liefert:

Als zweites stellen wir wieder die Gleichung für die virtuelle Arbeit auf und setzen sie gleich null. Danach formen wie mit Hilfe der Geometrie wieder so um, dass wir nur noch eine Abhängigkeit in Bezug auf die virtuelle Verrückung haben und klammern diese aus:

Im Anschluss muss wieder der Term innerhalb der Klammer gleich null sein und es ergibt sich für unsere Auflagerkraft: