Schwerpunkt berechnen
Für viele Anwendungen in der Mechanik ist es wichtig, den Schwerpunkt berechnen zu können. Falls du dir mit der Schwerpunktberechnung noch schwertust, bist du hier genau richtig. Wir erklären dir, wie du über die Infinitesimalrechnung ein Integral bildest, mit welchem du über einige Vereinfachungen schließlich den Flächenschwerpunkt berechnen kannst.
Inhaltsübersicht
Schwerpunkt berechnen einfach erklärt
Zunächst müssen wir klären, was der Schwerpunkt überhaupt ist. Definiert ist dieser als Angriffspunkt der Gewichtskraft. Die grundlegende Überlegung ist: An diesem Punkt, darf es kein Moment, also keine Drehung, resultierend aus der Gewichtskraft geben! Nehmen wir als Beispiel einen Stift: Bei diesem finden wir den Schwerpunkt intuitiv nahe der Mitte. Doch wie gehen wir bei komplexen Körper vor ? Um dieser Frage nachzugehen, schauen wir uns zunächst die Herleitung des Flächenschwerpunktes an.
Schwerpunkt berechnen über die Infinitesimalrechnung
Damit wir den Flächenschwerpunkt berechnen können, betrachte wir zunächst mit Hilfe der sogenannten Infinitesimalrechnung ein Integral, das den Punkt in der Theorie exakt beschreibt. Doch das Schwerpunkt Integral direkt zu lösen ist meistens zu aufwendig. Deshalb werden einige Annahmen und Tricks verwendet um das Ganze zu vereinfachen.
Zu Beginn machen wir zwei Annahmen, die wir in der Statik häufig aufstellen:
- Unser Körper hat eine konstante Dichte. Das heißt der Schwerpunkt ist jetzt nicht mehr von der Dichte abhängig, da diese überall gleich ist.
- Wir betrachten nur den ebenen Fall: Die z-Achse fällt also weg und unser Körper wird zu einer Fläche.
Deshalb müssen wir jetzt nur noch den Flächenschwerpunkt betrachten.
Aus diesen Annahmen heraus erkennst du sicher, dass wir nur noch die x- und y-Koordinate bestimmen müssen, um den Schwerpunkt zu finden.
Dadurch ergibt sich ein vereinfachtes Integral:

Das sieht ganz schön komplex aus, oder? Deshalb werden wir das ganze gleich einmal mit einem Trick vereinfachen: Das Integral beschreibt im Endeffekt nur die Summe über ganz kleine Stücke. Und die Gesamtfläche wiederum lässt sich ja bekanntermaßen als Summe der Einzelflächen darstellen.
Daraus ergibt sich dann ein einfacher Quotient aus zwei Summen:
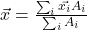
Schauen wir uns einmal den oberen Teil des Bruches an: Die meisten Formen setzen sich ja aus verschiedenen Teilen wie Rechtecken und Dreiecken zusammen. Deshalb müssen wir vorerst die betrachtete Fläche in einfachere Teilflächen, von denen wir die Schwerpunktkoordinaten kennen, aufteilen. Wenn wir nun eine Fläche haben, die sich aus Dreiecken und Rechtecken zusammensetzt, können wir diese berechnen, indem wir uns die Punkte anschauen, an denen die Schwerpunkte der Dreiecke und Rechtecke liegen. Den eines Rechtecks kannst du dir sicher selbst erschließen:
Er liegt bei jeweils der halben Seitenlänge. Wichtig ist, dass es dabei immer um den Abstand des Schwerpunkts zum gewählten ursprünglichen Koordinatensystem geht und, dass dieser dann mit der gewählten Teilfläche multipliziert werden muss.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Schwerpunkt bestimmen bei negativen Flächen
Mit dieser Formel können wir sogar für sogenannte „negative“ Flächen den Schwerpunkt berechnen. Du fragst dich, was das sein soll? Am besten schauen wir uns dazu ein Rechteck an, bei dem ein kleineres Rechteck oben rechts in der Ecke herausgeschnitten wurde. Du kannst dann einfach den Schwerpunkt des großen Rechtecks nehmen und den des kleineren davon abziehen.
Bis jetzt haben wir nur den oberen Teil des Bruches betrachtet. Der untere Teil sieht schon etwas einfacher aus. Er beschreibt die Fläche des gesamten Körpers, mit welcher wir im Folgenden den Gesamtschwerpunkt berechnen können. Beim vorhin genannten Beispiel bedeutet das, dass man die Fläche des kleineren Rechtecks von der Fläche des gesamten Rechtecks abzieht.
Bei dieser Vorgehensweise bietet es sich an das ganze erst für die x-Richtung und dann für die y-Richtung zu machen. Das heißt, du betrachtest erst den Abstand des Schwerpunkts in x-Richtung und dann in y-Richtung.
Schwerpunkt berechnen Beispiel
Jetzt wollen wir das gelernte einmal anwenden und betrachten die Schwerpunktberechnung anhand des genannten Beispiels. Dafür nehmen wir folgende Zahlenwerte an: Das große Rechteck hat die Höhe  und die Breite
und die Breite  . Das kleinere Rechteck hat die Höhe
. Das kleinere Rechteck hat die Höhe  und die Breite
und die Breite  .
.
Unser Koordinatensystem liegt jetzt genau unten links in der Ecke. Betrachten wir jetzt erst die x-Richtung: Der Schwerpunkt des großen Rechtecks in x-Richtung ist  . Der Schwerpunkt des kleinen Rechtecks liegt bei
. Der Schwerpunkt des kleinen Rechtecks liegt bei  . Jetzt brauchen wir noch die einzelnen Flächen: das große Rechteck hat die Fläche
. Jetzt brauchen wir noch die einzelnen Flächen: das große Rechteck hat die Fläche  und das kleine
und das kleine  . Jetzt setzen wir das einfach in unsere Formel ein:
. Jetzt setzen wir das einfach in unsere Formel ein:
Der Schwerpunkt liegt also in x-Richtung ungefähr  von der linken Ecke entfernt.
von der linken Ecke entfernt.
Für die y-Achse erfolgt die Rechnung genauso. Probiere das doch gleich mal selbst aus. So erhältst du dann ganz einfach den Gesamtschwerpunkt.
Zum Schluss noch ein Tipp: Versuch dir am besten die Schwerpunkte von Dreieck, Rechteck und Kreis zu merken, da diese drei Formen nicht sehr komplex sind und sich aus diesen fast alle Figuren zusammensetzen lassen.




