Reibungskoeffizient
Der Reibungskoeffizient ermöglicht dir die Reibungskraft auszurechnen. In diesem Beitrag erfährst du unter anderem wie du das machst und lernst typische Reibungskoeffizienten kennen.
Wenn du das Wichtigste zum Reibungskoeffizienten noch schneller erlernen möchtest, dann empfehlen wir dir unser Video zum Thema Reibungskoeffizient.
Inhaltsübersicht
Reibungskoeffizient einfach erklärt
Stell dir vor, du hättest einen kleinen Schrank voller Bücher, der vor dir auf dem Boden steht. Dieser Schrank wird sich nicht von der Stelle bewegen bis du ihn mit einer bestimmten Kraft anschiebst. Ist er einmal in Bewegung, dann ist die Kraft, die du für die Fortführung der Bewegung aufwenden musst, geringer als die Kraft, die du zum Anschieben brauchtest. Du kannst dir auch leicht vorstellen, dass du weniger Kraft zum Anschieben brauchst, wenn du ein paar Bücher aus dem Schrank entfernst.
Diese Beobachtung hat mit der Reibung zwischen dem Schrank und dem Boden zu tun. Die Reibungskraft, die der Boden auf den Schrank ausübt, kann mit Hilfe des Reibungskoeffizienten berechnet werden. Es wird dabei unterschieden zwischen Haftreibung und Gleitreibung.
Im Fall der Haftreibung bewegt sich der Schrank noch nicht und es gilt
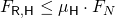 ,
,
 .
.
Hier ist  die Reibungskraft,
die Reibungskraft,  der Reibungskoeffizient im Fall der Haftreibung und
der Reibungskoeffizient im Fall der Haftreibung und  die Normalkraft.
die Normalkraft.  ist die maximale Haftreibung, die zunächst überwunden werden muss, damit sich der Schrank in Bewegung setzt.
ist die maximale Haftreibung, die zunächst überwunden werden muss, damit sich der Schrank in Bewegung setzt.
Befindet sich der Schrank in Bewegung, dann sind wir im Fall der Gleitreibung und es gilt
 .
.
Hier ist  die Reibungskraft,
die Reibungskraft,  der Reibungskoeffizient im Fall der Gleitreibung und
der Reibungskoeffizient im Fall der Gleitreibung und  die Normalkraft.
die Normalkraft.
Reibungskoeffizient Formel
In diesem Abschnitt schauen wir uns die Formeln für die Reibungskraft für beide Reibungsarten näher an und wie sich die Reibungskoeffizienten unterscheiden. Wir gehen auch kurz auf die Unterschiede beider Reibungsarten ein und inwiefern der Reibungskoeffizient hier eine Rolle spielt.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Haftreibung
Egal wie glatt eine Fläche zu scheinen mag, mikroskopisch betrachtet sind immer Unebenheiten vorhanden. Die Reibungs- und Normalkräfte entstehen durch Wechselwirkungen zwischen Molekülen zweier Flächen, die an den Unebenheiten in Kontakt kommen. Man spricht von der Haftreibung im Fall, wenn die beiden Flächen keine relative Bewegung zueinander vorweisen.
Wenn wir wieder unseren Schrank voller Bücher betrachten, dann wissen wir bereits, dass wir eine gewisse Kraft aufwenden müssen, bis sich der Schrank in Bewegung setzt. Diese Kraft entspricht gerade der maximalen Haftreibung und lässt sich wie folgt berechnen
 .
.
Hier ist  der dimensionslose Reibungskoeffizient (manchmal auch Haftreibungskoeffizient genannt).
der dimensionslose Reibungskoeffizient (manchmal auch Haftreibungskoeffizient genannt).  ist die Normalkraft in Newton (
ist die Normalkraft in Newton (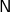 ), die vom Boden auf unseren Schrank ausgeübt wird und entspricht in diesem konkreten Beispiel gerade der Gewichtskraft
), die vom Boden auf unseren Schrank ausgeübt wird und entspricht in diesem konkreten Beispiel gerade der Gewichtskraft
 des Schrankes. Da diese maximale Kraft direkt proportional zur Normalkraft ist, und diese wiederum zum Gewicht des Schrankes, erklärt diese Formel, weswegen du weniger Kraft bräuchtest, um denselben Schrank mit weniger Büchern in Bewegung zu bringen.
des Schrankes. Da diese maximale Kraft direkt proportional zur Normalkraft ist, und diese wiederum zum Gewicht des Schrankes, erklärt diese Formel, weswegen du weniger Kraft bräuchtest, um denselben Schrank mit weniger Büchern in Bewegung zu bringen.
Solange diese maximale Kraft nicht erreicht wurde, gilt für die Kraft (auch als Haftreibungskraft bezeichnet)
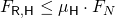 .
.
Wir sehen also, dass der Reibungskoeffizient das Verhältnis zweier Kräfte ist und somit keine Einheit besitzt. Die Gleichung der Reibungskraft ist keine vektorielle Gleichung, da die Reibungskraft immer senkrecht zur Normalkraft ist. Der Haftreibungskoeffizient  hängt von den Materialien ab, aus denen die zwei in Kontakt gekommenen Oberflächen bestehen, aber auch von der Temperatur und der Oberflächenbeschaffenheit.
hängt von den Materialien ab, aus denen die zwei in Kontakt gekommenen Oberflächen bestehen, aber auch von der Temperatur und der Oberflächenbeschaffenheit.
Gleitreibung
Schauen wir wieder unseren Schrank mit Büchern an. Wenn du jetzt den Schrank mit einer Kraft schiebst, die größer ist als die maximale Haftreibung, dann wird sich der Schrank bewegen. Dir wird auffallen, dass du zur Fortführung der Bewegung weniger Kraft als zu deren Initiierung brauchst. Das liegt daran, dass beim Eintreten der Bewegung von der Haft- zur Gleitreibung gewechselt wurde.
Im Fall der Gleitreibung gilt für die Kraft (auch als Gleitreibungskraft bezeichnet)
 .
.
Hier ist  der dimensionslose Reibungskoeffizient (manchmal auch Gleitreibungskoeffizient genannt). Auch hier ist
der dimensionslose Reibungskoeffizient (manchmal auch Gleitreibungskoeffizient genannt). Auch hier ist  die Normalkraft, die vom Boden auf den Schrank ausgeübt wird und entspricht der Gewichtskraft des Schrankes.
die Normalkraft, die vom Boden auf den Schrank ausgeübt wird und entspricht der Gewichtskraft des Schrankes.
Reibungsarten im Vergleich
Beide Reibungskräfte wirken der Richtung, in der du schiebst, entgegen. Das heißt, schiebst du den Schrank von links nach rechts, dann zeigt die Reibungskraft nach links. Umgekehrt, schiebst du den Schrank von rechts nach links, dann zeigt die Reibungskraft nach rechts.
Formal betrachtet, unterscheiden sich die beiden Reibungsarten nur im Reibungskoeffizienten. Dabei ist in der Regel der Reibungskoeffizient  für ein gegebenes Paar an Oberflächen kleiner als der entsprechende Reibungskoeffizient
für ein gegebenes Paar an Oberflächen kleiner als der entsprechende Reibungskoeffizient  . Das erklärt, weswegen du zum Starten der Bewegung mehr Kraft als zur Fortführung der Bewegung des Schrankes benötigst.
. Das erklärt, weswegen du zum Starten der Bewegung mehr Kraft als zur Fortführung der Bewegung des Schrankes benötigst.
Physikalisch betrachtet, lässt sich anhand der Namensgebung für die beiden Reibungsarten bereits der Unterschied nennen. Im Fall der Haftreibung bewegen sich die Flächen nicht zueinander, während sie sich im Fall der Gleitreibung in relativer Bewegung befinden. Während der Bewegung, werden die Bindungen, die durch die Wechselwirkungen der Moleküle an den Kontaktstellen entstehen, immer wieder neu geformt und gebrochen. Das erklärt, weswegen manchmal die Bewegung eines Körpers über eine Fläche ruckartig verlaufen kann.
Reibungskoeffizienten ausgewählter Materialien
In diesem Abschnitt findest du eine kleine Tabelle von Reibungskoeffizienten. Du solltest dir aber bewusst sein, dass der Wert des Reibungskoeffizienten nur eine Näherung ist. Zum Beispiel ist der Reibungskoeffizient zwischen Stahl und Stahl anders, wenn einer der Flächen mit Öl eingeschmiert wird. Die hier angegebenen Richtwerte der Reibungskoeffizienten beziehen sich auf den Fall, dass beide Oberflächen trocken sind.
| Oberflächen | Haftreibungskoeffizient  |
Gleitreibungskoeffizient  |
| Stahl auf Stahl | 0,2 | 0,1 |
| Stahl auf Holz | 0,5 | 0,4 |
| Stahl auf Stein | 0,8 | 0,7 |
| Stein auf Holz | 0,9 | 0,7 |
| Holz auf Holz | 0,5 | 0,4 |
| Stein auf Stein | 1,0 | 0,9 |
| Stahl auf Eis | 0,03 | 0,01 |
| Stahl auf Beton | 0,35 | 0,20 |
| Leder auf Metall | 0,6 | 0,4 |
Wenn du die Werte für die beiden Reibungskoeffizienten miteinander vergleichst, dann erkennst du, dass der Reibungskoeffizient  immer kleiner als der Reibungskoeffizient
immer kleiner als der Reibungskoeffizient  ist. Der tatsächliche Wert des Reibungskoeffizienten hängt aber von vielen Faktoren ab. Außerdem besitzt der Reibungskoeffizient keine Einheit, da er das Verhältnis zweier Kräfte beschreibt. Der Reibungskoeffizient dient nur zur Approximation, was in Realität an den Kontaktstellen zweier sich berührenden Flächen passiert.
ist. Der tatsächliche Wert des Reibungskoeffizienten hängt aber von vielen Faktoren ab. Außerdem besitzt der Reibungskoeffizient keine Einheit, da er das Verhältnis zweier Kräfte beschreibt. Der Reibungskoeffizient dient nur zur Approximation, was in Realität an den Kontaktstellen zweier sich berührenden Flächen passiert.
Reibungskoeffizient berechnen
Ordnen wir unserem Schrank mit Büchern ein paar Zahlen zu. Die Masse des Schrankes sei  , die der Bücher
, die der Bücher  . Der Reibungskoeffizient
. Der Reibungskoeffizient  zwischen dem Schrank und Boden sei
zwischen dem Schrank und Boden sei  , der Reibungskoeffizient
, der Reibungskoeffizient  gleich
gleich  . Mit welcher Kraft muss du den Schrank schieben, damit er in Bewegung kommt und welche Kraft wirkt dann nach Einsetzen der Bewegung entgegen deiner horizontalen Kraft?
. Mit welcher Kraft muss du den Schrank schieben, damit er in Bewegung kommt und welche Kraft wirkt dann nach Einsetzen der Bewegung entgegen deiner horizontalen Kraft?
Solange du am Schrank keine Kraft ausübst, ist er in Ruhe. Es herrscht also ein Gleichgewicht zwischen der Normalkraft und der Gewichtskraft
 .
.
Damit du den Schrank in Bewegung setzen kannst, musst du die maximale Haftreibung überwinden. Diese Kraft berechnet sich zu
 .
.
Hast du diese Kraft überwinden, dann bewegt sich der Schrank. Um die Bewegung fortführen zu können, musst du eine Kraft von

aufwenden. Wie erwartet, ist diese Kraft kleiner als die Kraft, die du zum Anschieben brauchtest.
Wir haben uns hier den einfachen Fall einer horizontalen Ebene angeschaut, über die sich der Schrank bewegen soll. Wir können die Situation etwas komplizierter gestalten, indem wir den Schrank auf eine schiefe Ebene stellen. Wie du in diesem Fall die Normalkraft berechnest, wird dir in unserem Artikel zum Kräfteparallelogramm gezeigt.
