Video anzeigen

Kettenregel

Wie rechnest du nach der Verkettung von Funktionen %Schlüsselwort ihre Ableitungen aus? Hier zeigen wir dir die Ableitungsregeln für zusammengesetzte Funktionen mit vielen Beispielen. % Schaue dir auch unser passendes Video dazu an!

Inhaltsübersicht

Kettenregel Ableitung

Es gibt viele Ableitungsregeln für viele verschiedene Situationen. Wenn du verkettete Funktionen oder auch zusammengesetzte Funktionen ableiten willst, brauchst du die Kettenregel. Wie schaut die Verkettung von Funktionen aus? Funktionen nennst du zusammengesetzte Funktionen, wenn du in einer Funktion für x eine zweite Funktion einsetzt (z.B. 2x in sin(x) eingesetzt ist f(x)=sin[2x]).

Kettenregel Formel

Wenn f(x) eine zusammengesetzte Funktion aus einer äußeren Funktion u(x) und einer inneren Funktion v(x) ist, brauchst du die Kettenregeln für die Ableitung:

$f(x) = \textcolor{blue}{u(}\textcolor{red}{v(x)}\textcolor{blue}{)} \quad\Rightarrow\quad f'(x) = \textcolor{teal}{u'(}\textcolor{red}{v(x)}\textcolor{teal}{)} \cdot \textcolor{orange}{v'(x)}$

Verkette Funktionen erkennst du immer daran, dass das Argument deiner Funktion komplizierter als x ist. Du leitest zum Beispiel Potenzen, Wurzeln, e-Funktionen, Logarithmen und trigonometrische Funktionen (sinus, cosinus, tangens) mit der Kettenregel ab:

$\begin{array}{lll} f(x) = \textcolor{blue}{(}\textcolor{red}{2x+1}\textcolor{blue}{)^3} & f(x) = \textcolor{blue}{\sqrt{ \textcolor{red}{x^2-3} }} & f(x) = \textcolor{blue}{\mathrm{e}^{ \textcolor{red}{5x^4} }} \\ f(x) = \textcolor{blue}{\ln( \textcolor{red}{x^2+3x-2} )} & f(x) = \textcolor{blue}{\sin(}\textcolor{red}{4x^2}\textcolor{blue}{)} \end{array}$

Kettenregel Beispiele

Schauen wir uns die Kettenregel Beispiele etwas genauer an. Aufgepasst! Manchmal brauchst du die Produkt- und Kettenregel, um Verkettung von Funktionen abzuleiten.

Beispiel 1: Ableitung Klammer

Leite die Funktion $f(x) = \textcolor{blue}{(}\textcolor{red}{2x+1}\textcolor{blue}{)^3}$ mit der Kettenregel ab. Wie gehst du vor?

Schreibe dir zuerst die Teilfunktionen heraus. Die innere Funktion ist v(x)=2x+1. Damit deine Verkettung von Funktionen f(x) gleich bleibt, muss die äußere Funktion die innere Funktion mit 3 potenzieren (f(x)=v(x)³). Deine äußere Funktion ist also u(v)=v³. Woher weißt du, welcher Teil die innere und welcher Teil die äußere Funktion ist? Wenn du deine innere Funktion v(x) wie eine Variable (z.B. x) wieder in deine äußere Funktion u(v) einsetzt (Verkettung von Funktionen), willst du die ursprüngliche Funktion f(x) wieder herausbekommen. Das nennst du Substitution und Resubstitution. Du kannst die Ableitung der Klammer jetzt berechnen, indem du die äußere Funktion und die innere Funktion getrennt ableitest. Als Nächstes kannst du dir das im Detail anschauen:

Jetzt brauchst du die Ableitungen der Teilfunktionen. Hier kannst du beide Teilfunktionen mit der Potenzregel ableiten: $(x^n)'=n\cdotx^{n-1}$ .

$\begin{array}{ll} \textcolor{red}{v(x) = 2x+1} &\Rightarrow\quad \textcolor{orange}{v'(x)=2} \\ \textcolor{blue}{u(v)=v^3} &\Rightarrow\quad\textcolor{teal}{u'(x)=3v^2} \end{array}$

Zuletzt musst du v(x), u'(v) und v'(x) nur noch in deine Kettenregel-Formel einsetzen.

$f'(x) = \textcolor{teal}{u'(\textcolor{red}{v(x)})} \cdot \textcolor{orange}{v'(x)} = \textcolor{teal}{3\cdot(\textcolor{red}{2x+1})^2}\cdot \textcolor{orange}{2} = 6\cdot(2x+1)^2$

Beispiel 2: Wurzeln ableiten

Wie wäre es mit einem zweiten Beispiel? Leite die zusammengesetzte Funktion $f(x) = \textcolor{blue}{\sqrt{ \textcolor{red}{x^2-3} }}$ mit der Kettenregel und der Wurzelregel ab.

Fange wieder mit den Teilfunktionen an. Deine äußere Funktion ist $\textcolor{blue}{u(v)=\sqrt{v}}$ und die innere Funktion ist dann $v(x) = \textcolor{red}{x^2-3}$ . Hier schreibst du deine äußere Funktion wieder mit der Variable v (Substitution), damit du sie ableiten kannst. Am Ende kannst du v dann wieder durch deine innere Funktion v(x) ersetzten (Resubstitution).

Die innere Funktion leitest du wieder mit der Potenzregel ab. Die Wurzel leitest du so ab: $\left(\sqrt{x}\right)' = \frac{1}{2\sqrt{x}}$ .

$\begin{array}{ll} \textcolor{red}{v(x)=x^2-3} &\Rightarrow\quad \textcolor{orange}{v'(x) = 2x}\\ \textcolor{blue}{u(v)=\sqrt{v}} &\Rightarrow\quad \textcolor{teal}{u'(x) = \frac{1}{2\sqrt{v}}} \end{array}$

Jetzt muss du die Teilfunktionen v(x), u'(v) und v'(x) in deine Kettenregel-Formel einsetzen.

$f'(x) = \textcolor{teal}{u'(\textcolor{red}{v(x)})} \cdot \textcolor{orange}{v'(x)} = \textcolor{teal}{\frac{1}{2\sqrt{ \textcolor{red}{x^2-3} }}} \cdot \textcolor{orange}{2x} = \frac{x}{\sqrt{x^2-3}}$

Wurzeln ableiten ist kein Problem mehr, oder?

Beispiel 3: e-Funktion ableiten

Häufig musst du auch e-Funktionen ableiten. Was ist die Kettenregel Ableitung von $f(x) = \textcolor{blue}{\mathrm{e}^{ \textcolor{red}{5x^4} }}$ ?

Der erste Schritt ist wieder die Teilfunktionen aufzuschreiben und die äußere und innere Ableitung zu berechnen. Hier ist deine äußere Funktion die e-Funktion. Du schreibst sie also wieder mit der Variable v auf: u(v) = e^v. Dann muss deine innere Funktion v(x) = 5x⁴sein. Jetzt kannst du die Exponentialfunktion wie jede andere e-Funktion ableiten. Das e-Funktion-Ableiten ist besonders einfach, die e-Funktion ändert sich nämlich nicht beim Ableiten: $\left(\mathrm{e}^v\right)'=\mathrm{e}^v$ . Auch hier ersetzt du nach dem Ableiten das v in deiner äußeren Funktion u(v) durch deine innere Funktion v(x).

$\begin{array}{ll} \textcolor{red}{v(x)=5x^4} &\Rightarrow\quad \textcolor{orange}{v'(x) = 20x^3}\\ \textcolor{blue}{u(v)=\mathrm{e}^v} &\Rightarrow\quad \textcolor{teal}{u'(v) = \mathrm{e}^v} \end{array}$

Wenn du die innere und äußere Ableitung in deine Kettenregel-Formel einsetzt, hast du die Ableitung von f(x) auch schon berechnet.

$f'(x) = \textcolor{teal}{u'(\textcolor{red}{v(x)})} \cdot \textcolor{orange}{v'(x)} = \textcolor{teal}{\mathrm{e}^{ \textcolor{red}{5x^4} }} \cdot \textcolor{orange}{20x^3} = 20x^3 \mathrm{e}^{ 5x^4 }$

Beispiel 4: ln ableiten

Du kannst jetzt die e-Funktion ableiten. Aber wie leitest du ihre Umkehrfunktion ln() ab? Schaue dir dir Funktion $f(x) = \textcolor{blue}{\ln( \textcolor{red}{x^2+3x-2} )}$ an. $\ln$ %Das sieht genauso aus wie "In", also in, kann man das noch anderweitig kennzeichnen, sodass die Verwechslungsgefahr nicht so besteht? <span style="color: #008000;">DONE</span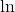> ist die Abkürzung für den natürlichen Logarithmus , aber du kannst die Kettenregel auch bei allen anderen Logarithmen benutzen.

Schreibe dir wieder deine Teilfunktionen auf: Die äußere Funktion ist der Logarithmus u(v)=ln(v) und deine innere Funktion ist v(x)=x²+3x-2. Jetzt kannst du die innere und äußere Ableitung berechnen. Du kannst die Funktion u(v) wieder wie eine Funktion mit x ableiten. Die Ableitung von natürlichen Logarithmen ist $[\ln(x)]'=\nicefrac{1}{x}$ . Für die innere Ableitung brauchst du die Potenzregel, Summenregel und Faktorregel.

$\begin{array}{ll} \textcolor{red}{v(x)=x^2+3x-2} &\Rightarrow\quad \textcolor{orange}{v'(x) = 2x+3}\\ \textcolor{blue}{u(v)=\ln(v)} &\Rightarrow\quad \textcolor{teal}{u'(v) = \frac{1}{v}} \end{array}$

Zuletzt setzt du deine innere Funktion, äußere Funktion, innere Ableitung und äußere Ableitung in deine Kettenregel-Formel ein.

$f'(x) = \textcolor{teal}{u'(\textcolor{red}{v(x)})} \cdot \textcolor{orange}{v'(x)} = \textcolor{teal}{\frac{1}{ \textcolor{red}{x^2+3x-2} }} \cdot \textcolor{orange}{(2x+3)} = \frac{2x+3}{x^2+3x-2}$

Beispiel 5: Ableitung Sinus

Häufig musst du auch trigonometrische Funktionen wie sin ableiten. Berechne die Ableitung von $f(x) = \textcolor{blue}{\sin(}\textcolor{red}{4x^2}\textcolor{blue}{)}$ !

Der erste Schritt ist wie bisher das Aufschreiben deiner Teilfunktionen. Deine äußere Funktion ist der Sinus u(v)=sin(v). Die innere Funktion v(x)=4x² ersetzt du wieder durch eine neue Variable v.

Jetzt kannst du deine Teilfunktionen ableiten. Um den sin ableiten zu können, brauchst du den Cosinus: $[\sin(x)]'=\cos(x)$ . Der Cosinus ist nämlich die Ableitung von der Sinus-Funktion. Deine innere Funktion leitest du wieder mit der Potenzregel und der Faktorregel ab: $(a\cdot x^n)' = a\cdot n\cdot x^{n-1}$ .

$\begin{array}{ll} \textcolor{red}{v(x)=4x^2} &\Rightarrow\quad \textcolor{orange}{v'(x) = 8x}\\ \textcolor{blue}{u(v)=\sin(v)} &\Rightarrow\quad \textcolor{teal}{u'(v) = \cos(v)} \end{array}$

Setzte die Ableitungen und die Teilfunktionen in deine Kettenregel-Formel ein!

$f'(x) = \textcolor{teal}{u'(\textcolor{red}{v(x)})} \cdot \textcolor{orange}{v'(x)} = \textcolor{teal}{\cos\mathopen{}\left(\textcolor{red}{4x^2}\right)\mathclose{}} \cdot \textcolor{orange}{8x} = 8x\cos\mathopen{}\left(4x^2\right)\mathclose{}$

Die Kettenregel ist gar nicht so schwer, oder?

Weitere Ableitungsregeln

Neben der Produkt- und Kettenregel Ableitung gibt es noch weitere Ableitungsregeln, mit denen du Ableitungen bestimmen kannst:

Ableitungsregel	Funktion	Ableitung
Summenregel
Differenzregel
Produktregel	$f(x)=g(x)\cdot h(x)$	$f'(x)=g'(x)\cdot h(x)+g(x)\cdot h'(x)$
Quotientenregel	$f(x)=\frac{g(x)}{h(x)}$	$f'(x)=\frac{g'(x)\cdot h(x)-g(x)\cdot h'(x)}{[h(x)]^2}$
Faktorregel	$f(x)=c\cdot h(x)$	$f'(x)=c \cdot h'(x)$
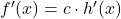Potenzregel		$f'(x)=n\cdot x^{n-1}$
Kettenregel		$f'(x)=g'(h(x))\cdot h'(x)$