Quotientenregel
Du willst wissen, wie die Ableitung mit der Quotientenregel funktioniert? Dann bist du hier genau richtig! Wenn du dich beim Lernen lieber zurücklehnst, dann schau dir doch unser Video dazu an.
Inhaltsübersicht
Quotientenregel einfach erklärt
Du benötigst die Quotientenregel immer dann, wenn du einen Bruch von Funktionen ableiten willst. Das heißt, wenn im Zähler (oben) und im Nenner (unten) ein x vorkommt.
Deine Funktion f(x) sieht also so aus:
![Rendered by QuickLaTeX.com \[f(x) = \frac{\textcolor{red}{g(x)}}{\textcolor{blue}{h(x)}} \qquad \underrightarrow{vereinfacht} \qquad f = \frac{\textcolor{red}{g}}{\textcolor{blue}{h}}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-084ad6de6fd730c0b0a4074f613c1e96_l3.png)
Mit dieser Formel kannst du die Ableitung ganz leicht bestimmen:
![Rendered by QuickLaTeX.com \[ f = \frac{\textcolor{red}{g}}{\textcolor{blue}{h}} \quad\Longrightarrow\quad f' = \frac{\textcolor{blue}{h}\cdot \textcolor{orange}{g'} - \textcolor{teal}{h'} \cdot \textcolor{red}{g}}{\textcolor{blue}{h}^2} \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-0a5212a36da347405dd82f561a480bc8_l3.png)
NAZ minus ZAN durch Nenner ins Quadrat
Quotientenregel Ableitung Beispiel
Am besten schaust du dir direkt ein Beispiel dazu an.
Du sollst folgende Funktion mit der Quotienten regel ableiten:
![Rendered by QuickLaTeX.com \[f(x) = \frac{\textcolor{red}{x^2+4x+1}}{\textcolor{blue}{x}}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-3eb65a7ee1c13b3c43fff80ff8f73abe_l3.png)
Dazu gehst du am besten wie folgt vor:
-
Leite den Zähler g und den Nenner h ab. Dazu benötigst du die Potenzregel
.

-
Setze deine Ergebnisse in die Formel ein. Vergiss dabei nicht Klammern um deine Funktionen zu setzen!

-
Vereinfache jetzt deinen Term. Wenn du dich darin noch unsicher fühlst, dann schau dir doch einfach unser extra Video
dazu an.

Die Ableitung von f ist also:
![Rendered by QuickLaTeX.com \[f(x) = \frac{x^2+4x+1}{x} \qquad \underrightarrow{abgeleitet} \qquad f'(x) = \frac{x^2-1}{x^2}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-b8dce8007cd9113593047d0ce6704d59_l3.png)
Wenn du das Beispiel verstanden hast, dann versuch dich doch mal an folgender Aufgabe:
Du sollst diese Funktion mit der Quotientenregel ableiten:
![Rendered by QuickLaTeX.com \[f(x) = \frac{\textcolor{red}{e^x}}{\textcolor{blue}{2x+1}}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-4864ea839ceea51c0186dee0f9970bd7_l3.png)
-
Leite den Zähler g und Nenner h ab.

-
Setze deine Ergebnisse in die Formel ein.

-
Vereinfache.

Die Ableitung von f ist also:
![Rendered by QuickLaTeX.com \[f(x) = \frac{e^x}{2x+1} \qquad \underrightarrow{abgeleitet} \qquad \frac{e^x(2x-1)}{(2x+1)^2}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-a390ff798a9cd52d1b3c60ff3c0d8a19_l3.png)
Weitere Aufgaben findest du noch in unserem Video zum Thema Brüche ableiten .
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Quotientenregel — häufigste Fragen
(ausklappen)
Quotientenregel — häufigste Fragen
(ausklappen)-
Wann kann ich einen Bruch erst vereinfachen statt die Quotientenregel zu nutzen?Du kannst einen Bruch zuerst vereinfachen, wenn sich ein gemeinsamer Faktor in Zähler und Nenner komplett kürzen lässt. Dadurch wird die Funktion einfacher und du brauchst oft keine Quotientenregel mehr. Zum Beispiel wird
 zu
zu  (für
(für  ), dann ist die Ableitung
), dann ist die Ableitung  .
.
-
Wie erkenne ich, ob ich Quotientenregel oder Kettenregel brauche?Du brauchst die Quotientenregel bei einem echten Bruch
 und die Kettenregel bei einer Verschachtelung
und die Kettenregel bei einer Verschachtelung  . Ein Bruch hat klaren Zähler und Nenner, eine Kette hat eine „Funktion in einer Funktion“. Zum Beispiel ist
. Ein Bruch hat klaren Zähler und Nenner, eine Kette hat eine „Funktion in einer Funktion“. Zum Beispiel ist  ein Quotient, aber
ein Quotient, aber  ist eine Kette.
ist eine Kette.
-
Welche Fehler passieren oft beim Minus in der Quotientenregel?Ein häufiger Fehler ist, das Minus in
 zu vergessen oder beim Ausmultiplizieren falsch zu verteilen. Das passiert besonders, wenn
zu vergessen oder beim Ausmultiplizieren falsch zu verteilen. Das passiert besonders, wenn  oder
oder  aus mehreren Termen besteht. Zum Beispiel muss aus
aus mehreren Termen besteht. Zum Beispiel muss aus  wirklich
wirklich  werden.
werden.
-
Wie leite ich einen Bruch ab, wenn im Zähler ein Produkt steht?Du leitest einen Bruch mit Produkt im Zähler ab, indem du im Zähler zuerst die Produktregel für
 anwendest und dann die Quotientenregel nutzt. Setze also
anwendest und dann die Quotientenregel nutzt. Setze also  und berechne
und berechne  . Danach gilt
. Danach gilt  .
.
-
Was muss ich beim Ableiten beachten, wenn der Nenner null werden kann?Wenn der Nenner null werden kann, ist die Funktion an diesen Stellen nicht definiert und dort gibt es auch keine Ableitung. Deshalb müssen diese
 -Werte aus dem Definitionsbereich ausgeschlossen werden, und das gilt auch nach dem Ableiten weiter. Zum Beispiel ist
-Werte aus dem Definitionsbereich ausgeschlossen werden, und das gilt auch nach dem Ableiten weiter. Zum Beispiel ist  nur für
nur für  definiert, ebenso
definiert, ebenso  .
.
Weitere Ableitungsregeln
Die Quotientenregel ist nur eine von vielen Ableitungsregeln. Damit du alle Funktionen richtig ableiten kannst, musst du auch noch andere Regeln beherrschen.
| Ableitungsregel | Funktion | Ableitung |
| Produktregel |  |
 |
| Summenregel |  |
 |
| Differenzregel |  |
 |
| Kettenregel |  |
 |
| Potenzregel |  |
 |
| Faktorregel | 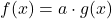 |
 |
Du willst alle Regeln auf einmal erklärt haben? Dann schau doch unser Video dazu an!
