Ableitung Sinus
In diesem Artikel zeigen wir dir, wie du die Ableitung vom Sinus bestimmst und in welchem Zusammenhang sie mit dem Cosinus und der Kettenregel steht. Du möchtest schnell verstehen, wie du jeden Sinus ableiten kannst? Kein Problem. Schau dir einfach unser Video dazu an.
Inhaltsübersicht
Ableitung Sinus einfach erklärt
Die Ableitung vom Sinus kannst du dir leicht merken: Die Sinusfunktion f(x) = sin(x) hat die Ableitung f'(x) = cos(x).
f(x) = sin(x) → f'(x) = cos(x)
Wenn im Sinus aber nicht nur x vorkommt, brauchst du für die Ableitung die Kettenregel . Damit kannst du beispielsweise Funktionen wie f(x) = sin(2x + 5) ableiten.
Sinus Ableitung mit Kettenregel
Die Kettenregel verwendest du immer, wenn im Sinus nicht nur x, sondern eine Funktion steht. Das ist zum Beispiel hier so: f(x) = sin(2x + 5).
Dann gehst du in 3 Schritten vor:
- Schritt 1: Schreibe den Cosinus hin und in den Cosinus die Funktion (innere Funktion):
f'(x) = cos(2x + 5) …
- Schritt 2: Bestimme die Ableitung der Funktion im Sinus:
(2x + 5)‘ = 2
- Schritt 3: Schreibe die Ableitung aus Schritt 2 mit einem Malpunkt hinter den Cosinus:
f'(x) = cos(2x + 5) • 2
Fertig! Den Sinus nennst du dann übrigens äußere Funktion. Schau dir gleich noch ein Beispiel dazu an.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Sinus ableiten — Beispiel
Du willst die Funktion f(x) = sin(3x2 + x) ableiten.
- Schritt 1: Schreibe den Cosinus hin und in den Cosinus die Funktion:
cos(3x2 + x)
- Schritt 2: Bestimme die Ableitung der inneren Funktion. Dafür verwendest du die Potenz- und Faktorregel.
3x2 + x → 6x + 1
- Schritt 3: Setze die Ableitung der ganzen Funktion zusammen:
f'(x) = cos(3x2 + x) • (6x + 1)
Die Sinusfunktion f(x) = sin(x) besitzt in ihrem gesamten Definitionsbereich eine Ableitung, ist also überall differenzierbar . Ihre Ableitungsfunktion ist die Cosinusfunktion f'(x) = cos(x).
Bei vielen Sinusfunktionen brauchst du für die Ableitung die Kettenregel.
Ableitung Sinus Cosinus
Die Ableitung von cos(x) entspricht dem negativen sin(x):
f(x) = cos(x) → f'(x) = -sin(x)
Leitest du nun  erneut ab, erhältst du
erneut ab, erhältst du  . Führst du dieses sin cos Ableiten fort, bekommst du nach insgesamt viermaligem Ableiten wieder die anfängliche Funktion sin(x):
. Führst du dieses sin cos Ableiten fort, bekommst du nach insgesamt viermaligem Ableiten wieder die anfängliche Funktion sin(x):

Wie du siehst, ist die Sinus Cosinus Ableitung nicht besonders schwer. Du musst lediglich aufpassen, dass du die Ableitungen nicht verwechselst.
Ableitung Sinus Beispiele
Nun kann es natürlich auch sein, das du, anders als beim  Ableiten, neben der Kettenregel und der Potenz- und Faktorregel, noch weitere Ableitungsregeln benötigst. In der folgenden Tabelle sind einige solcher Beispiele in Kombination mit Ableitung Sinus.
Ableiten, neben der Kettenregel und der Potenz- und Faktorregel, noch weitere Ableitungsregeln benötigst. In der folgenden Tabelle sind einige solcher Beispiele in Kombination mit Ableitung Sinus.
| Ableitungsregel | Funktion | Ableitung |
| Summenregel | f(x )= g(x) + h(x)
f(x) = sin(3x) + sin(x) |
f'(x) = g'(x) + h'(x)
f'(x) = 3cos(3x) + cos(x) |
| Differenzregel | f(x) = g(x) – h(x)
f(x) = sin(x) – sin(x2) |
f'(x) = g'(x) – h'(x)
f'(x) = cos(x) – cos(x2) • 2x |
| Produktregel | f(x) = g(x) • h(x)
f(x) = sin(-x) • 3x2 |
f'(x) = g'(x) • h(x) + g(x) • h'(x)
f'(x) = -cos(x) • 3x2 + sin(-x) • 6x |
| Quotientenregel |

|
![Rendered by QuickLaTeX.com f'(x)=\frac{g'(x)\cdot h(x)-g(x)\cdot h'(x)}{[h(x)]^2}](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-1128d60300515aa8b8df5c88d4dbbdf9_l3.png)
|
| Faktorregel | f(x) = a • g(x)
f(x) = 4 • sin(x) |
f'(x) = a • g'(x)
f'(x) = 4 • cos(x) |
| Potenzregel | f(x) = xn
f(x) = sin4(x) |
f'(x) = n • xn-1
f'(x) = 4 • sin3(x) • cos(x) |
Weitere Funktionen und Ableitungen
Genauso gut wie die Ableitung von sin x, solltest du dir auch die Ableitungen der folgenden Funktionen einprägen.
| Funktion | Ableitung | |
| Ableitung Cosinus | f(x) = cos(x) | f'(x) = -sin(x) |
| Ableitung Tangens | f(x) = tan(x) |  |
| Wurzel ableiten |  |
 |
| ln ableiten | 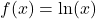 |
 |
| e Funktion ableiten | f(x) = ex | f'(x) = ex |
Ableitung Sinus Herleitung
Anstatt dir die Ableitung der Sinusfunktion zu merken, kannst du sie dir auch herleiten, wenn du sin ableiten möchtest.
Dafür kannst du die h-Methode zur Darstellung der Ableitung nutzen:



Wendest du nun das Additionstheorem
 an, kannst du den Bruch im Zähler folgendermaßen umschreiben:
an, kannst du den Bruch im Zähler folgendermaßen umschreiben:

Jetzt klammerst du  aus und erhältst
aus und erhältst

Als nächstes spaltest du den Bruch in zwei Brüche auf und betrachtest damit zwei separate Grenzwerte.

Da  und
und 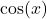 nicht von der Variable
nicht von der Variable  abhängen, kannst du sie jeweils aus dem Grenzwert ziehen:
abhängen, kannst du sie jeweils aus dem Grenzwert ziehen:

Nun hast du beim Erreichen der Grenze  zweimal den unbestimmten Ausdruck
zweimal den unbestimmten Ausdruck  Denn
Denn  und
und 
In so einem Fall kannst du die Regel von l’Hospital anwenden, um die Grenzwerte zu berechnen. Sie sagt aus, dass

und liefert dir damit:


Setzt du nun die berechneten Grenzwerte in die Funktion  ein, bekommst du schließlich als Ergebnis:
ein, bekommst du schließlich als Ergebnis:

Damit hast du dir die Ableitung Sinus hergeleitet.
Ableitung Sinus — häufigste Fragen
(ausklappen)
Ableitung Sinus — häufigste Fragen
(ausklappen)-
Woran erkenne ich schnell, was bei sin(…) die innere Funktion ist?Die innere Funktion ist alles, was in der Klammer von sin(…) steht. Das liegt daran, dass sin als äußere Funktion nur auf diesen gesamten Ausdruck angewendet wird. Zum Beispiel ist bei
 die innere Funktion
die innere Funktion  .
.
-
Welche Fehler passieren am häufigsten bei der Kettenregel mit sin(…)?Am häufigsten wird die Ableitung der inneren Funktion vergessen oder falsch berechnet. Außerdem wird manchmal fälschlich
 statt
statt  hingeschrieben. Beispiel: Bei
hingeschrieben. Beispiel: Bei  ist
ist  , nicht nur
, nicht nur  .
.
-
Wie leite ich sin(x²) ab, ohne aus Versehen sin²(x) zu machen?Du leitest
 mit der Kettenregel ab, nicht mit einer Potenzregel am Sinus. Der Ausdruck
mit der Kettenregel ab, nicht mit einer Potenzregel am Sinus. Der Ausdruck  steht innen, aber sin wird nicht quadriert. Konkret gilt:
steht innen, aber sin wird nicht quadriert. Konkret gilt:  .
.
-
Wie leite ich sin(sin(x)) ab?Du leitest
 mit zweimaliger Kettenregel ab. Zuerst wird die äußere Sinusfunktion zu
mit zweimaliger Kettenregel ab. Zuerst wird die äußere Sinusfunktion zu  , dann kommt die Ableitung der inneren Funktion
, dann kommt die Ableitung der inneren Funktion  dazu. Ergebnis:
dazu. Ergebnis:  .
.
-
Wie leite ich sin(x) ab, wenn x im Bogenmaß oder in Grad angegeben ist?Im Bogenmaß gilt direkt
 , aber bei Grad brauchst du einen Umrechnungsfaktor. Das liegt daran, dass Ableitungsformeln für trigonometrische Funktionen auf Radiant (Bogenmaß) basieren. Für
, aber bei Grad brauchst du einen Umrechnungsfaktor. Das liegt daran, dass Ableitungsformeln für trigonometrische Funktionen auf Radiant (Bogenmaß) basieren. Für  in Grad:
in Grad:  .
.
Ableitung Tangens
Weißt du auch, wie du den Tangens ableitest ? Dafür haben wir ein eigenes Video vorbereitet!


