Video anzeigen

Hochpunkt und Tiefpunkt

Wichtige Inhalte in diesem Video

In diesem Beitrag kannst du dir alles wichtige zum Thema Hochpunkt und Tiefpunkt von Funktionen anschauen. Du lernst eine Schritt-für-Schritt Anleitung, mit welcher du Hochpunkte und Tiefpunkte berechnen kannst. Du möchtest in kurzer Zeit erfahren, wie du einen Hochpunkt und Tiefpunkt bestimmen kannst? Dann schaue dir unser Video zu diesem Thema an.

Inhaltsübersicht

Hochpunkt und Tiefpunkt einfach erklärt

im Videozur Stelle im Video springen

(00:10)

Möchtest du den Hochpunkt und Tiefpunkt einer Funktion f bestimmen, gehst du so vor:

Bilde f’(x): Zuerst leitest du die Funktion ab.
Setze f’(x) = 0: Dann musst du die Nullstellen x_s deiner Ableitung bestimmen. Das sind dann die x-Werte deiner möglichen Hoch- oder Tiefpunkte.
Berechne den y-Wert: Für den y-Wert setzt du die Nullstelle x_s deiner Ableitung in f(x) ein.

Jetzt hast du einen möglichen Hoch- und Tiefpunkt berechnet. Willst du testen, ob es sich um einen Hochpunkt oder Tiefpunkt handelt, brauchst du die zweite Ableitung f’’(x). In die setzt du die Nullstelle x_s der ersten Ableitung ein:

Ist f’’(x_s) < 0, dann handelt es sich um einen Hochpunkt
Ist f’’(x_s) > 0, dann hast du einen Tiefpunkt

Hochpunkt, Tiefpunkt, Hochpunkt berechnen, Tiefpunkt berechnen, Hochpunkt Kurvendiskussion, Tiefpunkt Kurvendiskussion — Hochpunkt und Tiefpunkt

Schau dir jetzt am besten noch ein Beispiel dazu an.

Hochpunkt und Tiefpunkt Beispiel

Schauen wir uns an einem Beispiel an, wie du mit der Ableitung einen Hochpunkt berechnen und einen Tiefpunkt bestimmen kannst. Dazu betrachten wir folgende Funktion

$f(x) = \frac{1}{10}x^3 + 2x^2 - 4x - 12$ .

Bilde f’(x): Zuerst berechnest du die erste Ableitung. Mit Hilfe der Faktor- und Potenzregel erhältst du:
$f'(x) = \frac{3}{10}x^2 + 4x - 4$
Setze f’(x) = 0: Jetzt brauchst du die Nullstellen der ersten Ableitung, damit du mögliche Hochpunkte oder Tiefpunkte bestimmen kannst:
$f'(x) = \frac{3}{10}x^2 + 4x - 4 = 0$

Um die Rechnung zu vereinfachen, multiplizierst du die Gleichung mit 10 und bekommst:

$3x^2 + 40x - 40 = 0$

Diese löst du mit der Mitternachtsformel . Damit ergeben sich die Nullstellen und zu

und .
Berechne den y-Wert: Die Werte setzt du jetzt in deine Funktion f(x) ein:
$f(x_1) = \frac{1}{10}x_1^3 + 2x_1^2 - 4x_1 - 12= \frac{1}{10}(-14,27)^3 + 2\cdot (-14,27)^2 - 4 \cdot (-14,27) - 12 = 161,76$

$f(x_2) = \frac{1}{10}x_2^3 + 2x_2^2 - 4x_2 - 12 = \frac{1}{10}(0,93)^3 + 2\cdot (0,93)^2 - 4 \cdot (0,93) - 12 = -13,91$

Jetzt hast du zwei mögliche Hoch- oder Tiefpunkte berechnet:

$(-14,27 \mid 161,76)$ und $(0,93 \mid -13,91)$

Du willst natürlich noch bestimmen, um welche Art von Punkt es sich handelt. Dafür brauchst du die zweite Ableitung:

$f''(x) = \frac{6}{10}x + 4$

Im letzten Schritt musst du noch x_1 und x_2 in deine zweite Ableitung einsetzen:

$f''(x_1) = \frac{6}{10}x_1 + 4 = \frac{6}{10}(-14,27) + 4 = -4,56 < 0$ ⇒ Hochpunkt
$f''(x_2) = \frac{6}{10}x_2 + 4 = \frac{6}{10}(0,93) + 4 = 4,56 > 0$ ⇒ Tiefpunkt

Der Hochpunkt und Tiefpunkt für die Funktion $f(x) = \frac{1}{10}x^3 + 2x^2 - 4x - 12$ lauten somit

$H(-14,27 \mid 161,76)$ und $T(0,93 \mid -13,91)$ .

Hochpunkt, Tiefpunkt, Beispiel — Funktionsgraph mit Hochpunkt und Tiefpunkt für das Beispiel.

Wichtige Begriffe der Kurvendiskussion

Bevor wir etwas mehr auf die Mathematik hinter dem Hochpunkt und Tiefpunkt eingehen, geben wir dir an dieser Stelle eine kleine Übersicht wichtiger Begriffe der Kurvendiskussion:

In den einzelnen Beiträgen findest du mehr dazu!

Minima und Maxima: lokal vs. global

Nun weißt du, wie du einen Tiefpunkt und Hochpunkt berechnen kannst. Aber vielleicht fragst du dich, wieso die erste Ableitung gleich Null gesetzt wird. Und wieso gibt es Hochpunkte, die aber niedriger als andere Punkte liegen? Wieso nennst du sie dann trotzdem Hoch- oder Tiefpunkte? Das erklären wir dir jetzt! Wir werden uns dabei auf den Fall eines Hochpunkts beschränken. Für einen Tiefpunkt gilt die gleiche Argumentation, wobei du Begriffe wie „am höchsten“ oder „hoch“ durch „am niedrigsten“ oder „tief“ ersetzen musst.

Warum Ableitung Null setzen?

Hochpunkte und Tiefpunkte sind dadurch charakterisiert, dass sich die Funktionswerte an einem Hochpunkt oder Tiefpunkt nicht merklich ändern, wenn du dich nur ein wenig nach links oder nach rechts entlang des Funktionsgraphen bewegst.

Geometrisch bedeutet eine Ableitung von Null, dass die Steigung des Funktionsgraphen an dieser Stelle gleich Null ist. Du kannst also an die Hochpunkte und Tiefpunkte waagerechte Tangenten einzeichnen.

Wieso Bezeichnung „Hoch/Tief“?

Ein Hochpunkt muss nicht zwangsläufig derjenige Punkt sein, der am höchsten liegt. Ein Hochpunkt ist in dem Sinne „hoch“, dass er im Vergleich zu einer kleinen Umgebung um den Hochpunkt höher als alle anderen Punkte in dieser Umgebung liegt. Ist ein solcher Hochpunkt gleichzeitig der höchste Punkt, dann findest du dafür auch die Bezeichnung globaler Hochpunkt oder globales Maximum. Ist das nicht der Fall, so hörst du stattdessen die Bezeichnung lokaler Hochpunkt oder lokales Maximum. Der Zusatz „lokal“ soll dich daran erinnern, dass dieser Hochpunkt nur in einer bestimmten Umgebung „hoch“ ist. Für einen Tiefpunkt findest du die Bezeichnungen globaler Tiefpunkt (globales Minimum) und lokaler Tiefpunkt (lokales Minimum).

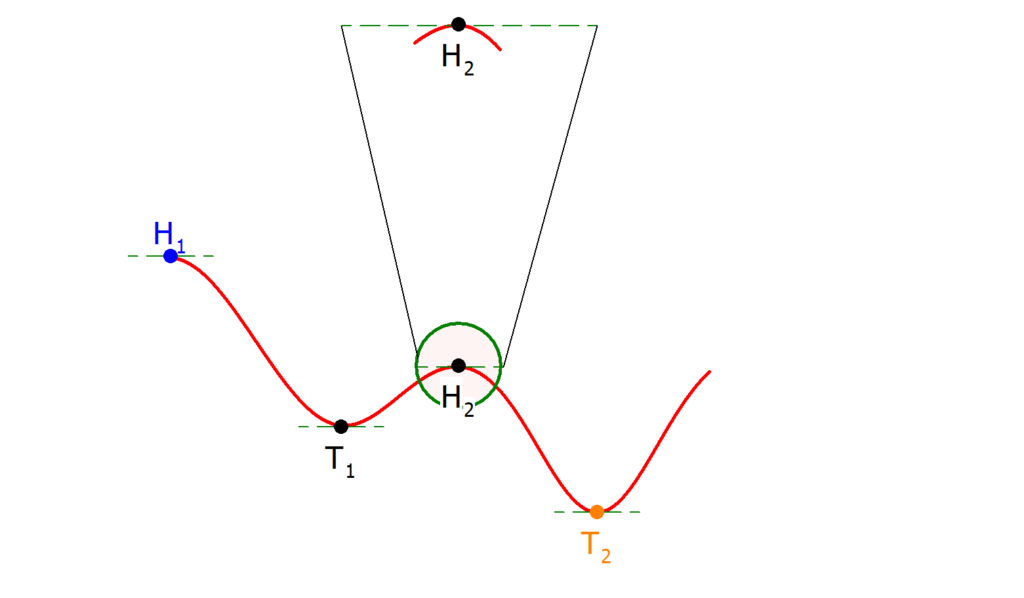
Im folgenden Bild siehst du die Hochpunkte H_1 und H_2 sowie die Tiefpunkte T_1 und T_2 einer Funktion mit eingezeichneten waagerechten Tangenten (grün gestrichelt). Der Hochpunkt H_1 (blau), beziehungsweise der Tiefpunkt T_2 (orange), ist ein globaler Hochpunkt, beziehungsweise ein globaler Tiefpunkt, während H_2 und T_2 (schwarz) ein lokaler Hochpunkt und lokaler Tiefpunkt sind. Zusätzlich wurde in eine Umgebung um den Hochpunkt H_2 gezoomt, um die Bezeichnung „hoch“ zu illustrieren.

Lokal, global, Hochpunkt, Tiefpunkt — Illustration der waagerechten Tangente und Unterschied zwischen global/lokal bei Hochpunkt und Tiefpunkt.

Hochpunkt und Tiefpunkt Aufgaben

In diesem Abschnitt kannst du nochmal in zwei Aufgaben den Tiefpunkt und Hochpunkt berechnen.

Aufgabe 1: Hochpunkt und Tiefpunkt für Polynom zweiten Grades

Gegeben ist die folgende Polynomfunktion

$f(x) = 4x^2 + \frac{3}{2}x - 7$ .

Bestimme den Hochpunkt und Tiefpunkt dieser Polynomfunktion.

Lösung: Aufgabe 1

Schritt 1: Bilde die erste Ableitung:

$f'(x) = 8x + \frac{3}{2}$

Schritt 2: Von der Ableitung werden die Nullstellen bestimmt, das heißt du musst die Gleichung lösen:

$f'(x) = 8x + \frac{3}{2} = 0$

Du erhältst damit die Nullstelle:

$x_s = -\frac{3}{16}$

Schritt 3: Berechne die y-Koordinate:

$f(x_s) = -7,14$

Jetzt hast du einen möglichen Hoch- oder Tiefpunkt berechnet. Du brauchst nur noch die zweite Ableitung:

$f''(x) = 8$

In die setzt du deinen x_s Wert ein und erhältst:

f''(x_s) = 8 > 0 ⇒Tiefpunkt

Damit ergibt sich der Tiefpunkt zu $T \left (-\frac{3}{16} \mid -7,14 \right )$ .

Aufgabe 2: Hochpunkt berechnen und Tiefpunkt bestimmen für Polynom dritten Grades

Gegeben ist die folgende Polynomfunktion

$f(x) = \frac{1}{3}x^3 + \frac{16}{4}x^2 + 7x - 11$ .

Bestimme den Hochpunkt und Tiefpunkt dieser Polynomfunktion.

Lösung: Aufgabe 2

Schritt 1: Du bestimmst die erste Ableitung:

$f'(x) = x^2 + 8x + 7$

Schritt 2: Von der Ableitung werden die Nullstellen bestimmt, das heißt du löst die Gleichung:

$f'(x) = x^2 + 8x + 7=0$

Hierzu verwendest du die pq-Formel und erhältst die Nullstellen

x_1 = -1 und x_2 = -7 .

Schritt 3: Jetzt brauchst du noch die y-Werte. Du setzt x_1 und x_2 in die ursprüngliche Funktion f(x) ein und erhältst die -Koordinaten

y_1 = f(x_1) = -14,33 und y_2 = f(x_2) = 21,67 .

Zu guter Letzt musst du wieder die zweite Ableitung bilden:

$f''(x) = 2x + 8$

Du nimmst die Nullstellen x_1 und x_2 und setzt sie dann in die zweite Ableitung f''(x) ein:

⇒ Tiefpunkt
⇒ Hochpunkt

Damit ergeben sich der Hochpunkt und der Tiefpunkt zu $H (-1 \mid -14,33)$ und $T (-7 \mid 21,67)$ .

Vorzeichenwechselkriterium

Du brauchst gar nicht unbedingt die zweite Ableitung für den Hochpunkt und Tiefpunkt. Es reicht, wenn du die Werte deiner Ableitung in der Nähe deines möglichen Hoch- oder Tiefpunkts anschaust:

Ist f’< 0 links von x_s und f’ > 0 rechts von x_s , dann handelt es sich um einen Tiefpunkt
Ist f’ > 0 links von x_s und f’ < 0 rechts von x_s , dann betrachtest du einen Hochpunkt

Schau dir dazu gleich mal ein Beispiel an:

Bestimme die Hochpunkte und Tiefpunkte von f:

f(x) = x²

Zuerst bildest du wieder die Ableitung:

f’(x) = 2x

Jetzt musst du die Nullstellen deiner Ableitung herausfinden:

f’(x) = 0

2x = 0

x_s = 0

Dein Hoch- oder Tiefpunkt ist also bei x_s gleich 0. Wenn du jetzt einen Wert links von Null einsetzt, z.B. -1, erhältst du eine negative Ableitung:

f’(-1) = -2 < 0

Setzt du einen Wert rechts von Null ein, z.B. 1, erhältst du eine positive Ableitung:

f’(1) = 2 > 0

Also hast du einen Tiefpunkt!

Tiefpunkt und Hochpunkt berechnen

im Videozur Stelle im Video springen

(00:56)

Wie genau kann ich mit Hilfe der ersten und zweiten Ableitung einen Hochpunkt berechnen oder den Tiefpunkt einer Funktion bestimmen? Das beantworten wir dir in diesem Abschnitt in Form einer Schritt-für-Schritt Anleitung.

Die Ausgangssituation ist folgende: Du hast eine Funktion f(x) gegeben und möchtest nun die Hochpunkte berechnen, beziehungsweise die Tiefpunkte bestimmen. Um dieses Ziel zu erreichen, folgst du den folgenden Schritten:

Schritt 1: Erste Ableitung berechnen
Schritt 2: Nullstellen der ersten Ableitung bestimmen
Schritt 3: Zweite Ableitung berechnen
Schritt 4: Nullstellen aus Schritt 2 in die zweite Ableitung einsetzen
Schritt 5: Anhand der Zahl aus Schritt 4 unterscheidest du folgende Fälle (die Nullstellen werden mit abgekürzt):
1. $f''(x_0) = 0 \Longleftrightarrow$ : ist nicht -Koordinate eines Hoch- oder Tiefpunkts.
2. : ist -Koordinate eines Hoch- oder Tiefpunkts. Hier unterscheidest du dann noch die Fälle
  1. $f''(x_0) > 0 \Longleftrightarrow$ ist -Koordinate eines Tiefpunkts.
  2. $f''(x_0) < 0 \Longleftrightarrow$ ist -Koordinate eines Hochpunkts.
Schritt 6: Hat sich im fünften Schritt ergeben, dass die -Koordinate für einen Hochpunkt oder Tiefpunkt ist, so setzt du in die ursprüngliche Funktion ein, um die -Koordinate des Hoch- oder Tiefpunkts zu bestimmen, also .

Wendepunkt berechnen

Super! Hoch- und Tiefpunkte kannst du jetzt problemlos berechnen. Ein weiteres Thema zur Kurvendiskussion, das du unbedingt können musst, ist die Berechnung von Wendepunkten. Wendepunkte sind die Punkte, an denen ein Funktionsgraph von einer Rechtskrümmung in die Linkskrümmung wechselt oder umgekehrt. Damit du deine nächste Prüfung gut meisterst, solltest du unbedingt wissen, wie du sie berechnest. Schau dir am besten direkt unser Video dazu an!