Ableitungsregeln
In diesem Beitrag zeigen wir dir anhand vieler Beispiele, welche Ableitungsregeln es gibt und wie du die Ableitungsregeln richtig anwendest.
Du möchtest die Ableitungsregeln in kurzer Zeit erlernen? Dann schaue dir unser Video dazu an.
Möchtest du jedoch verstehen, was eine Ableitung eigentlich ist oder wie du bestimmte Funktionen ableitest ? Dann klicke einfach auf den Link!
Inhaltsübersicht
Ableitungsregeln einfach erklärt
Die Ableitungsregeln sind eine Art „Bauanleitung“, wie du zusammengesetzte Funktionen ableiten kannst. Bildlich kannst du dir einen LEGO-Baukasten vorstellen, indem du viele einfache Funktionen hast, die du schon einmal abgeleitet hast. Mit den Ableitungsregeln kannst du dann auch komplizierte Funktionen ableiten, die aus kleineren LEGO-Bausteinen bestehen.
Ableitungen von einfachen Funktionen wie  oder
oder 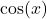 kennst du vielleicht bereits. Diese Funktionen sind keine komplizierten Ausdrücke. Insbesondere steht im Argument der Funktion immer nur
kennst du vielleicht bereits. Diese Funktionen sind keine komplizierten Ausdrücke. Insbesondere steht im Argument der Funktion immer nur  alleine, ohne Faktoren oder Potenzen. Wie sieht aber die Situation aus, wenn ein Ausdruck wie
alleine, ohne Faktoren oder Potenzen. Wie sieht aber die Situation aus, wenn ein Ausdruck wie  abzuleiten ist? Du kannst dir diesen Ausdruck aus den beiden Bausteinen
abzuleiten ist? Du kannst dir diesen Ausdruck aus den beiden Bausteinen 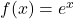 und
und  zusammengebaut vorstellen. Für diese beiden Bausteine kennen wir die Ableitungen, benötigen jedoch die Ableitungsregeln.
zusammengebaut vorstellen. Für diese beiden Bausteine kennen wir die Ableitungen, benötigen jedoch die Ableitungsregeln.
Ableitungsregeln Übersicht
| Ableitungsregel | Funktion | Ableitung |
| Summenregel |  |
 |
| Differenzregel |  |
 |
| Produktregel |  |
 |
| Quotientenregel |  |
![Rendered by QuickLaTeX.com f'(x)=\frac{g'(x)\cdot h(x)-g(x)\cdot h'(x)}{[h(x)]^2}](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-1128d60300515aa8b8df5c88d4dbbdf9_l3.png) |
| Kettenregel |  |
 |
| Potenzregel |  |
 |
| Faktorregel | 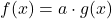 |
 |
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Faktorregel und Potenzregel
Die ersten Ableitungsregeln, die wir uns anschauen, sind die Faktorregel und die Potenzregel.
Kennst du die Ableitung einer Funktion  , dann gilt nach der Faktorregel für die Ableitung der Funktion
, dann gilt nach der Faktorregel für die Ableitung der Funktion 
 .
.
Für Potenzfunktionen

gilt nach der Potenzregel
 .
.
In Worten gefasst, bedeutet die Faktorregel, dass du dir bei einem Produkt aus Zahl und Funktion die Zahl wegdenken kannst, wenn du die Ableitung ausrechnen möchtest. Danach schreibst du die Zahl wieder hin. Die Potenzregel hingegen sagt dir folgendes: “ Schreibe den Exponenten vor das x und reduziere dann den Exponenten um eins“.
Beispiel
Schauen wir uns ein kurzes Beispiel für jede dieser beiden Ableitungsregeln an. Möchten wir die Funktion

ableiten, dann können wir die Faktorregel verwenden. Wir erhalten
 .
.
Interessieren wir uns dagegen dafür, die Funktion

abzuleiten, dann bekommen wir nach der Potenzregel
 .
.
Möchtest du noch mehr Beispiele zur Potenzregel und Faktorregel sehen, dann schau dir unseren extra Beitrag dazu an.
Summenregel und Differenzenregel
Die nächsten beiden Ableitungsregeln sind die Summenregel und die Differenzenregel .
Kennst du die Ableitungen der Funktionen  und
und  , dann gilt nach der Summenregel für die Summe
, dann gilt nach der Summenregel für die Summe 
 .
.
Die Summenregel sagt dir, wie du die Summe zweier Funktionen ableitest. Dabei berechnest du die Ableitungen der einzelnen Funktionen separat und addierst sie anschließend.
Wie funktioniert das aber für Differenzen? Betrachte hierzu folgende allgemeine Funktion
 .
.
Hierbei kannst du analog zur Summenregel vorgehen und statt dem Plus ein Minus schreiben
 .
.
Beispiel
Nehmen wir an, dass wir die Funktion

ableiten möchten. Dann berechnest du die Ableitung von  und von
und von  separat. Du erhältst
separat. Du erhältst
 und
und

Nach der Summenregel musst du diese Ergebnisse nur noch addieren, um die Ableitung von  zu erhalten
zu erhalten
 .
.
Produktregel
Betrachten wir nun die Produktregel . Sie hilft uns Funktionen abzuleiten, die als Produkt von mehreren Funktionen zusammengebaut sind.
Kennst du die Ableitungen der Funktionen  und
und  , dann gilt für das Produkt
, dann gilt für das Produkt 
 .
.
Beachte, dass die Produktregel nicht lautet
 .
.
Du kannst also nicht wie bei der Summenregel bloß die einzelnen Ableitungen ausrechnen und diese dann miteinander multiplizieren. Du musst zwar weiterhin die einzelnen Ableitungen berechnen, die Produktregel instruiert dich aber dazu, diese auf eine ganz bestimmte Art und Weise zu verknüpfen. Die Ableitung eines Produkts ist eine Summe, deren Summanden wieder Produkte sind. In Worten kannst du dir diese Ableitungsregel folgendermaßen merken
„erste Funktion abgeleitet MAL zweite Funktion nicht abgeleitet PLUS erste Funktion nicht abgeleitet MAL zweite Funktion abgeleitet“.
Beispiel
Ein Beispiel hierfür wäre die Funktion

Zunächst bestimmst du die Ableitungen der zwei Funktionen f und g


Anschließend setzt du sie in die Formel der Produktregel ein und erhältst damit

 .
.
Quotientenregel
Als nächsten Baustein schauen wir uns die Quotientenregel an. Wie der Name bereits andeutet, ist die Quotientenregel eine Bauanleitung dafür, wie du Funktionen ableitest, die als Quotient anderer Funktionen zusammengebaut sind.
Kennst du die Ableitungen der Funktionen  und
und  , dann gilt für den Quotienten
, dann gilt für den Quotienten 
 .
.
Bei einem Quotienten kannst du also die Ableitung nicht bloß durch Division der einzelnen Ableitungen berechnen. Vielleicht fällt dir die Ähnlichkeit des Zählers mit der Produktregel auf. Der Unterschied besteht nur im Minuszeichen. Beachte weiterhin, dass du die Quotientenregel nur für  -Werte verwenden kannst, bei welchen die Funktion
-Werte verwenden kannst, bei welchen die Funktion  nicht gleich Null wird. Ansonsten würdest du beim Ableiten durch Null dividieren, was mathematisch nicht erlaubt ist!
nicht gleich Null wird. Ansonsten würdest du beim Ableiten durch Null dividieren, was mathematisch nicht erlaubt ist!
Beispiel
Sieh dir zum Beispiel die Funktion

an. Um die Quotientenregel anwenden zu können, leitest du zunächst Zähler und Nenner einzeln ab:


Jetzt setzt du diese in die obige Formel ein:


Das Ergebnis ist die Ableitung 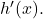
Kettenregel
Bisher haben wir uns nur Ableitungsregeln angesehen, die uns sagen, wie wir Funktionen ableiten, die wir aus anderen Funktionen unter Verwendung der vier Grundrechenarten zusammengebaut haben. Nun können Funktionen auch durch den Prozess der „Verkettung “ zu einer neuen Funktion kombiniert werden. Hierfür benötigst du die
Kennst du die Ableitungen der Funktionen  und
und  , dann gilt für die Verkettung
, dann gilt für die Verkettung 
 .
.
Die Funktion  findest du auch unter der Bezeichnung innere Funktion. Dagegen heißt
findest du auch unter der Bezeichnung innere Funktion. Dagegen heißt  äußere Funktion. Bei der Kettenregel musst du also die Ableitung der äußeren Funktion (auch äußere Ableitung genannt) mit der Ableitung der inneren Funktion (auch innere Ableitung genannt) multiplizieren.
äußere Funktion. Bei der Kettenregel musst du also die Ableitung der äußeren Funktion (auch äußere Ableitung genannt) mit der Ableitung der inneren Funktion (auch innere Ableitung genannt) multiplizieren.
„Äußere Ableitung mal innere Ableitung.“
Beispiel
Ein Beispiel für eine verkettete Funktion wäre
 .
.
In diesem Fall lautet die
- innere Funktion f(x) und ihre Ableitung f'(x):

- äußere Funktion g(x) und ihre Ableitung g'(x):

Für  setzt du nun die Ableitungen
setzt du nun die Ableitungen  und
und  zusammen mit
zusammen mit  in die Formel der Kettenregel ein:
in die Formel der Kettenregel ein:


Noch mehr Beispiele findest du in unserem extra Beitrag .
Ableitung wichtiger Funktionen
Bevor wir uns der Anwendung der Ableitungsregeln auf komplizierte Funktionen widmen, fassen wir kurz nochmal die Ableitungen wichtiger Funktionen zusammen. Diese Zusammenfassung ist in folgender Tabelle wiedergegeben.
| Funktion | Ableitung | |
| Wurzel ableiten |  |
 |
| Ableitung Cosinus |  |
 |
| Ableitung Sinus |  |
 |
| Ableitung Tangens |  |
 |
| e Funktion ableiten |  |
 |
| ln ableiten | 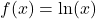 |
 |
Ableitungsregeln Anwenden
In diesem Abschnitt schauen wir uns eine komplizierte Funktion an, die wir ableiten möchten. Dieses Anwendungsbeispiel dient als Muster für die Aufgaben zu den Ableitungsregeln, die du am Ende des Artikels findest.
Beispiel: Ableitungsregeln anwenden
Wir möchten die Funktion

ableiten. Wir erkennen, dass die Funktion ein Produkt aus zwei Funktionen ist
 und
und

Im ersten Schritt verwenden wir die Produktregel
 .
.
Wir benötigen also die Komponenten  und
und  . Schauen wir uns zunächst
. Schauen wir uns zunächst  an. Die Funktion
an. Die Funktion  ist eine Verkettung aus der inneren Funktion
ist eine Verkettung aus der inneren Funktion  und der äußeren Funktion
und der äußeren Funktion  .
.
Nach der Kettenregel gilt also
 .
.
Für die Funktion  können wir die Potenzregel anwenden. Wir erhalten
können wir die Potenzregel anwenden. Wir erhalten
 .
.
Der Faktor 1 kommt durch das Ableiten der Funktion 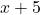 . Wir haben nun alle Komponenten beisammen und erhalten
. Wir haben nun alle Komponenten beisammen und erhalten
 .
.
Das Endergebnis mag zwar erschreckend aussehen, aber beachte, dass wir hier nur systematisch die Ableitungsregeln verwendet haben. Du identifizierst als erstes, was für eine „Form“ von Funktion dir vorliegt (Summe, Produkt, Quotient, Verkettung) und dann unterteilst du diese Form in ihre einzelnen Bestandteile. Danach untersuchst du die einzelnen Bestandteile genauer und versuchst ihre „Form“ zu erkennen. Wenn du dann alle Bestandteile zusammen hast, baust du die gesuchte Ableitung gemäß den „Bauanleitungen“ (also den Ableitungsregeln) zusammen.
Ableitungsregeln Aufgaben
In diesem Abschnitt zeigen wir dir zwei Aufgaben zu den Ableitungsregeln. Die erste Aufgabe beinhaltet ein Produkt von Funktionen, während die zweite einen Quotienten von Funktionen behandelt.
Ableitungsregeln Aufgabe 1: Produkt von Funktionen
Die folgende Funktion soll abgeleitet werden
 .
.
(a) Welche „Form“ von Funktion hast du vorliegen und welche Ableitungsregel musst du verwenden? Notiere die Ableitungsregel.
(b) Identifiziere die einzelnen Bestandteile der festgelegten „Form“.
(c) Nutze die Ableitungsregeln, um die einzelnen Bestandteile abzuleiten.
(d) Baue die gesuchte Ableitung zusammen durch Anwendung der Ableitungsregeln.
Lösung Aufgabe 1
(a) Die Funktion ist als Produkt zweier Funktionen zusammengebaut. Daher muss die Produktregel verwendet werden. Diese lautet
 .
.
(b) Die Funktion  ist das Produkt der Funktionen
ist das Produkt der Funktionen
 und
und
 .
.
(c) Die Funktion  ist die Verkettung der Funktionen
ist die Verkettung der Funktionen  und
und  .
.
Gemäß der Kettenregel erhalten wir
 .
.
Die Funktion  ist die Verkettung der Funktionen
ist die Verkettung der Funktionen 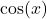 und
und  .
.
Erneut erhalten wir nach der Kettenregel
 .
.
(d) Wir haben nun alle Bestandteile zusammen. Unter Verwendung der Produktregel bekommen wir

Ableitungsregeln Aufgabe 2: Quotient von Funktionen
Die folgende Funktion soll abgeleitet werden
 .
.
(a) Welche „Form“ von Funktion hast du vorliegen und welche Ableitungsregel musst du verwenden? Notiere die Ableitungsregel.
(b) Identifiziere die einzelnen Bestandteile der festgelegten „Form“.
(c) Nutze die Ableitungsregeln, um die einzelnen Bestandteile abzuleiten.
(d) Baue die gesuchte Ableitung zusammen durch Anwendung der Ableitungsregeln.
Ableitungsregeln — häufigste Fragen
(ausklappen)
Ableitungsregeln — häufigste Fragen
(ausklappen)-
Was sind Ableitungsregeln in einfachen Worten?Ableitungsregeln sind Bauanleitungen, mit denen sich zusammengesetzte Funktionen systematisch ableiten lassen. Der Grundgedanke ist: Eine komplizierte Funktion besteht aus einfacheren „Bausteinen“, deren Ableitungen bekannt sind, und die Regeln sagen, wie man diese Ableitungen korrekt kombiniert. So wird aus
 eine Verkettung aus
eine Verkettung aus  und
und  .
.
-
Wie erkenne ich, ob ich die Summenregel anwenden muss?Die Summenregel brauchst du, wenn die Funktion als Summe zweier Teilfunktionen aufgebaut ist, also die Form
 hat. Dann leitest du beide Teile getrennt ab und addierst die Ergebnisse. Zum Beispiel wird aus
hat. Dann leitest du beide Teile getrennt ab und addierst die Ergebnisse. Zum Beispiel wird aus  die Ableitung
die Ableitung  .
.
-
Wie merke ich mir die Produktregel richtig?Die Produktregel merkst du dir als Satz: „erste Funktion abgeleitet mal zweite nicht abgeleitet plus erste nicht abgeleitet mal zweite abgeleitet“. Das ist wichtig, weil die Ableitung eines Produkts nicht
 ist. Formal gilt
ist. Formal gilt  .
.
-
Wann brauche ich die Quotientenregel statt der Produktregel?Die Quotientenregel brauchst du, wenn die Funktion ein Bruch aus zwei Funktionen ist, also
 . Dann wird nicht „oben und unten getrennt abgeleitet“, sondern es gilt
. Dann wird nicht „oben und unten getrennt abgeleitet“, sondern es gilt  . Außerdem darf
. Außerdem darf  nicht Null sein.
nicht Null sein.
-
Wie finde ich bei der Kettenregel die innere Funktion?Die innere Funktion ist bei der Kettenregel der Ausdruck, der „innen“ in einer anderen Funktion steht, also in
 das
das  . Die äußere Funktion ist die Hülle darum. Zum Beispiel ist bei
. Die äußere Funktion ist die Hülle darum. Zum Beispiel ist bei  die innere Funktion
die innere Funktion  und die äußere Funktion
und die äußere Funktion  .
.
Lösung Aufgabe 2
(a) Die Funktion ist als Quotient zweier Funktionen zusammengebaut. Daher muss die Quotientenregel verwendet werden. Diese lautet
 .
.
(b) Die Funktion  ist der Quotient aus den Funktionen
ist der Quotient aus den Funktionen
 und
und
 .
.
(c) Die Funktion  ist die Verkettung aus den Funktionen
ist die Verkettung aus den Funktionen
 und
und
 .
.
Nach der Kettenregel erhalten wir
 .
.
Die Funktion  ist die Summe aus den Funktionen
ist die Summe aus den Funktionen
 und
und
 .
.
Der letzte Summand kann unter Verwendung der Faktorregel abgeleitet werden. Wir erhalten insgesamt
 .
.
(d) Wir haben nun alle Bestandteile zusammen. Unter Verwendung der Quotientenregel bekommen wir
 .
.




