Video

Quiz

Hier geht's zum Video „Quadratische Funktionen“

Hier geht's zum Video „Nullstellen berechnen“

Hier geht's zum Video „Quadratische Gleichungen“

Mitternachtsformel

Wichtige Inhalte in diesem Video

Mitternachtsformel einfach erklärt

Diskriminante der quadratischen Lösungsformel

Quadratische Gleichungen mittels Mitternachtsformel berechnen

In diesem Artikel erklären wir dir, wie du mithilfe der Mitternachtsformel quadratische Gleichungen lösen kannst oder die Nullstellen einer Parabel berechnest. Das erklären wir dir an mehreren Beispielen.

Du möchtest die Mitternachtsformel und ihre Anwendung schnell verstehen? Dann schau unser Video dazu an!

Inhaltsübersicht

Mitternachtsformel einfach erklärt

im Videozur Stelle im Video springen

Die Mitternachtsformel ist eine der wichtigsten Formeln in der Mathematik, um quadratische Gleichungen zu lösen. Also zum Beispiel

x²+2x+1=0
2x²-5x=x²+x-9
-x²+4x=10

Die allgemeine Form einer quadratischen Gleichung ist somit

ax²+bx+c=0,

mit Parametern a, b, c und $a\neq 0$ . Willst du ihre beiden Lösungen x₁ und x₂ bestimmen, so verwendest du dazu die Mitternachtsformel:

Mitternachtsformel

$x_{1,2} = \cfrac{-b \pm \sqrt{b^2-4ac}}{2a}$

Das bedeutet, du erhältst durch Einsetzen von a, b und c im Allgemeinen zwei Lösungen

$x_1 = \cfrac{-b + \sqrt{b^2-4ac}}{2a}$

$x_2 = \cfrac{-b - \sqrt{b^2-4ac}}{2a}$ .

Übrigens: Die Mitternachtsformel hat ihren Namen daher, weil sie so wichtig ist, dass du sie selbst nachts um 12 Uhr auswendig aufsagen können solltest!

Diskriminante der quadratischen Lösungsformel

im Videozur Stelle im Video springen

Hinweis: Wenn dir der folgende Abschnitt zu schnell geht, schau dir zuerst unser eigenes Einsteiger-Video zur Mitternachtsformel an.

Der Term b²-4ac unter der Wurzel der Mitternachtsformel wird Diskriminante genannt. Dabei wird niemand diskriminiert, das Wort kommt lediglich aus dem Lateinischen und bedeutet „unterscheiden“. Die Diskriminante gibt dir Auskunft darüber, ob eine quadratische Gleichung eine, zwei oder keine Lösung hat. Das erkennst du ganz einfach an ihrem Vorzeichen

Diskriminante

D=b²-4ac
D> 0: Die quadratische Gleichung hat zwei Lösungen
D= 0: Die quadratische Gleichung hat eine Lösung
D< 0: Die quadratische Gleichung hat keine Lösung

Interpretierst du ax²+bx+c als quadratische Funktion , dann kannst du an dem Vorzeichen der Diskriminante die Anzahl der Nullstellen der Parabel ablesen.

Nullstellen Parabeln, Nullstelle, quadratische Funktionen, Diskriminante — Anzahl der Nullstellen einer quadratischen Funktion

Quadratische Gleichungen mittels Mitternachtsformel berechnen

im Videozur Stelle im Video springen

Willst du die Mitternachtsformel zur Berechnung quadratischer Funktionen anwenden, dann befolgst du am besten die folgende Schritt-für-Schritt-Anleitung. Hierfür verwenden wir als konkretes Beispiel die quadratische Gleichung

$\frac{1}{2}x^2+30 = 8x$ .

Schritt 1: Forme die Gleichung so um, dass auf eine der beiden Seiten die Null steht. Damit bringst du die quadratische Gleichung auf die allgemeine Form.

$\begin{align*} \frac{1}{2}x^2+30 &= 8x \quad | -8x \\ \frac{1}{2}x^2-8x+30 &= 0 \end{align*}$

Schritt 2: Lies als nächstes die Koeffizienten a, b und c ab.

$a= \frac{1}{2}$ , b = -8, c = 30

Schritt 3: Setze a, b und c in die Mitternachtsformel ein:

$x_{1,2} = \cfrac{-b \pm \sqrt{b^2-4ac}}{2a}$

$x_{1,2} = \cfrac{-(-8) \pm \sqrt{(-8)^2-4\cdot \frac{1}{2}\cdot 30}}{2 \cdot \frac{1}{2}}$

Schritt 4: Berechne die Ergebnisse

$x_{1,2} = \cfrac{8 \pm \sqrt{64-2 \cdot 30}}{1} = 8 \pm \sqrt{64-60} = 8 \pm \sqrt{4} =8 \pm 2$

$\Longrightarrow \quad \quad x_1 =8+2= 10$ und x_2 = 8-2=6

Schritt 5: Schreibe die Lösungsmenge auf

$\mathbb{L} = \{6; 10\}$

Dieses Vorgehen kann manchmal abgekürzt werden, wenn bestimmte Sonderfälle vorliegen. Dann kann es auch sein, dass du die Nullstellen schneller ohne Mitternachtsformel berechnest. Das ist beispielsweise dann der Fall, wenn b oder c gleich Null sind.

Sonderfall b=0

im Videozur Stelle im Video springen

Ist in der quadratischen Gleichung b=0, so kannst du das Ergebnis zwar mithilfe der Mitternachtsformel berechnen, jedoch bist du vermutlich schneller, wenn du einfach die Wurzel ziehst. Der Term hat dann immer die Form

ax²+c=0.

Du kannst ihn umformen, indem du nach x² auflöst und dann die Wurzel ziehst:

$x^2 = \frac{-c}{a}$

$x_{1,2} = \pm \sqrt{\frac{-c}{a}}$

Willst du beispielsweise 4x^2-36=0 berechnen, so erhältst du als Ergebnis

$4x^2=36 \quad \quad \quad \quad \quad \bigg| \div 4$

x^2 = 9

$x_{1,2} = \pm \sqrt{9} = \pm 3$

Sonderfall c=0

im Videozur Stelle im Video springen

Hast du dahingegen einen Term gegeben, bei dem c=0 ist, so löst du die Funktionsgleichung am besten durch Ausklammern. Dann kannst du die Nullstellen der beiden Faktoren separat bestimmen,

ax²+bx=0

x(ax+b)=0

x_1 = 0 und

$ax+b=0 \Longleftrightarrow ax = -b \quad \Longrightarrow \quad x_2 = -\frac{b}{a}$

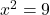
Mitternachtsformel Übungen

Wie du konkret vorgehst, zeigen wir dir nun an einigen Beispielen, damit du auch die Fälle siehst, bei denen es nur eine oder gar keine Lösung gibt.

Beispiel 1: Mitternachtsformel mit zwei Lösungen

Gesucht ist die Lösungsmenge der quadratischen Gleichung

2x^2-6x = 8 .

Im ersten Schritt stellen wir die Gleichung um, sodass die rechte Seite Null ergibt. Stellen also die allgemeine Form der quadratischen Gleichung auf

2x^2-6x-8=0 .

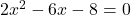Als nächstes bestimmen wir die Parameter a=2, b=-6 und c=-8, die wir in die Mitternachtsformel einsetzen.

$x_{1,2} = \cfrac{-(-6)\pm \sqrt{(-6)^2-4\cdot 2 \cdot (-8)}}{2\cdot 2}$

$= \cfrac{6 \pm \sqrt{36+64}}{4}$

$= \cfrac{6 \pm \sqrt{100}}{4}$

$= \cfrac{6 \pm 10}{4}$

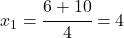$x_1 = \cfrac{6+10}{4}=4$ und $x_2 =\cfrac{6-10}{4}=-1$

Nun müssen wir nur noch die Lösungsmenge $\mathbb{L}=\{-1 ; 4\}$ aufschreiben. Es gibt also zwei Lösungen.

Beispiel 2: Mitternachtsformel mit einer Lösung

Im obigen Beispiel hast du zwei Lösungen erhalten, da die Diskriminante größer als Null war. Für Fälle mit D=0, gibt es jeweils nur eine Nullstelle, wie du am folgenden Beispiel siehst.

x^2-6x+9 =0

Da dieser Term schon in allgemeiner Form vorliegt, überspringen wir Schritt 1 und machen direkt mit Schritt 2 der Anleitung weiter, indem wir a=1, b=-6 und c=9 bestimmen. Einsetzen in die Mitternachtsformel ergibt

$x_{1,2} = \cfrac{-(-6)\pm \sqrt{(-6)^2-4\cdot 1 \cdot 9}}{2\cdot 1}$

$= \cfrac{6\pm \sqrt{36-36}}{2} = \cfrac{6\pm 0}{2}=3$

Dieses Ergebnis kannst du so interpretieren, dass der Scheitel der quadratischen Funktion f(x)=x^2-6x+9 ihre einzige Nullstelle ist. Es gibt also nur eine Lösung $\mathbb{L}=\{3\}$ .

Beispiel 3: Mitternachtsformel mit keiner Lösung

Für quadratische Funktionen ohne Nullstellen ist die Diskriminante D<0, was bedeutet, dass du einen negativen Ausdruck unter der Wurzel erhältst. Die Lösungsmenge ist hier die leere Menge $\mathbb{L} = \emptyset = \{\}$ . Das siehst du auch direkt am Beispiel

$\frac{1}{2}x^2+2x+5=0$ .

Setzen wir $a=\frac{1}{2}$ , b=2 und c=5 in die Mitternachtsformel ein, so erhalten wir

$x_{1,2} = \cfrac{-2\pm \sqrt{2^2-4\cdot \frac{1}{2} \cdot 5}}{2\cdot \frac{1}{2}}$

$= \cfrac{-2\pm \sqrt{4-10}}{1}$

$= -2 \pm \sqrt{-6}$

Da die Wurzelfunktion nicht für negative Zahlen definiert ist, hat diese Gleichung kein Ergebnis!

Mitternachtsformel Herleitung

Vielleicht fragst du dich, woher die Mitternachtsformel eigentlich kommt. Für ihre Herleitung löst man lediglich die allgemeine quadratische Gleichung nach x auf.

$\begin{align*} ax^2+bx+c&=0 \enspace &|& -c \\ ax^2+bx&=-c \enspace &|& : a \\ x^2+\cfrac{b}{a}x &= -\cfrac{c}{a} \end{align*}$

Um an dieser Stelle weiterrechnen zu können, benötigen wir die quadratische Ergänzung der linken Seite. Dazu addieren wir auf beiden Seiten $\left( \frac{1}{2}\cdot \frac{b}{a}\right)^2= \left(\frac{b}{2a}\right)^2$

$x^2+\frac{b}{a}x +\left(\frac{b}{2a}\right)^2= -\frac{c}{a} + \left(\frac{b}{2a}\right)^2$

$x^2+\frac{b}{a}x +\left(\frac{b}{2a}\right)^2= -\frac{c}{a} + \frac{b^2}{4a^2}$

Die rechte Seite fassen wir noch weiter zusammen, indem wir $-\frac{c}{a}$ mit erweitern und die Terme dann auf einen Bruchstrich schreiben.

$x^2+\cfrac{b}{a}x +\left(\cfrac{b}{2a}\right)^2= \cfrac{b^2-4ac}{4a^2}$

Auf der linken Seite hält sich eine binomische Formel versteckt, sodass wir diesen Term auch umformen können als

$\left(x+\cfrac{b}{2a}\right)^2= \cfrac{b^2-4ac}{4a^2}$ .

Davon ziehen wir nun die Wurzel und erhalten

$x+\cfrac{b}{2a} =\pm \sqrt{\cfrac{b^2-4ac}{4a^2}}$

Vereinfachen und Subtraktion von $\frac{b}{2a}$ ergibt schon fast die Mitternachtsformel

$x = -\cfrac{b}{2a}\pm \sqrt{\cfrac{b^2-4ac}{4a^2}}$

$x = -\cfrac{b}{2a}\pm \cfrac{\sqrt{b^2-4ac}}{2a}$

$\Rightarrow x_{1,2} = \cfrac{-b\pm \sqrt{b^2-4ac}}{2a}$

Merke: Dass wir stattdessen x_1 und x_2 und $\pm$ schreiben, sorgt dafür, dass du die zweite Lösung nicht vergisst!

pq Formel

Wenn du eine quadratische Gleichung in Normalform gegeben hast, bei der a=1 ist, kannst du statt der Mitternachtsformel auch die pq Formel verwenden. Hier schreibst du statt b ein p und q entspricht unserem c.

Für Terme der Form x^2+px+q=0 kannst du somit auch die pq Formel verwenden:

$x^2+p\cdot x +q = 0 \quad \Longleftrightarrow \quad x_{1,2} = -\cfrac{p}{2}\pm \sqrt{\left(\cfrac{p}{2}\right)^2-q}$

Merke: Wenn du eine allgemeine quadratische Funktion ax²+bx+c=0 gegeben hast, kannst du auch durch a dividieren um die pq Formel anzuwenden. In diesem Fall ist $p=\frac{b}{a}$ und $q=\frac{c}{a}$ .

$\begin{align*} ax^2&+bx ~ +c \quad | : a \\ x^2&+\frac{b}{a}x+\frac{c}{a} \end{align*}$

Ausführlich und mit vielen Beispielen erklären wir dir das in einem eigenen Video. Du willst quadratische Gleichungen immer ohne Probleme lösen können? Dann musst du auf jeden Fall unser Video zur pq-Formel anschauen.

pq formel, pq-formel, Nullstellen berechnen, quadratische gleichungen lösen, diskriminante — Zum Video: pq Formel

zur Videoseite: Mitternachtsformel

Beliebte Inhalte aus dem Bereich Algebra

Quadratische Gleichungen lösen

Mitternachtsformel einfach erklärt

Mitternachtsformel

pq Formel einfach erklärt

Hallo, leider nutzt du einen AdBlocker.

Auf Studyflix bieten wir dir kostenlos hochwertige Bildung an. Dies können wir nur durch die Unterstützung unserer Werbepartner tun.

Schalte bitte deinen Adblocker für Studyflix aus oder füge uns zu deinen Ausnahmen hinzu. Das tut dir nicht weh und hilft uns weiter.

Danke!
Dein Studyflix-Team

Wenn du nicht weißt, wie du deinen Adblocker deaktivierst oder Studyflix zu den Ausnahmen hinzufügst, findest du hier eine kurze Anleitung. Bitte .