Lambert Beersches Gesetz
Lässt man elektromagnetische Strahlung durch eine absorbierende Substanz strahlen, so kann man unter Verwendung des Lambert Beerschen Gesetzes die Substanzkonzentration bestimmen. In diesem Beitrag erfährst du, was das Gesetz besagt und wie du es herleiten kannst. Außerdem betrachten wir, in welchen Bereichen es das Gesetz Anwendung und wann es überhaupt Gültigkeit besitzt.
Möchtest du die Informationen kurz und verständlich mit Bild und Ton erklärt bekommen, dann schau unser Video dazu an!
Inhaltsübersicht
Lambert Beersches Gesetz einfach erklärt
Das Lambert Beersche Gesetz ist ein Spezialfall der Strahlungstransportgleichung und findet häufig Anwendung in der Photometrie . Es ist auch unter dem Namen Bouguer Lambert Beersches Gesetz bekannt.
Lambert Beersches Gesetz Geschichte
Im Jahr 1729 entdeckte Pierre Bouguer, dass die Strahlungsintensität einer elektromagnetischen Strahlung beim Durchqueren eines absorbierenden Materials mit der Weglänge abnimmt. Da nach Übermittlungen auch J. H. Lambert an der Entwicklung des Gesetzes beteiligt gewesen sein soll, wird es heute Bouguer Lambertsches Gesetz genannt. Im Jahre 1852 modifizierte A. Beer das Bouguer Lambertsche Gesetz, sodass diese modifizierte Form nun unter dem Namen Lambert Beersches Gesetz bekannt ist.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Lambert Beersches Gesetz Formel
Das Lambert Beersche Gesetz beschreibt den Zusammenhang zwischen der Intensität des transmittierten Lichts  und der Intensität des einfallenden Lichts
und der Intensität des einfallenden Lichts  . Die Intensität hat dabei die Einheit Watt pro Quadratmeter
. Die Intensität hat dabei die Einheit Watt pro Quadratmeter
![Rendered by QuickLaTeX.com \left[ \frac{W}{m^2} \right].](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-1c801e2c338b49a6d70fca74045b345a_l3.png)
Die Absorbanz eines Materials für Licht der Wellenlänge  , was auch als Extinktion bezeichnet wird, ist durch das Lambert Beersche Gesetz gegeben
, was auch als Extinktion bezeichnet wird, ist durch das Lambert Beersche Gesetz gegeben

Hierbei repräsentiert  die Konzentration der absorbierenden Substanz in der Flüssigkeit (in mol/m
die Konzentration der absorbierenden Substanz in der Flüssigkeit (in mol/m ),
),  die Weglänge des Lichts im Material (in cm) und
die Weglänge des Lichts im Material (in cm) und  ist der dekadische Extinktionskoeffizient
bei der Wellenlänge
ist der dekadische Extinktionskoeffizient
bei der Wellenlänge  . Der dekadische Extinktionskoeffizient ist eine spezifische Größe des gegebenen absorbierenden Materials.
. Der dekadische Extinktionskoeffizient ist eine spezifische Größe des gegebenen absorbierenden Materials.
Extinktion
Wie im letzten Abschnitt schon kurz erwähnt, ist die Extinktion die Abschwächung einer elektromagnetischen Welle beim Durchgang durch ein Medium. Diese Abschwächung hängt dabei von der Wellenlänge  der Strahlung ab und wird von verschiedenen Vorgängen wie Streuung, Absorption, Beugung und Reflexion verursacht. Angenommen,
der Strahlung ab und wird von verschiedenen Vorgängen wie Streuung, Absorption, Beugung und Reflexion verursacht. Angenommen,  ist die Intensität der einfallenden Strahlung und
ist die Intensität der einfallenden Strahlung und  die Intensität nach dem Durchqueren des Mediums, dann ist die Extinktion gerade der logarithmische Kehrwert des Transmissionsgrades
die Intensität nach dem Durchqueren des Mediums, dann ist die Extinktion gerade der logarithmische Kehrwert des Transmissionsgrades 

Wobei der Transmissionsgrad  gerade die Durchlässigkeit eines Mediums beschreibt.
gerade die Durchlässigkeit eines Mediums beschreibt.
Lambert Beersches Gesetz Herleitung
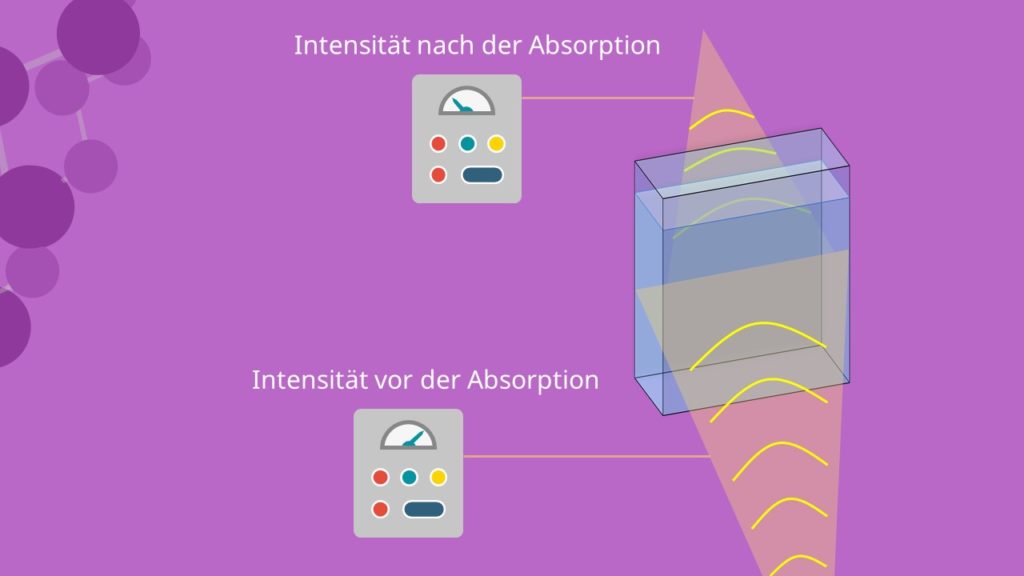
Um das Lambert Beersches Gesetz herzuleiten, geht man von folgender experimenteller Überlegung aus. Man lässt elektromagnetische Strahlung auf eine absorbierende Substanz treffen, die sich in einer Küvette befindet. Dabei misst man die Intensität der Strahlung vor der Substanz und hinter der Substanz. Es zeigt sich hierbei, dass die differentielle Intensität der Strahlung nach dem Durchqueren der Substanz um den Betrag  abgenommen hat. Außerdem ist
abgenommen hat. Außerdem ist  proportional zur Intensität
proportional zur Intensität  , zum Extinktionskoeffizienten
, zum Extinktionskoeffizienten  , der moralen Konzentration
, der moralen Konzentration  und der differentiellen Schichtdicke
und der differentiellen Schichtdicke 

Mit der Trennung der Variablen
kann diese Differentialgleichung unter Verwendung der Anfangsbedingung  gelöst werden
gelöst werden

Damit erhält man folgende Gleichung:

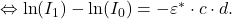
Die Abnahme der Intensität der elektromagnetischen Strahlung beim Durchdringen einer Substanz mit der Konzentration  kann also durch eine Exponentialfunktion beschrieben werden:
kann also durch eine Exponentialfunktion beschrieben werden:



Im Allgemeinen wird die Extinktion und der Extinktionskoeffizient nicht über den natürlichen Logarithmus definiert, sondern über den Logarithmus zur Basis 10. Da der natürliche Logarithmus und der Logarithmus zur Basis 10 linear zusammenhängen, kann man die obere Gleichung einfach in eine Gleichung mit dem Logarithmus zur Basis 10 überführen. Dafür schreiben wir die obere Gleichung zuerst noch einmal um:


Mit  erhält man dann die Gleichung mit dem Logarithmus zur Basis 10:
erhält man dann die Gleichung mit dem Logarithmus zur Basis 10:

Lambert Beersches Gesetz Gültigkeit
Das Lambert Beersches Gesetz ist nicht in allen Situtationen gültig. Deshalb wird im Folgenden aufgezählt, unter welchen Bedingungen das Lambert Beersches Gesetz die Strahlungsintensität richtig beschreibt:
- die absorbierende Substanz muss eine homogene Verteilung aufweisen;
- es darf keine Strahlungskopplung geben;
- die Mehrfachstreuung muss vernachlässigbar sein;
- die Variation des Absorptionskoeffizienten innerhalb des verwendeten Spektralbereichs muss vernachlässigbar sein;
- die Eigenemission muss vernachlässigbar sein, das heißt die transmittierte Strahlungsintensität muss über der Eigenstrahlung liegen;
- die verwendete Substanz darf nur eine geringe Konzentration aufweisen, da bei starker Konzentration Wechselwirkungen auftreten, die zu größeren Abweichungen führen; und
- es sollten keine Interferenzeffekte des Lichts auftreten, sodass die Welleneigenschaft des Lichts vernachlässigbar ist.
Lambert Beersches Gesetz Beispiel und Anwendung
Ein analoges Gesetz zum Lambert Beerschen Gesetz gilt auch für elektromagnetische Strahlung, die sich in dämpfenden Medien verschiedener Art ausbreitet. Aufgeführt seien hier zum Beispiel die Dämpfung von Licht in optischen Medien oder in Lichtwellenleitern. Allgemein drückt man das Gesetz aus durch

Dieses Gesetz beschreibt die Strahlungsleistung nach dem Durchqueren eines Mediums der Dicke  . Dabei ist
. Dabei ist  die Strahlungsleistung vor dem Durchqueren des Mediums und
die Strahlungsleistung vor dem Durchqueren des Mediums und  der Absorptionskoeffizient in der Einheit
der Absorptionskoeffizient in der Einheit  . Hat man beide Intensitäten gemessen, so kann damit auch die Dicke
. Hat man beide Intensitäten gemessen, so kann damit auch die Dicke  des Mediums bestimmt werden.
des Mediums bestimmt werden.
Dieses Gesetz findet in verschiedene Bereichen, wie zum Beispiel bei der Signalübertragung, der Fernerkundung oder der Computertomographie in modifizierter Form Anwendung.
Lichtwellenleiter
Lichtwellenleiter finden Verwendung bei der Übertragung von optische Signale über weite Strecken. Anstatt der oberen Formel, verwendet man in der Signalübertragungstechnik die modifizierte Formel

 beschreibt dabei die Länge des Lichtwellenleiters und
beschreibt dabei die Länge des Lichtwellenleiters und  die Dämpfung in dB/km. Man wählt diese Darstellung in der Nachrichtentechnik, da das Verhältnis von Leistungen im dezimal-logarithmischen Maß (Dezibel) gemessen wird
die Dämpfung in dB/km. Man wählt diese Darstellung in der Nachrichtentechnik, da das Verhältnis von Leistungen im dezimal-logarithmischen Maß (Dezibel) gemessen wird

Fernerkundung und Atmosphäre
Das Lambert Beersches Gesetz findet auch bei der Fernerkundung Anwendung. Insbesondere für die Atmosphäre ist das Gesetz in modifizierter Form gegeben durch

Hierbei steht  für die atmosphärische Masse und
für die atmosphärische Masse und 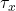 für die optische Dicke des Stoffes
für die optische Dicke des Stoffes  . Somit repräsentiert
. Somit repräsentiert  die optische Dicke der Aerosole,
die optische Dicke der Aerosole,  die optische Dicke der absorbierenden Gase wie Kohlendioxid CO
die optische Dicke der absorbierenden Gase wie Kohlendioxid CO und molekularer Sauerstoff O
und molekularer Sauerstoff O und
und  die optische Dicke von Stickstoffdioxid. Des Weiteren beschreibt
die optische Dicke von Stickstoffdioxid. Des Weiteren beschreibt  die optische Dicke von Wasserstoff,
die optische Dicke von Wasserstoff,  die optische Dicke von Ozon und
die optische Dicke von Ozon und  die Rayleigh-Streuung von molekularem Sauerstoff O
die Rayleigh-Streuung von molekularem Sauerstoff O und von Stickstoff N
und von Stickstoff N .
.
Computertomographie
Die Computertomographie ist ein bildgebendes Verfahren, welches eingesetzt wird, um bestimmte Krankheitsbilder zu erkennen und bestimmte Organe, wie Herz und Lunge, zu beobachten. Auch in der Computertomographie findet das Lambert Beersches Gesetz Anwendung. Mit ihm wird die Abschwächung der Röntgenstrahlung beschrieben. Dabei hängt der Absorptionskoeffizient  von dem Ort
von dem Ort  ab. Denn im menschlichen Körper absorbieren verschiedene Gewebearten unterschiedlich stark die Strahlung. Knochen absorbieren zum Beispiel mehr Strahlung als die Lunge. Die so gemessene Intensität
ab. Denn im menschlichen Körper absorbieren verschiedene Gewebearten unterschiedlich stark die Strahlung. Knochen absorbieren zum Beispiel mehr Strahlung als die Lunge. Die so gemessene Intensität  der Röntgenstrahlung hängt deshalb mit dem Absorptionskoeffizienten über folgendes Integral zusammen
der Röntgenstrahlung hängt deshalb mit dem Absorptionskoeffizienten über folgendes Integral zusammen

wobei  die emittierte Strahlung der Röntgenröhre ist. Bei der Computertomographie erhält man ein Bild, das die Funktion
die emittierte Strahlung der Röntgenröhre ist. Bei der Computertomographie erhält man ein Bild, das die Funktion  in Graustufen darstellt, dabei wird der Absorptionskoeffizient
in Graustufen darstellt, dabei wird der Absorptionskoeffizient  aus der Intensität
aus der Intensität  mit der oberen Formel berechnet.
mit der oberen Formel berechnet.