Video

Quiz

Hier geht's zum Video „Lambert Beersches Gesetz“

Extinktionskoeffizient

Wichtige Inhalte in diesem Video

Extinktionskoeffizient einfach erklärt

Extinktionskoeffizient im Bereich Chemie

Extinktionskoeffizient im Bereich Optik

Du bist beim Lernen gerade über den Extinktionskoeffizient gestolpert und fragst dich, was dieser genau beschreibt und für was er eingesetzt wird. Kein Problem! In diesem Beitrag erklären wir dir, was der Extinktionskoeffizienten ist, wie du seine Einheit bestimmst und ihn berechnen kannst.

Du möchtest kurz ein wenig abschalten und den Extinktionskoeffizienten leicht verständlich erklärt bekommen? Dann schau unser Video dazu an.

Inhaltsübersicht

Extinktionskoeffizient einfach erklärt

im Videozur Stelle im Video springen

Der Extinktionskoeffizient ist ein Maß, das angibt, wie stark sich elektromagnetische Strahlung beim Durchqueren eines Mediums abschwächt.

Merke

Er ist abhängig von der Weglänge, welche die Strahlung im Medium zurücklegt und von der Stoffmengenkonzentration.

Prozesse die zur Abschwächung der Strahlung führen, sind zum Beispiel die Streuung und die Absorption. Der Extinktionskoeffizient tritt häufig in Bezug mit der Photometrie oder der UV/VIS-Spektroskopie auf.

Extinktionskoeffizient im Bereich Chemie

im Videozur Stelle im Video springen

In der Chemie wird der Extinktionskoeffizient $\varepsilon$ auch molarer, dekadischer Extinktionskoeffizient oder molarer Absorptionskoeffizient genannt. Er beschreibt, wie viel Strahlung von einer bestimmten Substanz bei einer Weglänge von 1cm im Medium absorbiert wird. Berechnen lässt er sich mit Hilfe des Lambert Beerschen Gesetzes .

$E_{\lambda} = \varepsilon \cdot c \cdot d$

$\Leftrightarrow \varepsilon = \frac{E_{\lambda}}{c \cdot d}.$

Hierbei ist $E_{\lambda}$ die Extinktion, welche die Abschwächung der Intensität angibt. Sie ist definiert über den Logarithmus des Verhältnisses von der Intensität der einfallenden Strahlung I_0 und der Intensität der ausfallenden Strahlung I_1 . Die Intensität der einfallenden Strahlung wird dabei vor dem Durchqueren des Mediums gemessen und die Intensität der ausfallenden Strahlung nach dem Durchqueren des Mediums. Genaueres findest du in unserem Beitrag zum Lambert Beerschen Gesetz . Des Weiteren repräsentiert die Variable in der oberen Formel die Stoffmengenkonzentration der Lösung und die Schichtdichte der Küvette, in welcher sich die Substanz befindet.

Extinktionskoeffizient Einheit

Da die Stoffmengenkonzentration häufig in der Einheit $\left[ \frac{\mathrm{mol}}{\mathrm{l}}\right]$ angegeben wird und die Dicke der Küvette in $\left[ \mathrm{cm}\right]$ , ergibt sich mit der dimensionslosen Extinktion nach der oberen Formel die Einheit des Extinktionskoeffizienten durch Liter pro Mol und Zentimeter

$\left[ \frac{\mathrm{l}}{\mathrm{mol} \cdot \mathrm{cm}} \right].$

Man kann die Stoffmengenkonzentration aber auch in der Einheit $\left[\frac{\mathrm{mol}}{\mathrm{cm}^3} \right]$ angegeben. Damit ergibt sich für den Extinktionskoeffizienten dann die Einheit

$\left[\frac{\mathrm{cm}^2}{\mathrm{mol}} \right].$

Molarer Extinktionskoeffizient

Der Molare Extinktionskoeffizient ist von verschiedenen Parametern abhängig, wie zum Beispiel von der Wellenlänge der Strahlung oder dem pH-Wert. Deshalb wird er immer in Bezug zur Wellenlänge angegeben.

Extinktionskoeffizient, Molar, Wellenlänge — Molarer Extinktionskoeffizient Wellenlänge

Extinktionskoeffizient im Bereich Optik

im Videozur Stelle im Video springen

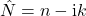Auch im Bereich der Optik tritt der Extinktionskoeffizient auf. Hier ist er über den Imaginärteil des Brechungsindexes $\hat{N} = n-\mathrm{i}k$ definiert. repräsentiert dabei den reellwertigen Brechungsindex. Der Brechungsindex ist allgemein eine dimensionslose Größe, welche das Verhältnis zwischen der Geschwindigkeit von elektromagnetischer Strahlung im Vakuum und der Geschwindigkeit im betrachteten Medium angibt. Betrachtet man eine Grenzfläche zweier verschiedener Medien, die einen unterschiedlichen Brechungsindex haben, dann wird Licht an der Grenzfläche gebrochen und reflektiert. Der Extinktionskoeffizient hängt dabei auch wieder von verschiedenen Faktoren, wie Wellenlänge der Strahlung, Temperatur, Kristallstruktur des Materials und noch mehr ab. Außerdem steht der Extinktionskoeffizient , der reelle Brechungsindex und der Absorptionskoeffizient $\kappa$ miteinander in Relation

$k = n \cdot \kappa.$

Extinktionskoeffizient berechnen

Im Folgenden wird gezeigt, was der imaginäre Brechungsindex physikalisch beschreibt und bewirkt. Dafür betrachten wir ein Beispiel mit ebenen Wellen. Eine ebene Welle kann durch folgende Gleichung beschrieben werden

$E(x,t) = E_0 \cdot e^{\mathrm{i}(\omega t -kx)}.$

Dabei steht $\omega$ für die Frequenz und für die Zeit. Eine ebene Welle beschreibt eine senkrecht zur Ausbreitungsrichtung ausgedehnte Welle im dreidimensionalen Raum. Dabei ist die Wellenfront eine Ebene. Drückt man den Extinktionskoeffizienten mit der Phasengeschwindigkeit aus

$k = \frac{\hat{N} \cdot \omega}{c}$

und setzt dies in die ebene Wellengleichung ein, erhält man

$E(x,t) = E_0 \cdot e^{\mathrm{i}\left(\omega t-\frac{\hat{N}\cdot \omega}{c}x\right) } \quad\quad \text{mit } \hat{N} = n-\mathrm{i}k$

$\Leftrightarrow E(x,t)= E_0\cdot e^{\mathrm{i}\left( \omega t - \frac{n \omega}{c}x+\frac{\mathrm{i}k\omega}{c}x\right)}$

$\Leftrightarrow E(x,t)= E_0 \cdot e^{\mathrm{i}\left(\omega t-\frac{n\omega}{c}x \right)- \frac{k \omega}{c}x}$

$\Leftrightarrow E(x,t)=\underbrace{E_0 \cdot e^{-\frac{k \omega}{c}x}}_{(*)} \cdot e^{\mathrm{i} \left( \omega t- \frac{n \omega }{c}x \right)}.$

Der Term (*) beschreibt dabei die Amplitude der Welle in Abhängigkeit der Eindringtiefe . Hieran kann man sehr gut erkennen, wenn der Extinktionskoeffizient positiv ist, also k>0 , dann nimmt die Amplitude der elektromagnetischen Welle beim Durchqueren des Mediums exponentiell ab.

Quiz zum Thema Extinktionskoeffizient

Extinktionskoeffizient berechnen Beispiel

Angenommen, man betrachtet eine Küvette mit einer Breite von 1cm, in der sich eine Substanz mit der Dichte 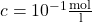$c=10^{-1}\frac{\mathrm{mol}}{\mathrm{l}}$ befindet. Erhält man anschließend durch Messung der Intensität des Lichts vor der Küvette und hinter der Küvette eine Extinktion von $E_{\lambda}= 0,9,$ so lässt sich der Extinktionskoeffizient mit der obigen Formel berechnen durch

$\varepsilon = \frac{E_{\lambda}}{c \cdot d}= \frac{0,9}{10^{-1}\frac{\mathrm{mol}}{\mathrm{l}} \cdot 1\mathrm{cm}}= 9\frac{\mathrm{l}}{\mathrm{mol \cdot cm}}.$

zur Videoseite: Extinktionskoeffizient

Beliebte Inhalte aus dem Bereich Analytische Chemie

Lambert Beersches Gesetz

Extinktionskoeffizient

Massenspektrometer

NMR Spektroskopie

Hallo, leider nutzt du einen AdBlocker.

Auf Studyflix bieten wir dir kostenlos hochwertige Bildung an. Dies können wir nur durch die Unterstützung unserer Werbepartner tun.

Schalte bitte deinen Adblocker für Studyflix aus oder füge uns zu deinen Ausnahmen hinzu. Das tut dir nicht weh und hilft uns weiter.

Danke!
Dein Studyflix-Team

Wenn du nicht weißt, wie du deinen Adblocker deaktivierst oder Studyflix zu den Ausnahmen hinzufügst, findest du hier eine kurze Anleitung. Bitte .