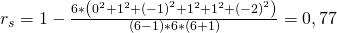Spearman Korrelation
Hier erfährst du alles über die Spearman Korrelation. Nach einer Erklärung der Rangkorrelation nach Spearman erfolgt die Berechnung und die Spearman Korrelation Interpretation.
Bei Rängen denkst du nur an das Treppchen bei einer Siegerehrung? Sieh dir unser Video zur Spearman Rangkorrelation an und erfahre welche Rolle der Rang in der Statistik spielt, ohne diesen langen Artikel lesen zu müssen!
Inhaltsübersicht
Rangkorrelationskoeffizient Spearman
Der Rangkorrelationskoeffizient nach Spearman, welcher auch als Spearmans Rho bezeichnet wird, ist ähnlich wie der Pearson Korrelationskoeffizient eine Methode, um Zusammenhänge zwischen Variablen zu berechnen. Die Korrelation wird anhand zuvor vergebener Ränge berechnet, wobei der genaue Abstand der Datenpunkte nicht relevant ist.
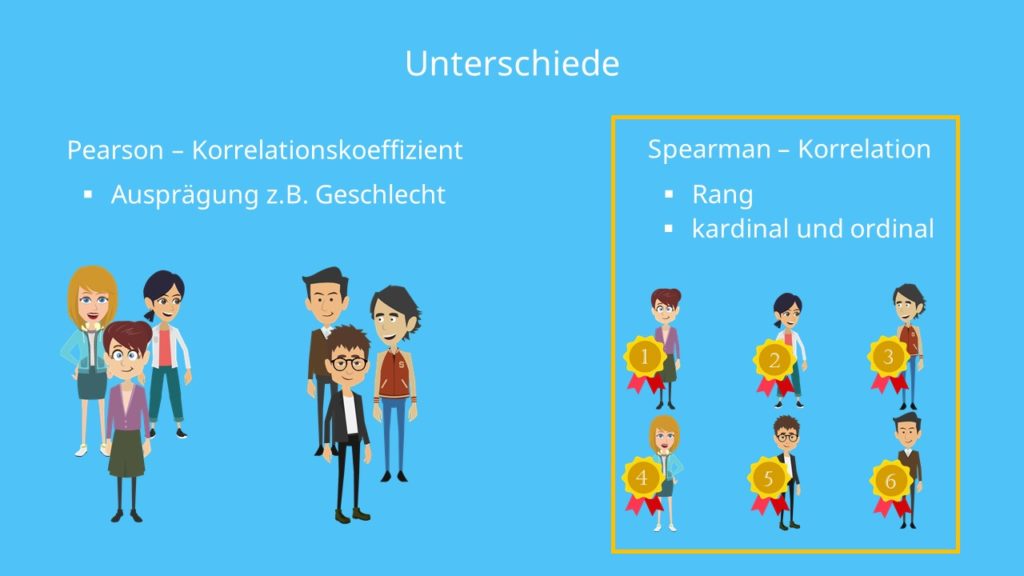
Pearson Korrelation VS. Spearman Korrelation
Der Korrelationskoeffizient nach Spearman verfolgt das gleiche Ziel wie der Pearson Koeffizient. Die Interpretation der Ergebnisse unterscheidet sich ebenfalls nicht. Der grundlegende Unterschied ist allerdings: Während wir den Pearson Korrelationskoeffizient auf Basis der Ausprägungen berechnen, beziehen wir uns bei der Spearman Korrelation auf die Ränge der Ausprägungen. Die absoluten Abstände zwischen den Daten sind also nicht relevant. Das heißt, wir können diesen Koeffizienten sowohl für kardinal-, als auch ordinalskalierte Datensätze berechnen.
Berechnung Rangkorrelation nach Spearman
Rang eins geht an den größten Wert, Rang zwei an den Zweitgrößten und so weiter. Prinzipiell ist es aber egal, ob du dem größten Wert die höchste oder die niedrigste Rangziffer zuordnest.
Wichtig ist nur, dass du einheitlich bleibst und später bei der Interpretation deiner Lösung die richtigen Schlüsse ziehst. Erstmal schauen wir aber, wie man die Spearman Korrelation berechnet.
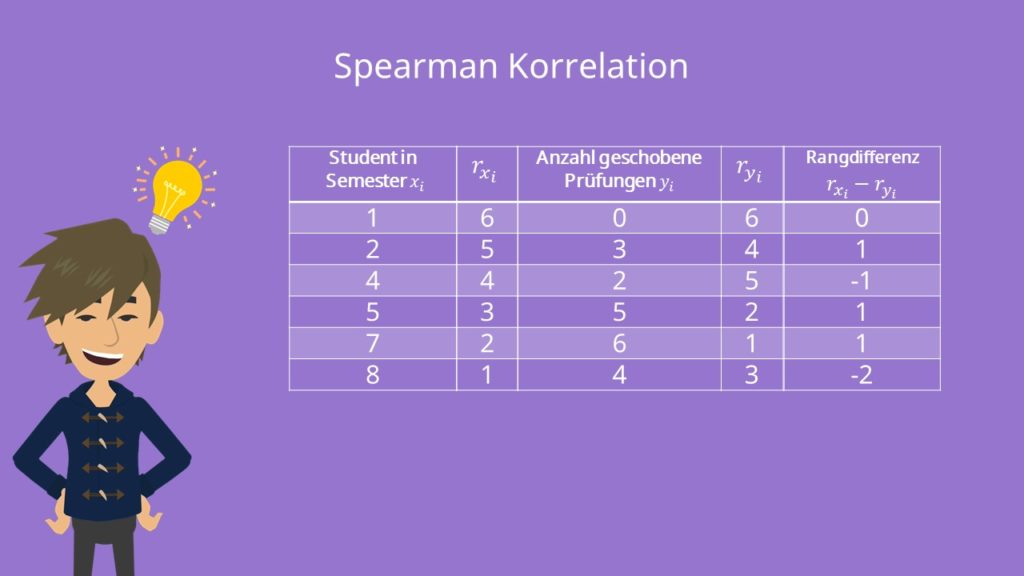
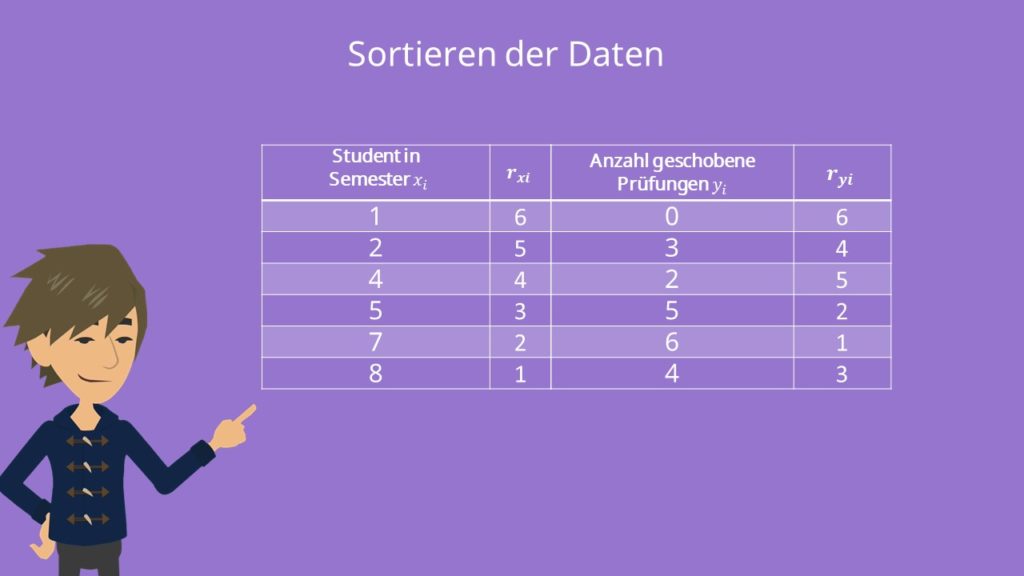
Wir betrachten die Anzahl der geschobenen Prüfungen von sechs verschiedenen Studenten aus sechs verschiedenen Semestern und wollen herausfinden, ob ein Zusammenhang zwischen der Dauer des Studiums und der Anzahl der nicht geschriebenen Prüfungen besteht. Dazu haben wir folgende Datenreihe:
Zuordnung der Rangziffern in der Datenreihe
Wir beginnen mit der letzten Rangziffer, also Rang 6, und vergeben absteigend die Rangziffern für die Semesteranzahl
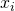 . Anschließend verfahren wir in gleicher Weise für die Anzahl geschobener Prüfungen
. Anschließend verfahren wir in gleicher Weise für die Anzahl geschobener Prüfungen 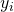 . Dieser Schritt ist noch sehr einfach.
. Dieser Schritt ist noch sehr einfach.
Spearman Korrelation Interpretation
Der Rangkorrelationskoeffitient bei der Spearman Korrelation nimmt im Allgemeinen Werte zwischen -1 im Falle einer negativen Korrelation und +1 im Falle einer positiven Korrelation an, ohne dabei irgendwelche Annahmen über die Verteilungen der Wahrscheinlichkeiten der betrachteten Variablen vorzunehmen. Bei dem Wert 0 liegt keine Korrelation vor. Solltest du also noch nicht wissen, was beispielsweise eine Korrelation von eins bedeutet, empfehlen wir dir das Video Pearson Korrelationskoeffizient anzuschauen.
Sehr gut, aufgrund unserer Berechnungen erhalten wir einen Wert von 0,77. Damit ergibt sich ein stark positiver Zusammenhang zwischen der Dauer des Studiums und der Anzahl der geschobenen Prüfungen!
Aber Achtung, diese Formel für die Spearman Korrelation funktioniert nur, wenn in deinen Daten keine Bindungen auftreten. Das bedeutet, dass jeder x und y Wert nur einmal vorkommen darf.
Alternative Formel zur Berechnung der Rangkorrelation
Eine Formel, die immer funktioniert, zeigen wir dir jetzt. Allerdings wird sie nicht an jeder Uni gelehrt und ist nicht zwingend relevant für dich.
Hast du zum Beispiel folgende x-Werte und Ränge:
Wir haben also Rang eins plus Rang zwei durch 2 geteilt, also den Mittelwert berechnet und ihn an beide x-Werte vergeben.
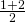
Um nun die Korrelation zu berechnen, benötigen wir eine neue Formel:
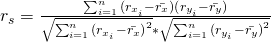
Aufmerksamen Zuschauern wird die Formel bereits bekannt vorkommen. Na, kommst du drauf? Richtig! Sie ist der Formel des Pearson Korrelationskoeffizienten sehr ähnlich. Nur rechnen wir wieder mit den Rängen unserer Daten.
Ansonsten war‘s das aber schon! Wenn du immer auf die richtige Vergabe der Ränge achtest und beide Formeln im Kopf hast, sollte es kein Problem mehr sein, auf die korrekte Lösung zu kommen.


![Rendered by QuickLaTeX.com r_s=1-\frac{6\sum_{i=1}^{n}{(r_{x_i}-r_{y_i})}^2}{(n-1)\ast n\ast (n+1)}\in\ \left[-1;1\right]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-925f08fd33e0cf12c88d2fea1a957e74_l3.png)