Integralrechnung einfach erklärt
Die Integralrechnung ist ein wichtiges Teilgebiet der Analysis und hängt eng mit der Differentialrechnung zusammen. Um was es bei der Integralrechnung genau geht, erfährst du hier und in unserem Video!
Inhaltsübersicht
Integralrechnung einfach erklärt
Die Integralrechnung hilft dir, Flächeninhalte zwischen der x-Achse und einer Funktion auszurechnen.
Dafür brauchst du zuerst die sogenannte Stammfunktion. Wie du die berechnest, erfährst du jetzt.
Danach lernst du Schritt für Schritt, wie du die Integralrechnung bei Flächeninhalten und Anwendungsaufgaben nutzen kannst.
Stammfunktionen
Bevor du ein Integral bestimmen kannst, musst du die Stammfunktion F(x) ermitteln. Schau dir zum Beispiel
f(x) = 2x
an. F(x) ist eine Funktion, die abgeleitet f(x) ergibt. Deshalb ist hier
F(x) = x2
Für F(x) gilt immer: F'(x) = f(x)
Das Bilden einer Stammfunktion ist also das Gegenteil vom Ableiten. Deshalb nennst du es manchmal auch Aufleiten .
Achtung! Du hast gesehen, dass F(x) = x2 eine Stammfunktion von f(x) = 2x ist, weil x2 abgeleitet 2x ergibt. Aber auch
- x2 + 1,
- x2 + 5 und
- x2 – 5
ergeben abgleitet 2x! Du kannst also hinter x2 noch eine beliebige Zahl schreiben. Die bezeichnest du allgemein mit c. Alle Stammfunktionen von f(x) = 2x haben also die Form
x2 + c
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Wichtige Beispiele fürs Aufleiten
Am wichtigsten ist, dass du Potenzfunktionen aufleiten kannst, zum Beispiel x3 oder 5x2. Dafür musst du nur zwei Schritte beachten:
- Erhöhe die Hochzahl um 1: x3 → x4
- Schreibe den Bruch
 vor die Potenz:
vor die Potenz: 
Weitere wichtige Beispiele findest du in der Tabelle.
| f(x) | F(x) |
| f(x) = 3x2 | F(x) = x3 |
| f(x) = 4x3 + 5x | F(x) = x4 + 2,5x2 |
| f(x) = 1 | F(x) = x |
| f(x) = 2 | F(x) = 2x |
| f(x) = ex | F(x) = ex |
| f(x) = sin(x) | F(x) = -cos(x) |
| f(x) = cos(x) | F(x) = sin(x) |
| f(x) = 1/x | F(x) = ln(x) |
Unbestimmtes Integral
Die Menge aller Stammfunktionen von einer Funktion f(x) kannst du mit dem unbestimmten Integral angeben. Du brauchst dafür das Integrationszeichen ∫. Schau dir zum Beispiel an, wie du das unbestimmte Integral von 2x aufschreiben kannst:
![Rendered by QuickLaTeX.com \[\int 2x \, dx = x^2 + \textcolor{blue}{c}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-9963b2db6b0d1a55c5a7065284c3a439_l3.png)
Allgemein kannst du dir merken:
![Rendered by QuickLaTeX.com \[\int \textcolor{red}{f(x)} \, \textcolor{teal}{dx} = F(x) + \textcolor{blue}{c}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-1606292ba7019ff7da86f043fb973fb4_l3.png)
f(x) hießt Integrand und dx Differential. Das Differential musst du immer hinter f(x) schreiben! Das x nennst du Integrationsvariable und c ist die Integrationskonstante.
Bestimmtes Integral
Mit dem unbestimmten Integral kannst du auch ein bestimmtes Integral berechnen. Dann stehen oben und unten an deinem Integral Zahlen, die sogenannten Integrationsgrenzen. Hier siehst du ein Beispiel:
![Rendered by QuickLaTeX.com \[\int\limits_{\textcolor{orange}{0}}^{\textcolor{orange}{1}} 2x \, dx\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-53261a6aef3d5354714b82da5cf63b6c_l3.png)
Aber wie kannst du das Integral berechnen? Allgemein lautet die Formel für die Integralrechnung:
![Rendered by QuickLaTeX.com \[\int\limits_a^b f(x) \, dx = \biggl[F(x)\biggr]\limits_a^b = F(b) - F(a) \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-b886da48a9bc2c0acbf2d8db50325e37_l3.png)
In deinem Beispiel rechnest du also:
![Rendered by QuickLaTeX.com \[\int\limits_{\textcolor{orange}{0}}^{\textcolor{orange}{1}} 2x \,dx = \biggl[x^2\biggr]\limits_{\textcolor{orange}{0}}^{\textcolor{orange}{1}} = {\textcolor{orange}{1}}^2 - {\textcolor{orange}{0}}^2 = 1 \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-ebb2538cda553f7eb743dfb5970b70a9_l3.png)
Um ein bestimmtes Integral zu berechnen, gehst du so vor:
- Schritt 1: Berechne die Stammfunktion F(x) und schreibe Sie in eckige Klammern
- Schritt 2: Setze die Integrationsgrenzen a und b in F(x) ein.
-
Schritt 3: Ziehe F(a) von F(b) ab.
Anwendungsaufgabe Integralrechnung: Beispiel
Oft musst du in der Integralrechnung Anwendungsaufgaben bearbeiten. Schau dir dazu ein Beispiel an:
In einen leeren Behälter fließt Wasser. Die Zuflussrate in Litern pro Minute wird durch die Funktion f(x) = -t2 + 20t angegeben. t ist dabei die Zeit in Minuten. Wie viel Wasser ist nach 10 Minuten im Behälter?
Lösung
Wenn du eine Änderungsrate (z. B. eine Zuflussrate) gegeben hast, berechnest du die Gesamtmenge immer mithilfe von Integralrechnung. Die Integrationsgrenzen sind durch das Zeitintervall gegeben, hier als 0 und 10:
![Rendered by QuickLaTeX.com \begin{align*} \int\limits_{\textcolor{orange}{0}}^{\textcolor{orange}{10}} -x^2+20x\, dx &= \biggl[-\frac{1}{3}x^3 +10x^2 \biggr]\limits_{\textcolor{orange}{0}}^{\textcolor{orange}{10}} \\ &= -\frac{1}{3}\cdot 10^3 +10\cdot 10^2 -(-\frac{1}{3}\cdot 0^3 +10\cdot 0^2) = \frac{2000}{3} \approx 666,7 \end{align*}](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-b61da1598686862013cc4737c113ebbe_l3.png)
Es sind also nach 10 Minuten 666,7 Liter Wasser im Behälter.
Flächenberechnung durch Integralrechnung
Mithilfe der Integralrechnung kannst du den Flächeninhalt zwischen der Funktion und der x-Achse innerhalb der Integrationsgrenzen berechnen. Das Integral  gibt dir also den Flächeninhalt zwischen f(x) = 2x und der x-Achse im Intervall [0,2] an.
gibt dir also den Flächeninhalt zwischen f(x) = 2x und der x-Achse im Intervall [0,2] an.
In dem Beispiel waren deine Integrationsgrenzen vorgegeben. Wenn du den Flächeninhalt berechnen willst, den der Graph mit der x-Achse einschließt, musst du sie aber selbst herausfinden. Dann gehst du so vor:
- Schritt 1: Berechne die Nullstellen deiner Funktion.
- Schritt 2: Schreibe das bestimmte Integral auf. Die Nullstellen sind die Integrationsgrenzen.
- Schritt 3: Integral berechnen.
Achtung! Wenn du mehr als zwei Nullstellen hast, musst du auch mehr als ein Integral ausrechnen. Hast du zum Beispiel die Nullstellen 2, 3 und 5, dann berechnest du ein Integral von 2 bis 3 und eines von 3 und 5.
Schau dir gleich zwei Beispiele zu Flächeninhalten in der Integralrechnung an!
Flächenberechnung Beispiel 1
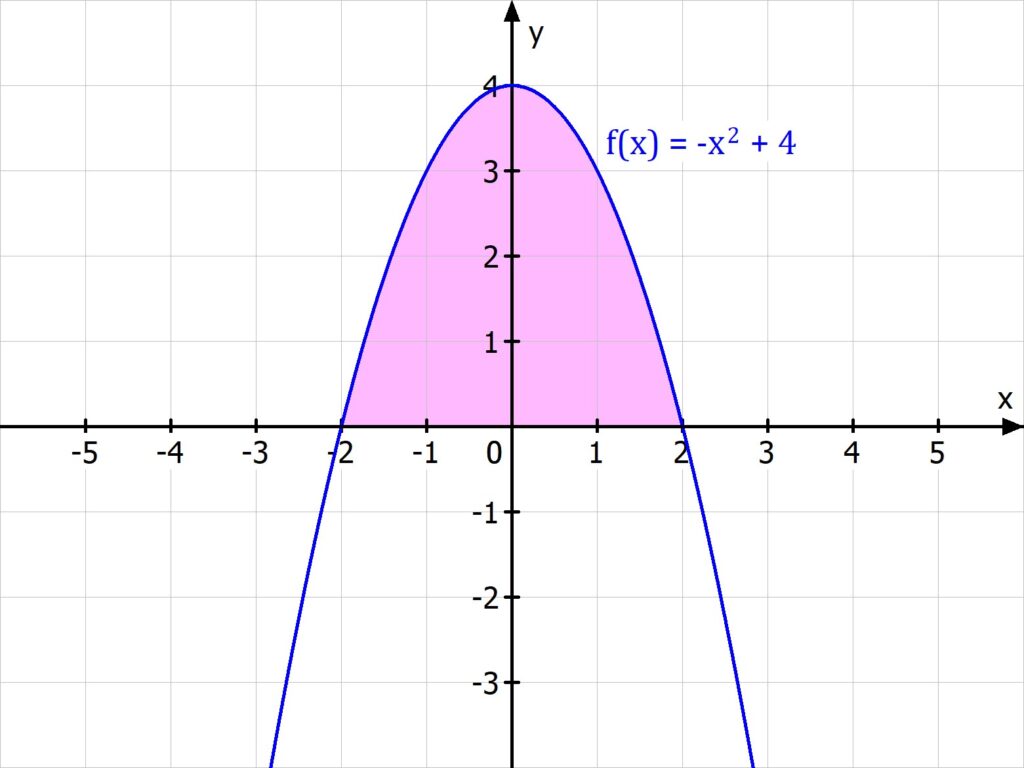
Du willst die Fläche zwischen f(x) = -x2 + 4 und der x-Achse mit dem Integral berechnen.
- Schritt 1: Berechne die Nullstellen. Du erhältst x1 = -2 und x2 = 2.
-
Schritt 2: Schreibe das bestimmte Integral auf:
![Rendered by QuickLaTeX.com \[\int\limits_{\textcolor{orange}{-2}}^{\textcolor{orange}{2}} -x^2+4\, dx\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-9779d848b7211b948e5d60cbed3508fd_l3.png)
-
Schritt 3: Integral lösen.
![Rendered by QuickLaTeX.com \[\int\limits_{\textcolor{orange}{-2}}^{\textcolor{orange}{2}} -x^2+4\, dx = \biggl[-\frac{1}{3} x^3 + 4x \biggr]\limits_{\textcolor{orange}{-2}}^{\textcolor{orange}{2}} = -\frac{1}{3} \cdot 2^3 + 4 \cdot 2 - (-\frac{1}{3} \cdot (-2)^3 + 4 \cdot (-2)) = \frac{32}{3}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-2f368e7430a30c30f646809f6480442e_l3.png)
Der Flächeninhalt zwischen der Funktion und der x-Achse beträgt also 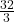 .
.
Flächenberechnung Beispiel 2
Schau dir noch ein Beispiel mit mehr als zwei Nullstellen an: f(x) = x3 – 4x. Bestimme den Flächeninhalt A zwischen dem Graphen und der x-Achse.
- Schritt 1: Berechne die Nullstellen. Du erhältst x1 = -2 und x2 = 0 und x3 = 2.
-
Schritt 2: Schreibe zwei Integralrechnungen auf:
und![Rendered by QuickLaTeX.com \[A_1 = \int\limits_{\textcolor{orange}{-2}}^{\textcolor{orange}{0}} x^3-4x \,dx\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-ecaa157989af3c5008551552343409af_l3.png)
![Rendered by QuickLaTeX.com \[A_2 = \int\limits_{\textcolor{orange}{0}}^{\textcolor{orange}{2}} x^3-4x \,dx\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-7e3fdba7e67033d5a376191f147de767_l3.png)
- Schritt 3: Integral bestimmen.
![Rendered by QuickLaTeX.com \begin{align*} A_1 = \int\limits_{\textcolor{orange}{-2}}^{\textcolor{orange}{0}} x^3-4x \,dx &= \biggl[\frac{1}{4} x^4 - 2x^2 \biggr]\limits_{\textcolor{orange}{-2}}^{\textcolor{orange}{0}} \\ &= \frac{1}{4} \cdot 0^4 - 2 \cdot 0^2 - (\frac{1}{4} \cdot (-2)^4 - 2\cdot (-2)^2) = 4 \end{align*}](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-7b0557e532c830f470c28b0fbc617253_l3.png)
![Rendered by QuickLaTeX.com \[A_2 = \int\limits_{\textcolor{orange}{0}}^{\textcolor{orange}{2}} x^3-4x\, dx = \biggl[\frac{1}{4} x^4 - 2x^2 \biggr]\limits_{\textcolor{orange}{0}}^{\textcolor{orange}{2}} = \frac{1}{4} \cdot 2^4 - 2 \cdot 2^2 - (\frac{1}{4} \cdot 0^4 - 2\cdot 0^2) = -4\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-22508737d433784e5290328cbac0697e_l3.png)
Für A2 kommt also eine negative Zahl heraus. Weil ein Flächeninhalt aber nicht negativ sein kann, musst du die positive Zahl davon betrachten, also 4. Der Flächeninhalt zwischen dem Graphen und der x-Achse ist dann:
A = A1 + A2 = 4 + 4 = 8
Flächen zwischen zwei Graphen
Wenn du die Fläche zwischen zwei Graphen f(x) und g(x) berechnen sollst, gehst du so vor:
- Schritt 1: Berechne die Schnittpunkte der beiden Funktionen f(x) und g(x).
- Schritt 2: Stelle das Integral von f(x)-g(x) mit den Schnittpunkten als Integrationsgrenzen auf.
- Schritt 3: Integral berechnen.
Schau dir auch dazu ein Beispiel an.
Fläche zwischen Graphen: Beispiel
Du hast die Funktionen f(x) = -x2 + 4 und g(x) = 2x2 + 1 gegeben und sollst die Fläche dazwischen ausrechnen.
- Schritt 1: Berechne die Schnittpunkte. Dazu setzt du die beiden Funktionen gleich und löst das nach x auf. Du erhältst x1 = -1 und x2 = 1.
-
Schritt 2: Berechne zuerst f(x) – g(x) und stelle damit die Integralrechnung auf.
![Rendered by QuickLaTeX.com \[f(x) - g(x) = -x^2+4-(2x^2+1)=-x^2+4-2x^2-1=\textcolor{red}{-3x^2+3}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-43892a2892cb0af279903efd9423d045_l3.png)
![Rendered by QuickLaTeX.com \[\implies \int\limits_{\textcolor{orange}{-1}}^{\textcolor{orange}{1}} \textcolor{red}{-3x^2+3} \,dx\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-a3391e45756dd1be82ac24315d565e0c_l3.png)
- Schritt 3: Integral bestimmen.
![Rendered by QuickLaTeX.com \[\int\limits_{\textcolor{orange}{-1}}^{\textcolor{orange}{1}} \textcolor{red}{-3x^2+3} \, dx = \biggl[\textcolor{red}{-x^3+3x} \biggr]\limits_{\textcolor{orange}{-1}}^{\textcolor{orange}{1}} = -1^3+3 \cdot 1 - (-(-1)^3+3 \cdot (-1)) = 4 \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-dd12947b6381f51a00b772c3f49edc56_l3.png)
Integrationsregeln
Wie auch beim Ableiten musst du bei der Integralrechnung bestimmte Integrationsregeln beachten. Hier siehst du die wichtigsten auf einen Blick.
Die häufigste Regel in der Integralrechnung ist die Potenzregel. Damit kannst du Potenzen wie x3 oder 5x2 aufleiten. Du hast sie schon bei den Stammfunktionen kennengelernt.
![Rendered by QuickLaTeX.com \[\int x^n \,dx = \frac{1}{n+1}x^{n+1}+c\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-517a4577c6852c68398167f891ddae0b_l3.png)
Die Faktorregel ist die einfachste Integrationsregel. Du benutzt sie, wenn vor deiner Funktion eine Zahl mit Mal dahinter steht, z. B. 2 • ex. Du kannst dann die Zahl einfach vor das Integral ziehen:
![Rendered by QuickLaTeX.com \[ \int c \cdot f(x) \,dx= c \cdot \int f(x)dx \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-75f86e07cb0da124ad003139295faf9d_l3.png)
Die dritte der Integrationsregeln ist die Summenregel. Du verwendest sie immer, wenn in der Integralrechnung eine Summe vorkommt, zum Beispiel in x2 + 4. Du kannst dann die verschiedenen Teile der Summe einzeln integrieren :
![Rendered by QuickLaTeX.com \[\int f(x)+g(x) \,dx = \int f(x) dx + \int g(x) dx\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-1eadb0e2db1fd65d50b06e0ec0cf014d_l3.png)
Ganz ähnlich wie die Summenregel funktioniert auch die Differenzregel:
![Rendered by QuickLaTeX.com \[\int f(x)-g(x) \,dx = \int f(x) dx - \int g(x)\, dx \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-5d9a70aea3b54a1b76442b98a6c380eb_l3.png)
Wenn du Beispiele zu den einzelnen Regeln sehen möchtest, schau dir unser Video zu den Integrationsregeln an.
Für einige Funktionen gibt es auch noch separate Integrationsregeln. Wenn du wissen willst, wie du e-Funktion integrierst, dann schau hier vorbei!
Integralfunktion
Du hast schon gesehen, dass du für ein Integral unterschiedliche Integrationsgrenzen wählen kannst. Lass jetzt einmal die untere Grenze fest, zum Beispiel bei 0, und setze für die obere eine Variable ein, beispielsweise x. Die Integrationsvariable nennst du dann t anstatt x — sonst kommt das x ja doppelt vor.
Dadurch entsteht eine neue Funktion in Abhängigkeit von der oberen Grenze. Du nennst sie Integralfunktion . Die feste untere Grenze bezeichnest du allgemein mit a.
![Rendered by QuickLaTeX.com \[F(x) = \int_a^{\textcolor{orange}{x}} f(t) \,dt \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-ae5d95c439d8f8d2d372e70fd6f4fcec_l3.png)
Jetzt siehst du auch, warum du die Integrationsvariable t nennen musst — die Variable x ist schon für die obere Grenze verbraucht!
Du willst noch detaillierteres Wissen zur Integralrechnung? Dann schau dir auch unseren Artikel für Fortgeschrittene
dazu an!
Expertenwissen: Rotationskörper
Du erhältst einen Rotationskörper, wenn du eine Fläche (z. B. ein Rechteck) um eine Achse im Koordinatensystem herumdrehst. Das Volumen von einem solchen Rotationskörper und seine Mantelfläche kannst du mit dem Integral ausrechnen. Alle wichtigen Formeln und viele Beispiele dazu findest du in diesem Video .
Merke: Die Formeln für die Rotation um die x-Achse und die Rotation um die y-Achse in der Integralrechnung sind unterschiedlich! Pass auf, dass du die beiden nicht verwechselst!
Expertenwissen: Uneigentliches Integral
Ein uneigentliches Integral ist ein Integral, bei dem die Grenzen kritische Werte enthalten. Das bedeutet, dass dort eine Zahl oder ein Zeichen steht, dass du nicht einfach in die Funktion einsetzen kannst. Dabei gibt es zwei Fälle:
- Die Integrationsgrenzen sind unbeschränkt, d. h.
 oder
oder 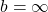
-
 ist an den Integrationsgrenzen nicht definiert. Du darfst also deine Grenze nicht in die Funktion einsetzen.
ist an den Integrationsgrenzen nicht definiert. Du darfst also deine Grenze nicht in die Funktion einsetzen.
Bei der Berechnung eines uneigentlichen Integrals an seiner kritischen Grenze machst du Folgendes:
Anleitung: Uneigentliche Integrale lösen
Schritt 1: Ersetze die kritische Grenze b durch eine Variable 

Schritt 2: Berechne das Integral in Abhängigkeit von 
![Rendered by QuickLaTeX.com A(\beta) :=\int \limits_{a}^{\beta} f(x)dx = \left[F(x)\right]_{a}^{\beta}](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-eb8f39a4d4fbc83da8df3d6495c26f1a_l3.png)
Schritt 3: Bestimme, falls vorhanden, den Grenzwert

Merke: Wenn du bei einem uneigentlichen Integral zwei kritische Grenzen hast, musst du es aufteilen und beide Integrale einzeln berechnen. Hier findest du weitere Aufgaben, um das Thema noch besser zu verstehen.
Expertenwissen: Partielle Integration
Wenn deine Integralrechnung ein Produkt enthält, kannst du beim Integrale lösen eine spezielle Regel verwenden: die partielle Integration. Du kannst sie dir vorstellen wie die Produktregel vom Ableiten, nur umgekehrt. Die Erklärung und viele Beispiele lernst du in einem separaten Video kennen. Hier siehst du schonmal die Formel auf einem Blick:
![Rendered by QuickLaTeX.com \[\int \limits_a^b f'(x) \cdot g(x) \,dx = \biggl[f(x) \cdot g(x)\biggr]\limits_a^b -\int\limits_a^b f(x)\cdot g'(x) \,dx \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-2032bdd68ae78ace38c9f9d512256a35_l3.png)
Beispiel
Wir wollen  mithilfe von partieller Integration berechnen. Hier ist
mithilfe von partieller Integration berechnen. Hier ist  und
und  . Damit gilt:
. Damit gilt:
![Rendered by QuickLaTeX.com \int\limits_0^\pi x\cdot \sin(x)\,dx = \biggl[-x\cdot \cos(x)\biggr]\limits_0^\pi - \int\limits_0^\pi - \cos(x) dx = \pi +\sin(\pi)-\sin(0)=\pi.](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-ac270e6508fc46cf9126c081d74079e8_l3.png)
Merke: Manchmal kann es sein, dass du bei einer Integralrechnung mehrfach partiell integrieren musst.
Merke: Es ist wichtig, dass du  und
und  passend wählst. Die Merkhilfe LIATE erklären wir dir hier
ausführlich.
passend wählst. Die Merkhilfe LIATE erklären wir dir hier
ausführlich.
Expertenwissen: Integration durch Substitution
Alle wichtigen Infos zu Integrationsregeln zur Substitution findest du in einem eigenen Video.
Die Substitutionsregel ähnelt der Kettenregel
beim Ableiten. Du verwendest sie nämlich dann, wenn du eine innere Funktion  und eine äußere Funktion
und eine äußere Funktion  gegeben hast, d. h. wenn
gegeben hast, d. h. wenn  . Dann substituierst (ersetzt) du
. Dann substituierst (ersetzt) du  und erhältst folgende Formel:
und erhältst folgende Formel:
![Rendered by QuickLaTeX.com \[\int\limits_a^b u(v(x))\cdot v'(x) = \int\limit_{v(a)}^{v(b)} u(y)\,dy \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-2bfdb112817cd647657c04b0fbcf8429_l3.png)
Beispiel
Du suchst die Lösung des Integrals  . Dafür substituierst du
. Dafür substituierst du  und bekommst durch Ableiten und Umstellen
und bekommst durch Ableiten und Umstellen  . Wenn du das in die Integralrechnung einsetzt und noch die Integrationsgrenzen anpasst, erhältst du:
. Wenn du das in die Integralrechnung einsetzt und noch die Integrationsgrenzen anpasst, erhältst du:
![Rendered by QuickLaTeX.com \[\int\limits_0^{\frac{\pi}{2}} \sin(2x)dx=\int\limits_0^\pi \sin(y)\cdot\frac{1}{2}dy = \biggl[\frac{-\cos(y)}{2}\biggr]\limits_0^\pi = 1 \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-c4af603089cb99e7c9fd803a3bfcaba6_l3.png)
Merke: Vergiss nicht, deine Integrationsgrenzen anzupassen, und das dx richtig zu ersetzen!
Expertenwissen: Mittelwertsatz der Integralrechnung
Ein wichtiger Satz in der Integralrechnung ist der Mittelwertsatz der Integralrechnung. Manchmal nennst du ihn auch Cauchyschen Mittelwertsatz. Mithilfe des Mittelwertsatzes kannst du Integrale abschätzen, ohne sie exakt auszurechnen.
In der allgemeinen Fassung besagt der Mittelwertsatz der Integralrechnung, dass für ein stetiges ![Rendered by QuickLaTeX.com f:[a,b] \longrightarrow \mathbb{R}](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-53b3ffcd427ee67944ee48bf4315897a_l3.png) und ein integrierbares
und ein integrierbares ![Rendered by QuickLaTeX.com g:[a,b] \longrightarrow \mathbb{R}](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-db6815fd0acdc216a70ab0e8392d2025_l3.png) ohne Vorzeichenwechsel ein
ohne Vorzeichenwechsel ein ![Rendered by QuickLaTeX.com \xi \in [a,b]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-c4f2ca3b42c3af09dc8fede13ef649b0_l3.png) existiert, sodass
existiert, sodass
![Rendered by QuickLaTeX.com \[\int\limits_a^b f(x)g(x)\, dx = f(\xi)\int\limits_a^b g(x)\, dx \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-05698a163dd2fa757970d58651b9ab5a_l3.png)
Für den Spezialfall g=1 ergibt sich insbesondere:
![Rendered by QuickLaTeX.com \[ \int\limits_a^b f(x)\, dx = f(\xi)(b-a) \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-528cf7cdb130d79d63ff3d05dc5ce562_l3.png)
Geometrisch kannst du diesen „ersten Mittelwertsatz der Integralrechnung“ so interpretieren, dass du zu jedem Flächeninhalt, den  und die x-Achse einschließen, ein entsprechendes Rechteck mit derselben Fläche finden kannst.
und die x-Achse einschließen, ein entsprechendes Rechteck mit derselben Fläche finden kannst.
Das hilft dir vor allem dann, wenn du den durchschnittlichen Wert der Funktion im Intervall ![Rendered by QuickLaTeX.com [a,b]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-b7e4beaceae66bed938a06185209134a_l3.png) bestimmen willst. Der ist nämlich gerade
bestimmen willst. Der ist nämlich gerade  ! Wenn du also den Durchschnitt aller y-Werte im Intervall
! Wenn du also den Durchschnitt aller y-Werte im Intervall ![Rendered by QuickLaTeX.com [a,b]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-b7e4beaceae66bed938a06185209134a_l3.png) ermitteln sollst, berechnest du
ermitteln sollst, berechnest du
![Rendered by QuickLaTeX.com \[f(\xi) = \frac{1}{b-a}\int\limits_a^b f(x)\,dx = \frac{1}{b-a}\left[F(b) - F(a)\right] \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-f79ef24839e01ae84f28a62063e6a5f3_l3.png)
Merke: Du solltest immer aufpassen, dass g(x) im Intervall [a,b] keinen Vorzeichenwechsel hat, d. h. dass ![Rendered by QuickLaTeX.com g(x) < 0\quad \forall x \in [a,b]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-fd2cae3241c372f2cee868e90dfe6183_l3.png) oder
oder ![Rendered by QuickLaTeX.com g(x) > 0 \quad\forall x \in [a,b]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-eda00198c1d1719ba9c3c5ba62120bbf_l3.png) . Ist das nicht der Fall, kannst du den Mittelwertsatz der Integralrechnung nicht anwenden!
. Ist das nicht der Fall, kannst du den Mittelwertsatz der Integralrechnung nicht anwenden!
Expertenwissen: Kurvenintegrale
Du kannst jetzt schon Integrale von reellen Funktionen ermitteln. Mit dem Kurvenintegral
kannst du auch über Funktionen integrieren, deren Definitionsmenge  eine Teilmenge des
eine Teilmenge des  ist. Du integrierst dann entlang der Kurve
ist. Du integrierst dann entlang der Kurve  , die diese Teilmenge umfasst.
, die diese Teilmenge umfasst.
Kurvenintegrale 1. Art: Darunter verstehst du Kurvenintegrale einer skalaren Funktion  . Das ist eine Zuordnung von jedem Wert
. Das ist eine Zuordnung von jedem Wert  zu einer reellen Zahl
zu einer reellen Zahl  .
.
Betrachte die offene Teilmenge  und die Parametrisierung einer stückweise stetig differenzierbaren Kurve
und die Parametrisierung einer stückweise stetig differenzierbaren Kurve ![Rendered by QuickLaTeX.com \gamma:[a,b]\rightarrow \mathbb{R}](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-a6012a63f9060ef89fbb4daeda0beac9_l3.png) . Dann nennst du
. Dann nennst du

das Kurvenintegral 1. Art von  längs der Kurve
längs der Kurve  .
.
Analog dazu existiert in der Integralrechnung das Kurvenintegral 2. Art für vektorwertige Funktionen. Genaueres dazu erklären wir dir hier . Im Folgenden siehst du nochmal das Vorgehen bei Kurvenintegralen auf einen Blick:
Anleitung: Kurvenintegrale lösen
Schritt 1: Parametrisiere die Kurve und setze sie in f ein.
Schritt 2: Bestimme das Bogenelement ds. Es kann je nach Art des Kurvenintegrals skalar oder vektorwertig sein.
Schritt 3: Berechne das Kurvenintegral.
Integralrechnung einfach erklärt — häufigste Fragen
(ausklappen)
Integralrechnung einfach erklärt — häufigste Fragen
(ausklappen)-
Wie erkenne ich schnell, ob ich Substitution oder partielle Integration brauche?Substitution passt meist bei Verkettungen, partielle Integration bei Produkten. Bei Substitution findest du oft eine innere Funktion v(x) und (fast) ihre Ableitung v'(x) als Faktor. Bei partieller Integration steht ein „hartes“ Produkt ohne passende innere Ableitung, z. B. x·sin(x).
-
Wie berechne ich den Flächeninhalt richtig, wenn der Graph zwischen den Grenzen auch unter der x-Achse liegt?Dann darfst du das bestimmte Integral nicht direkt als Flächeninhalt übernehmen, sondern brauchst Beträge bzw. Teilintervalle. Teile das Intervall an den Nullstellen auf und berechne jeden Abschnitt separat. Abschnitte unter der x-Achse liefern negative Integrale, deren Betrag du zur Fläche addierst.
-
Welche typischen Fehler passieren beim bestimmten Integral beim Einsetzen von Grenzen?Häufig wird die Reihenfolge verwechselt: Es gilt immer
 , nicht umgekehrt. Außerdem werden Klammern vergessen, wenn
, nicht umgekehrt. Außerdem werden Klammern vergessen, wenn  abgezogen wird, besonders bei negativen Werten. Ein weiterer Fehler ist, beim Einsetzen Potenzen oder Vorzeichen falsch zu berechnen, etwa
abgezogen wird, besonders bei negativen Werten. Ein weiterer Fehler ist, beim Einsetzen Potenzen oder Vorzeichen falsch zu berechnen, etwa  statt
statt  .
.
-
Warum muss ich bei der Integralfunktion eine andere Variable als x im Integral nehmen?Du brauchst eine andere Variable, damit nicht dieselbe Variable gleichzeitig Grenze und Integrationsvariable ist. In
 ist x nur die obere Grenze, und t ist eine „Platzhaltervariable“ im Integral. So bleibt klar, worüber integriert wird.
ist x nur die obere Grenze, und t ist eine „Platzhaltervariable“ im Integral. So bleibt klar, worüber integriert wird.
-
Wie prüfe ich bei einem uneigentlichen Integral, ob es überhaupt einen endlichen Wert hat?Ein uneigentliches Integral hat nur dann einen endlichen Wert, wenn der passende Grenzwert existiert und endlich ist. Ersetze die kritische Grenze durch eine Variable (z. B.
 ), berechne
), berechne  und prüfe
und prüfe  . Gibt es keinen endlichen Grenzwert, divergiert das Integral.
. Gibt es keinen endlichen Grenzwert, divergiert das Integral.
Aufleiten
Wenn du noch mehr Übung beim Aufleiten brauchst, schau dir gleich noch unser Video dazu an!