Video anzeigen

Hier geht's zum Video „Wurzelfunktion“

Potenzfunktionen

Wichtige Inhalte in diesem Video

Potenzfunktionen einfach erklärt

Potenzfunktionen mit positivem Exponenten

Gerader Exponent

Ungerader Exponent

Potenzfunktionen mit negativem Exponenten

Gerader Exponent

Ungerader Exponent

Potenzfunktionen mit Bruch als Exponent

In diesem Artikel erklären wir dir alles Wichtige zu den Potenzfunktionen. Dabei unterscheiden wir zwischen Potenzfunktionen mit positivem und negativem Exponenten und erklären dir auch, welchen Unterschied es macht, wenn die Potenz gerade oder ungerade ist.

Du möchtest das Thema schnell verstehen? Dann ist unser Video genau das Richtige für dich.

Inhaltsübersicht

Potenzfunktionen einfach erklärt

zur Stelle im Video springen

(00:13)

Potenzfunktionen sind Funktionen, die einem x-Wert seine n-te Potenz zuordnen, das heißt

Funktionsgleichung von Potenzfunktionen

f(x)=ax^n mit $a \in \mathbb{R}$ und $n \in \mathbb{Z}$

Potenzfunktionen, Potenzfunktion — Verschiedene Potenzfunktionen

Je nachdem, ob positiv oder negativ, gerade oder ungerade ist, ergeben sich verschiedene Graphen von Potenzfunktionen, die du auch im Bild siehst. Möglich sind beispielsweise Parabeln (blau lila) oder Hyperbeln (grün).

Potenzfunktionen mit positivem Exponenten

zur Stelle im Video springen

(01:24)

Eine Potenzfunktion f(x)=ax^n hat die Ordnung oder den Grad n, was der Zahl im Exponenten entspricht. Der Vorfaktor gibt an, wie steil oder flach die Funktion verläuft. Ist a<0 , so wird der Funktionsgraph zusätzlich an der x-Achse gespiegelt. Hier betrachten wir nur Potenzfunktionen mit a=1 , weil du sie so besser vergleichen kannst.

Die Funktionsgraphen verschiedener Potenzfunktionen unterscheiden sich, je nachdem ob der Exponent gerade oder ungerade ist. Für die Sonderfälle, dass n=0 oder n=1 ist, erhältst du somit eine Gerade im Koordinatensystem. Bei allen anderen Potenzfunktionen mit positivem Exponenten nennt man den Graphen dahingegen Parabel.

Ihre unterschiedlichen Formen zeigen wir dir hier:

Gerader Exponent

zur Stelle im Video springen

(01:41)

Das einfachste Beispiel einer Potenzfunktion mit geradem, positiven Exponenten kennst du bereits: Es handelt sich um die Normalparabel, ein Spezialfall der quadratischen Funktionen . Verschiedene (andere) Beispiele sind

(blau) ist die Normalparabel und eine Potenzfunktion vom Grad zwei
(lila) ist eine Parabel 4. Ordnung
$f(x)=x^{10}$ (grün) Potenzfunktion vom Grad 10

Potenzfunktionen mit positivem Exponenten, Parabeln — Potenzfunktionen mit positivem, geradem Exponenten: Parabeln

Wie du siehst, kannst du alle wichtigen Eigenschaften direkt am Funktionsgraphen ablesen:

Potenzfunktionen mit geradem, positiven Exponenten….

…sind für alle reellen Zahlen definiert, das heißt sie haben als Definitionsmenge $\mathbb{D}=\mathbb{R}$ .
… nehmen nur positive Werte an, somit ist der Wertebereich $\mathbb{W}=\mathbb{R}_0^+$ .
… sind achsensymmetrisch zu y-Achse.
…haben ihre einzige Nullstelle im Ursprung .
…verlaufen alle durch die Punkte und .
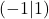…haben den Grenzwert: $\lim\limits_{x\rightarrow \infty} x^n = \infty$ und $\lim\limits_{x\rightarrow -\infty} x^n = \infty$ .
…sind streng monoton fallend für und streng monoton steigend für .

Merke: Für alle x-Werte gilt x^0 = 1 . Der Fall n=0 entspricht daher der konstanten Funktion f(x)=ax^0 = a .

Ungerader Exponent

zur Stelle im Video springen

(02:30)

Typische Beispiele für Potenzfunktionen mit positivem ungeradem Exponenten wären

(blau) lineare Funktion und Gerade
(lila) Parabel vom Grad 3
(grün) Parabel 9. Ordnung

Potenzfunktionen mit ungeradem Exponenten, Parabeln — Potenzfunktionen mit ungeradem, positivem Exponenten: Parabeln

Auch hier kannst du die wichtigsten Eigenschaften direkt am Funktionsgraphen ablesen!

Potenzfunktionen mit ungeradem, positivem Exponenten….

… sind für alle reellen Zahlen definiert, das heißt sie haben als Definitionsmenge $\mathbb{D}=\mathbb{R}$ .
… haben den Wertebereich $\mathbb{W}=\mathbb{R}$ .
… sind punktsymmetrisch zum Ursprung .
… haben ihre einzige Nullstelle im Ursprung .
… verlaufen alle durch die Punkte und .
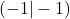… haben den Grenzwert: $\lim\limits_{x\rightarrow \infty} x^n = \infty$ und $\lim\limits_{x\rightarrow -\infty} x^n = -\infty$ .
… sind streng monoton steigend.

Merke: In beiden Fällen wird der Funktionsgraph langfristig steiler, je höher der Exponent ist und flacher für $x \in (-1|1)$ !

Merke: Falls $a\neq 1$ schneiden sich die Funktionsgraphen nicht mehr im Punkt (1|1) , die übrigen Eigenschaften gelten (mit eventuell vertauschten Vorzeichen für a<0 ) trotzdem! Genauer erklären wir das in den weiter unten stehenden Aufgaben.

Potenzfunktionen mit negativem Exponenten

zur Stelle im Video springen

(03:03)

Potenzfunktionen mit negativem Exponenten können immer als Bruch dargestellt werden, sie beschreiben eine gebrochen rationale Funktion , deren Funktionsgraph einer Hyperbel entspricht.

Funktionsgleichung einer Potenzfunktion mit negativem Exponenten

$f(x)=x^{-n} = \cfrac{1}{x^n}$

Die Funktionsgraphen unterscheiden sich auch in diesem Fall, je nachdem ob der Exponent gerade oder ungerade ist. Beide Fälle haben jedoch die x-Achse und die y-Achse als Asymptoten .

Gerader Exponent

zur Stelle im Video springen

(03:54)

Potenzfunktionen mit negativem, geradem Exponenten sind beispielsweise:

$f(x) = x^{-2}=\frac{1}{x^2}$ (blau)
$f(x) = x^{-4}=\frac{1}{x^4}$ (lila)
$f(x) = x^{-12}=\frac{1}{x^{12}}$ (grün)

Hyperbel, negativer Exponent, 1/x^2 — Potenzfunktionen mit geradem, negativen Exponenten: Hyperbel

Die wichtigsten Eigenschaften von Funktionen dieser Art kannst du abermals am Funktionsgraphen ablesen.

Potenzfunktionen mit geradem, negativen Exponenten….

… haben eine Definitionslücke bei , das heißt die Definitionsmenge ist $\mathbb{D}=\mathbb{R} \setminus \{0\}$ .
… haben den Wertebereich $\mathbb{W}=\mathbb{R}^+$ .
… sind achsensymmetrisch zur y-Achse.
… haben keine Nullstellen, stattdessen ist die x-Achse eine waagrechte Asymptote.
… haben die y-Achse als senkrechte Asymptote.
… verlaufen alle durch die Punkte und .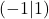
… haben die Grenzwerte: $\lim\limits_{x\rightarrow \pm \infty} x^{-n} = 0$ und $\lim\limits_{x\rightarrow \pm 0} x^{-n} = \infty$ .
… sind streng monoton steigend für und streng monoton fallend für .

Ungerader Exponent

zur Stelle im Video springen

(03:34)

Auch eine Potenzfunktion mit ungeradem negativem Exponenten hat den Funktionsgraph einer Hyperbel, wie du direkt an den folgenden Beispielen siehst:

$f(x)=x^{-1} = \frac{1}{x}$ (blau)
$f(x)=x^{-3} = \frac{1}{x^3}$ (lila)
$f(x)=x^{-1} = \frac{1}{x}$ (grün)

1/x, Potenzfunktion, ungerader Exponent — Potenzfunktionen mit ungeradem, negativem Exponenten

Potenzfunktionen mit ungeradem, negativem Exponenten….

… haben eine Definitionslücke bei , das heißt die Definitionsmenge ist $\mathbb{D}=\mathbb{R} \setminus \{0\}$ .
… haben den Wertebereich $\mathbb{W}=\mathbb{R} \setminus \{0\}$ .
… sind punktsymmetrisch zum Ursprung.
… haben keine Nullstellen. Stattdessen ist die x-Achse eine waagrechte Asymptote.
… haben die y-Achse als senkrechte Asymptote.
… verlaufen alle durch die Punkte und .
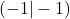… haben den Grenzwert: $\lim\limits_{x\rightarrow \pm \infty} x^n = 0$ und $\lim\limits_{x\rightarrow \pm 0} x^n = \pm\infty$ .
… sind streng monoton fallend.

Potenzfunktionen mit Bruch als Exponent

zur Stelle im Video springen

(04:11)

Es gibt auch Potenzfunktionen, deren Exponent einen Bruch enthält.

$f(x)=x^\frac{1}{n}$

Sie werden als Wurzelfunktionen bezeichnet, da du sie alternativ auch als n-te Wurzel $\sqrt[n]{}$ schreiben kannst. Typische Beispiele dafür sind

$x^\frac{1}{2}=\sqrt{x}$

$x^\frac{1}{3}=\sqrt[3]{x}$

Wurzelfunktion, Potenzfunktion rationaler Exponent — Wurzelfunktion: Potenzfunktion mit rationalem Exponenten

Ausführlich erklären wir dir das im Artikel Wurzelfunktionen .

Zusammenfassung

Fassen wir hier nochmals die wichtigsten Eigenschaften zusammen:

	positiver, gerader Exponent	positiver, ungerader Exponent	negativer, gerader Exponent	negativer, ungerader Exponent
Beispiel	$f(x)=x^4$	$f(x)=x^5$	$f(x)=x^{-2}$	$f(x)=x^{-3}$
Definitionsbereich	$\mathbb{D}=\mathbb{R}$	$\mathbb{D}=\mathbb{R}$	$\mathbb{D}=\mathbb{R} \setminus \{0\}$	$\mathbb{D}=\mathbb{R} \setminus \{0\}$
Wertebereich	$\mathbb{W}=\mathbb{R}_0^+$	$\mathbb{W}=\mathbb{R}$	$\mathbb{W}=\mathbb{R}^+$	$\mathbb{W}=\mathbb{R} \setminus \{0\}$
Nullstelle	Ursprung (0\|0)	Ursprung (0\|0)	/	/
Asymptote	/	/	x-Achse, y-Achse	x-Achse, y-Achse
Symmetrie	Achsensymmetrisch zur y-Achse	Punktsymmetrisch zum Ursprung	Achsensymmetrisch zur y-Achse	Punktsymmetrisch zum Ursprung
Monotonie	streng monoton fallend für x kleiner 0 und streng monoton steigend für x größer 0	streng monoton steigend	streng monoton steigend für x kleiner 0 und streng monoton fallend für x größer 0	streng monoton fallend
Grenzwerte	$\lim \limits_{x\rightarrow \pm \infty} x^4 = \infty$	$\lim \limits_{x\rightarrow \infty} x^5 = \infty$ $\lim \limits_{x\rightarrow -\infty} x^5 = -\infty$	$\lim \limits_{x\rightarrow \pm \infty} x^{-2} = 0$ $\lim \limits_{x\rightarrow \pm 0} x^{-2} = \infty$	$\lim \limits_{x\rightarrow \pm \infty} x^{-3}= 0$ $\lim \limits_{x\rightarrow \pm 0} x^{-3}= \pm\infty$

Potenzfunktionen Aufgaben

Im Folgenden zeigen wir dir ein paar Aufgaben mit Lösungen zum Thema Potenzfunktion.

Aufgabe 1

Bestimme die Definitions- und die Wertemenge der Funktion $f(x) = -\frac{1}{2}x^5$ und untersuche sie bezüglich Symmetrieverhalten, Monotonie, Nullstellen und Grenzwerte. Zeichne die Funktion anschließend.

Aufgabe 2

Bestimme die Definitions- und die Wertemenge der Funktion $f(x) = 3x^{-4}$ und untersuche sie bezüglich Symmetrieverhalten, Monotonie, Nullstellen und Grenzwerte. Zeichne die Funktion anschließend.

Lösungen:

Aufgabe 1

Die Funktion $f(x) = -\frac{1}{2}x^5$ ist für alle x-Werte definiert, das heißt $\mathbb{D}=\mathbb{R}$ und hat den Wertebereich $\mathbb{W}=\mathbb{R}$ . Sie ist punktsymmetrisch zum Ursprung und im ganzen Definitionsbereich streng monoton fallend. Die einzige Nullstelle befindet sich im Ursprung (0|0) . Die Grenzwerte an den Rändern des Definitionsbereichs lauten

$\lim\limits_{x\rightarrow \infty} -\frac{1}{2}x^5 = -\infty$ und $\lim\limits_{x\rightarrow -\infty} -\frac{1}{2}x^5 = \infty$

Potenzfunktionen Aufgaben, Potenzfunktionen — Aufgabe 1: Funktionsgraph

Aufgabe 2

Die Funktion $f(x) = 3x^{-4}$ hat eine Definitionslücke bei x=0 , sodass ihr Definitionsbereich $\mathbb{D}=\mathbb{R}\setminus\{0\}$ ist. Da die Potenz eine gerade Zahl ist, nimmt die Funktion nur positive Werte an, also $\mathbb{W}=\mathbb{R}^+$ . Die y-Achse ist die senkrechte Asymptote und die x-Achse die waagrechte Asymptote des Funktionsgraphen, f(x) ist achsensymmetrisch zur y-Achse. Des Weiteren ist die Funktion streng monoton steigend für x<0 und streng monoton fallend für x>0 .

Die Grenzwerte lauten

$\lim\limits_{x\rightarrow \infty} 3x^{-4} = 0$ und $\lim\limits_{x\rightarrow -\infty} 3x^{-4} = 0$

$\lim\limits_{x\rightarrow 0, x <0} 3x^{-4} = \infty$ und $\lim\limits_{x\rightarrow 0, x<0} 3x^{-4} = \infty$

Potenzfunktionen Aufgaben, Potenzfunktion — Beispiel 2: Funktionsgraph

Wurzelfunktionen

Potenzfunktionen, die einen Bruch im Exponenten haben nennt man Wurzelfunktionen. Alles was du darüber wissen musst, erfährst du in unserem Video dazu. Schau es dir unbedingt gleich an!

Funktionen

Funktionen

Zuordnungen

Funktionen

Lineare Funktionen

Funktionen

Quadratische Funktionen

Funktionen

Trigonometrische Funktionen

Funktionen

Polynome

Funktionen

Rationale Funktionen

Funktionen

Exponentialfunktion & Logarithmus

Funktionen

Fortgeschrittene trigonometrische Funktionen

Potenzfunktionen

Potenzfunktionen einfach erklärt

Potenzfunktionen mit positivem Exponenten

Gerader Exponent

Ungerader Exponent

Potenzfunktionen mit negativem Exponenten

Gerader Exponent

Ungerader Exponent

Potenzfunktionen mit Bruch als Exponent

Zusammenfassung

Potenzfunktionen Aufgaben

Aufgabe 1

Aufgabe 2

Lösungen:

Aufgabe 1

Aufgabe 2

Wurzelfunktionen

Beliebte Inhalte aus dem Bereich Funktionen

Funktionen

Funktionen Zuordnungen

Funktionen Lineare Funktionen

Funktionen Quadratische Funktionen

Funktionen Trigonometrische Funktionen

Funktionen Polynome

Funktionen Rationale Funktionen

Funktionen Exponentialfunktion & Logarithmus

Funktionen Fortgeschrittene trigonometrische Funktionen

Potenzfunktionen

Potenzfunktionen einfach erklärt

Potenzfunktionen mit positivem Exponenten

Gerader Exponent

Ungerader Exponent

Potenzfunktionen mit negativem Exponenten

Gerader Exponent

Ungerader Exponent

Potenzfunktionen mit Bruch als Exponent

Zusammenfassung

Potenzfunktionen Aufgaben

Aufgabe 1

Aufgabe 2

Lösungen:

Aufgabe 1

Aufgabe 2

Wurzelfunktionen

Beliebte Inhalte aus dem Bereich Funktionen

Funktionen

Zuordnungen

Funktionen

Lineare Funktionen

Funktionen

Quadratische Funktionen

Funktionen

Trigonometrische Funktionen

Funktionen

Polynome

Funktionen

Rationale Funktionen

Funktionen

Exponentialfunktion & Logarithmus

Funktionen

Fortgeschrittene trigonometrische Funktionen