Barwert und Endwert
In diesem Beitrag erklären wir dir, wie man jeweils den Barwert und den Endwert mithilfe von Abzinsung und Aufzinsung berechnen kann.
In unserem Video erklären wir dir die Begriffe Barwert und Endwert. Mit unserem Beispiel versteht du die Berechnung sofort!
Inhaltsübersicht
Vergleich von Zahlungsströmen: Barwert und Endwert berechnen
Das grundlegende Prinzip dabei ist, die Zahlungsströme entweder aufzuzinsen, um den Endwert berechnen zu können, oder abzuzinsen, um den Barwert berechnen zu können. Den Barwert und Endwert berechnet man deshalb, um Zahlungsströme vergleichen zu können. Dafür musst du drei Regeln beachten:
- Werte können nur zum selben Zeitpunkt verglichen oder kombiniert werden. Das heißt, wenn du die Wahl hast, entweder heute 10€ zu erhalten oder in 5 Jahren 15€, kannst du diese beiden Beträge erstmal nicht vergleichen.
- Der Zahlungsstrom lässt sich auf den Wert „heute“ berechnen. Dazu müssen zukünftige Zahlungen abgezinst, also diskontiert werden. Du kannst einen Cashflow diskontieren, indem du den Barwert berechnest. Dann siehst du, wie viel die Investition heute wert ist.
- Eine zweite Möglichkeit, dieses Problem zu umgehen, ist den Endwert zu berechnen. Indem man den Zahlungsstrom aufzinst, verschiebt man ihn quasi in die Zukunft. Das Ergebnis nennt man auch Endwert des Cashflows.
Dann schauen wir uns das Ganze im Detail an!
Barwert Definition
Einfach erklärt, sagt der Barwert aus, wie viel ein Geldbetrag in der Zukunft heute Wert ist.
Barwert berechnen
Um den Barwert zu berechnen, teile den Wert des zukünftigen Zahlungsstrom, also den Cashflow deiner Investition, durch den Diskontierungsfaktor. Der Nenner ist also der risikolose Zinssatz potenziert mit der Laufzeit der Periode, in der Regel die Anzahl der Jahre gerechnet von heute, bis du deinen Cashflow erhälst. Den Barwert berechnen kannst du einfach mit dieser Formel:
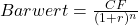
Dabei steht
- CF für den Wert zukünftiger Zahlungsströme (Cashflows)
- r für den risikolosen Zinssatz am Kapitalmarkt
- n für die Anzahl der Jahre bzw. der Laufzeit.
Mit der Formel für den Barwert lässt sich der Cashflow auf heute abzinsen , also der heutige Wert berechnen. Dabei wird der Zinseffekt eliminiert.
Beispiel zur Barwertberechnung
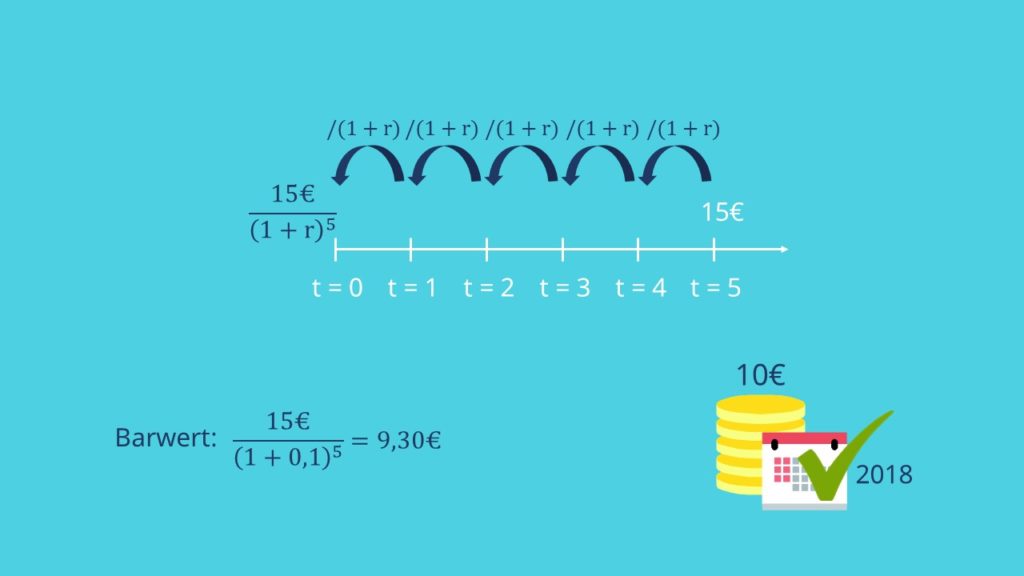
Schauen wir uns das Ganze an einem Beispiel an! Würdest du lieber 15€ in 5 Jahren erhalten oder 10 € heute? Angenommen der risikolose Zinssatz beträgt 10%. Um die beiden Zahlungsströme vergleichen zu können, kannst du den Barwert bestimmen. Dafür musst du die 15€ abzinsen. Benutzen wir hierfür unsere Formel:
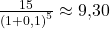
Per heute sind die 15€ also nur noch etwas mehr als 9€ wert. Nur zur Kontrolle: der exakte Barwert würde 9,31 betragen. In diesem Fall ist es also sinnvoll sich für die sofortigen 10€ zu entscheiden.
Barwertfaktor
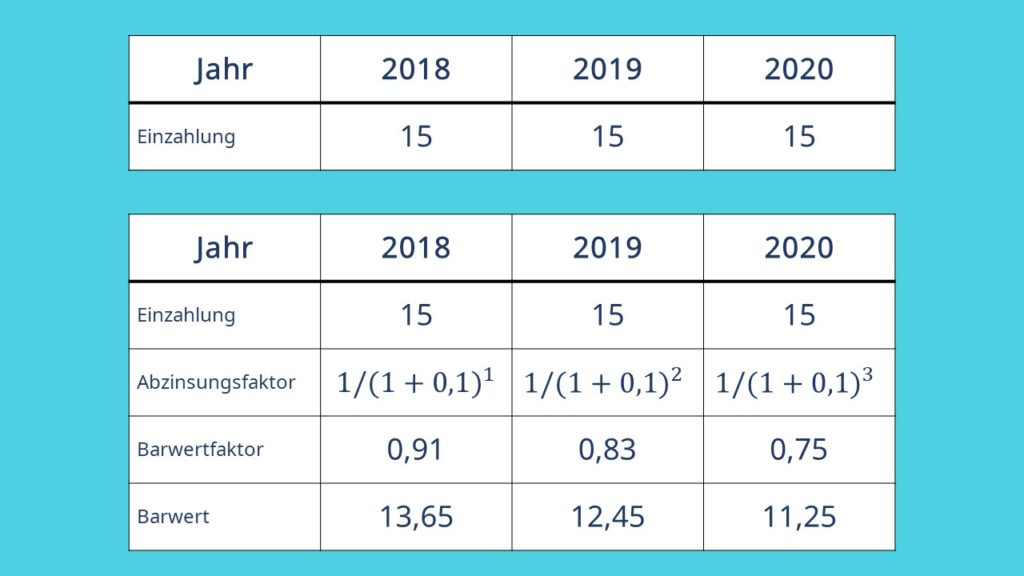
Schauen wir uns nochmal den Nenner des Bruches genauer an. 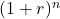 definiert als der sogenannte Diskontierungsfaktor oder auch Abzinsungsfaktor. Mit diesem lässt sich der Barwertfaktor berechnen und der entsprechende Barwert je nach Endwert und Jahr bestimmen. Um den Barwertfaktor für die einzelnen Perioden zu bestimmen, rechne den Wert des Nenners aus. Beispielsweise rechnest du in der zweiten Periode:
definiert als der sogenannte Diskontierungsfaktor oder auch Abzinsungsfaktor. Mit diesem lässt sich der Barwertfaktor berechnen und der entsprechende Barwert je nach Endwert und Jahr bestimmen. Um den Barwertfaktor für die einzelnen Perioden zu bestimmen, rechne den Wert des Nenners aus. Beispielsweise rechnest du in der zweiten Periode:
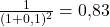
Wenn du den Barwertfaktor und den Wert des Cashflows weisst, kannst du den Barwert berechnen. Dafür nimmst du den Chasflow und multiplizierst diesen mit dem Barwertfaktor, um den Barwert zu erhalten.
Hier ist eine übersichtliche Tabelle zu unserem Beispiel.
Was der Barwert ist und wie du ihn berechnen kannst, hast du nun verstanden. Schauen wir uns als nächsten den Endwert an.
Endwert
Der Endwert wird ebenfalls verwendet, um Investitionen vergleichbar zu machen. Doch anstatt zukünftige Zahlungsströme abzuzinsen wird genau das Gegenteil gemacht: Der Wert einer Investition wird auf eine zukünftige Periode hochgerechnet.
Endwert berechnen
Du kannst einen Cashflow aufzinsen, also den Endwert berechnen, indem du ihn mit dem Faktor 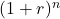 multiplizierst. Du nimmst einen heutigen Vergleichswert also den Wert der Investition heute und multiplizierst diese mit dem Aufzinsungsfaktor. Das heißt du rechnest den Wert des Cashflows mal dem risikolosen Zinssatz hoch Anzahl der Jahre für die Laufzeit. Die allgemeine Formel für die Bestimmung des Endwerts sieht also so aus:
multiplizierst. Du nimmst einen heutigen Vergleichswert also den Wert der Investition heute und multiplizierst diese mit dem Aufzinsungsfaktor. Das heißt du rechnest den Wert des Cashflows mal dem risikolosen Zinssatz hoch Anzahl der Jahre für die Laufzeit. Die allgemeine Formel für die Bestimmung des Endwerts sieht also so aus:
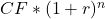
Dabei steht wieder
- CF für den Wert zukünftiger Zahlungsströme (Cashflows)
- r für den risikolosen Zinssatz am Kapitalmarkt
- n für die Anzahl der Jahre bzw. der Laufzeit.
Beispiel zur Berechnung des Endwertes
Die Formel ist gar nicht so schwer. Wenden wir das Ganze doch in der Praxis an. Halten wir uns nochmal unser Beispiel von vorhin vor Augen. Du möchtest heraus finden ob 10€ heute mehr wert sind, als 15€ in 5 Jahren. Und anstatt die 15€ abzuzinsen, rechnest du die die 10€ auf 5 Jahre hoch.
Du rechnest also einfach aus, was du in 5 Jahren erhalten würdest, wenn du die 10€ zum risikolosen Kalkulationszinssatz anlegen würdest. Um die beiden Beträge vergleichen zu können, musst du die 10 € in die Zukunft verschieben. Wenn wir wieder von einem Zinssatz in Höhe von 10% ausgehen, sähe die Rechnung also so aus:
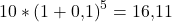
Der Endwert beträgt, wie du siehst, 16€. Jetzt weißt du, dass die 10€ heute mehr wert sind, als die 15€ in 5 Jahren!
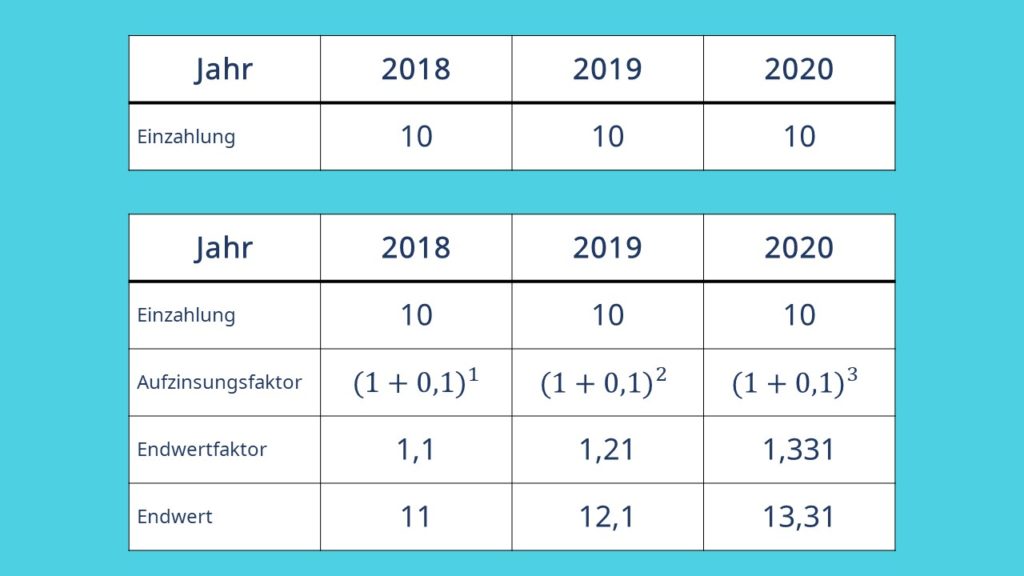
Endwertfaktor
Dabei ist 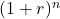 definiert als der sogenannte Aufzinsungsfaktor. Mit diesem lässt sich der Endwertfaktor berechnen und der entsprechende Endwert je nach Barwert und Jahr bestimmen. Auch hier haben wir zur Verdeutlichung eine kleine Tabelle bereitgestellt:
definiert als der sogenannte Aufzinsungsfaktor. Mit diesem lässt sich der Endwertfaktor berechnen und der entsprechende Endwert je nach Barwert und Jahr bestimmen. Auch hier haben wir zur Verdeutlichung eine kleine Tabelle bereitgestellt:
Barwertberechnung und Endwertberechnung
Du siehst: den Barwert und den Endwert zu berechnen, ist gar nicht so schwer. Zur Wiederholung siehst du hier noch einmal die beiden Formeln:
Endwert Formel: 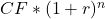
Barwert Formel: 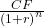
Den Barwert berechnest du also, um zukünftige Zahlungen zu einem früheren Zeitpunkt (Vergangenheit oder Gegenwart vergleichbar zu machen. Den Endwert berechnest du also, um heutige und zukünftige Investitionen vergleichen zu können.