Portfoliotheorie
Die moderne Portfoliotheorie nach Markowitz stellt ein wichtiges Konzept der Investitions- und Finanzierungsrechnung dar. Mit unserem Beitrag erklären wir dir ganz einfach, was es mit der Portfoliotheorie von Markowitz auf sich hat.
Du willst das Ganze anschaulich erklärt bekommen? Dann schau dir unser Video dazu an!
Inhaltsübersicht
Markowitz Portfolio Theory – Definition
Die Portfoliotheorie wird häufig auch als Portfolio-Selection-Theory, Markowitz Portfolio Theory oder kurz PST bezeichnet. Ziel der Portfoliotheorie von Markowitz ist die Optimierung eines Depots am Kapitalmarkt. Genauer gesagt geht es darum, deine Aktien so zu kombinieren, dass du anstatt eine Investition in Einzelaktien zu tätigen, dein Verlustrisiko durch die Bildung eines Portfolios verringerst. Für dein Portfolio selbst ist das Ziel eine möglichst hohe Rendite bei möglichst niedrigem Risiko zu erzielen.
Für die Diversifikation, also die Risikostreuung, werden der Erwartungswert, die Standardabweichung und die Korrelation der Aktien berücksichtigt. Wir gehen im Rahmen der Portfolio Theory davon aus, dass sich die empirischen Daten der vergangenen Renditen mit den zukünftigen Renditen decken.
Wenn zwei Aktien perfekt positiv korreliert sind, also eine Korrelation von eins aufweisen, entwickelt sich ihr Kurs identisch. Wenn der Kurs von Aktie A also um eine Einheit steigt, tut dies der Kurs der Aktie B ebenfalls. Für ein Portfolio wäre das natürlich ungünstig, da sich dein Ausfallrisiko dadurch nicht verringern würde.
Bei einer Korrelation von minus eins sind die beiden Aktien perfekt negativ korreliert. Dadurch heben sich die Schwankungen der beiden Kurse auf. Dein Verlustrisiko wäre also gleich null. Bei einer Korrelation von null entwickeln sich die Kurse der beiden Aktien völlig unabhängig voneinander. Durch die Risikostreuungsmöglichkeit bei einem Portfolio ist dieses immer einer Investition in eine einzelne Aktie vorzuziehen.
Portfoliotheorie Markowitz – Diversifikation eines Portfolios
Die Volatilität sinkt danach nur noch sehr gering und die Risikostreuung könnte somit bei noch mehr Aktien womöglich durch die Transaktionskosten überstiegen werden. Übrigens, das Risiko, das wir über Diversifikation eliminieren können, ist das unsystematische Risiko. Das systematische Risiko lässt sich so leider nicht beseitigen. Falls dir der Unterschied zwischen den beiden Risiken nicht ganz klar ist, solltest du unser Video dazu anschauen.
Bei der Zusammenstellung eines Portfolios ist es, wie bereits oben erwähnt, das Ziel das Risiko so zu streuen, sodass das Verhältnis von Müh und Sigma optimiert wird.
Um dir ein besseres Verständnis zu vermitteln, wie man Aktien anhand von Müh und Sigma bewerten kann, schauen wir uns dazu einen Graphen an. Auf der x-Achse wird die Volatilität und auf der y-Achse die erwartete Rendite abgebildet. Hier sind fiktive Werte für verschiedene Kursprognosen der Aktien A bis G und für einen Index I dargestellt. Wie du siehst, würde es keinen Sinn machen, die Aktie A als Einzelaktie zu wählen. Da Aktie B bei selbem Risiko eine deutlich höhere Rendite hat.
Du würdest beim Kauf von Aktie A also ein unnötiges Risiko eingehen, welches dir noch nicht einmal eine zusätzliche Rendite ermöglicht. Allerdings gibt es Aktien, die ein risikoaverser Anleger aufgrund ihrer vergangenen Kursentwicklungen einzeln zwar nie erwerben würde, diese jedoch erheblich zur Risikoreduktion im Portfolio beitragen können. Es könnte also Szenarien geben, in denen es Sinn machen würde die Aktie A für dein Portfolio auszuwählen.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Portfoliotheorie Annahmen – Vier Szenarien
Du weißt nun, was es mit der Portfoliotheorie auf sich hat. Jetzt wollen wir uns mit den vier möglichen Szenarien der Portfoliotheorie beschäftigen.
Bei der Portfoliotheorie müssen einige Annahmen berücksichtigt werden. Die Erwartungswerte und Kovarianzen müssen gegeben sein, die Wertpapiere können beliebig oft geteilt werden, die Investitionsentscheidungen basieren einzig auf Müh und Sigma, die Anleger sind risikoavers und die Investoren planen nur für eine Periode.
Außerdem können Leerverkäufe untersagt oder erlaubt sein und die Anlage zum risikofreien Zins ist entweder möglich oder nicht. Dadurch können vier Szenarien unterschieden werden. Um uns diese jeweils anzuschauen, nehmen wir wieder einen Graphen zur Hilfe. Es spielt jetzt allerdings für uns keine Rolle mehr, welche Aktie sich wo befindet, sondern wo sich in diesem Graphen Portfolios befinden.
Portfoliotheorie Annahmen – Leerverkäufe und Anlage zu risikofreiem Zins nicht möglich
Bei der ersten Möglichkeit sind Leerverkäufe und eine Anlage zum risikofreien Zins nicht möglich. Wie du in der Zeichnung sehen kannst, bestehen deine Möglichkeiten zu investieren aus einer Wolke von Portfoliomöglichkeiten. Nur die abgebildeten Portfolios sind überhaupt realisierbar. Auch für Portfolios macht es mehr Sinn, wenn sie bei weniger Risiko eine höhere Rendite abwerfen.
Du kannst übrigens sowohl für einen bestimmten Risikowert das Portfolio mit dem höchsten Erwartungswert als auch für einen bestimmten Erwartungswert das Portfolio mit dem geringsten Risiko auswählen. Es gibt also nicht nur EIN effizientes Portfolio, sondern zu JEDER Risikoeinstellung jeweils ein effizientes Portfolio. Aneinandergereiht ergeben sie die Effizienzlinie. Ganz am rechten Rand dieser Effizienzlinie findest du das Maximum-Ertrags-Portfolio MEP. Es hat den höchsten Erwartungswert, allerdings auch das größte Risiko. Am linken Rand findest du folgerichtig das Minimum-Varianz-Portfolio MVP. Also das Portfolio, das am wenigsten Risiko aufweist.
Portfoliotheorie Beispiel – Leerverkäufe nicht möglich / Anlage zu risikofreiem Zins möglich
Bei der zweiten Möglichkeit sind Leerverkäufe immer noch nicht möglich, du hast allerdings die Möglichkeit einer risikolosen Anlage. Da du hier deine Lösung nicht mehr einfach ablesen kannst, schauen wir uns das mal an einer Beispielaufgabe an. Für ein Tangentialportfolio sind die Parameter Müh gleich 15 Prozent und Sigma gleich 30 Prozent gegeben. Tangentialportfolio ist übrigens die Bezeichnung für ein universales Portfolio aus risikobehafteten Anlagen. Du möchtest 200.000 Euro investieren und der risikofreie Zins beträgt fünf Prozent. Insgesamt bist du ein recht risikofreudiger Investor und möchtest ein Risiko von 45 Prozent eingehen.
Da risikofreie Anlagen immer eine Varianz von null aufweisen, beträgt die Varianz des Portfolios hier  . Aufgelöst nach dem Gewicht des Tangentialportfolios ergibt sich der Wert 2,25. Da die beiden Gewichtungen ja zusammen immer eins ergeben müssen, ziehen wir – um die Gewichtung der risikofreien Anlage zu bestimmen – einfach
. Aufgelöst nach dem Gewicht des Tangentialportfolios ergibt sich der Wert 2,25. Da die beiden Gewichtungen ja zusammen immer eins ergeben müssen, ziehen wir – um die Gewichtung der risikofreien Anlage zu bestimmen – einfach  von
von 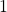 ab. Die Gewichtung der risikofreien Anlage ist also -1,25. Du nimmst somit einen Kredit über
ab. Die Gewichtung der risikofreien Anlage ist also -1,25. Du nimmst somit einen Kredit über  auf und investierst insgesamt
auf und investierst insgesamt  in dein Tangentialportfolio.
in dein Tangentialportfolio.
Unabhängig von unserem Beispiel, gibt es im Unterschied zur ersten Variante für jede Risikoeinstellung nur eine effiziente Kombination riskanter Finanztitel. Diese ist in dem Punkt, indem sich die Wolke und die Gerade der risikolosen Anlage berühren und die Steigung dieser Geraden maximal ist. Dort besteht dementsprechend das beste Verhältnis von Müh und Sigma, da die Steigung der Geraden nichts anderes abbildet als die Steigung der Rendite. Das ausgewählte Portfolio kann dann anlegerindividuell mit einer Anlage zum risikofreien Zins gemischt werden.
Portfoliotheorie – Leerverkäufe möglich / Anlage zu risikofreiem Zins nicht möglich
Bei der dritten Variante sind Leerverkäufe erlaubt. Es ist allerdings keine Anlage zum risikofreien Zins möglich. Die Kurve, die sich daraus ergibt, bildet wieder alle möglichen Müh-Sigma Kombinationen ab.
Alle Kombinationen zwischen Portfolio A und B machen keinen Sinn, da wir wieder für jeweils denselben Risikowert einen besseren Renditewert erzielen können. Alle weiteren Portfolios auf der Kurve sind je nach Risikoeinstellung für unterschiedliche Anleger jeweils effizient. Ab Punkt D sollte allerdings beachtet werden, dass für wenig Renditesteigerung ein vergleichsweise hoher Anstieg des Risikos in Kauf genommen werden muss.
Portfoliotheorie – Leerverkäufe und Anlage zu risikofreiem Zins möglich
Die vierte Variante lässt sowohl Leerverkäufe als auch die Anlage zum risikofreien Zins zu. Auch hier gibt es wieder je Risikoeinstellung nur eine effiziente Kombination riskanter Finanztitel, die wiederum im Schnittpunkt der Gerade und der Kurve liegt.
Generell kannst du dir merken, dass die Anlagemöglichkeit zum risikofreien Zins und die Möglichkeit von Leerverkäufen den Erwartungswert der Renditen erhöhen.
Jetzt kannst du dir auch schon dein eigenes Portfolio zusammenstellen. Mach dir aber vorher bewusst, ob du lieber die sichere oder die unsichere Variante wählen möchtest.