Black-Scholes-Modell
Das Black-Scholes-Modell ist eine Methode zur Bewertung von Optionen. Im Unterschied zum Binomialmodell sind zum Ausübungszeitpunkt eine unendlich große Anzahl verschiedener Werte des Underyings möglich. Im folgenden Beitrag erklären wir dir das Black Scholes Modell genauer.
Wenn du das Thema schnell verstehen und einfach erklärt bekommen willst, ist unser Video eine gute Option!
Inhaltsübersicht
Black-Scholes-Modell Beispiel und Erklärung – Annahmen des Modells
Mit Hilfe des Modells nach Black Scholes schauen wir uns an, wie wir den fairen Wert von Puts und Calls nach Black and Scholes bestimmen. Der Zweck des Modells ist, verschiedene Optionen vergleichbar zu machen. Für das Black Scholes Modell müssen ein paar Annahmen vorliegen. Zunächst muss es sich um eine europäische Option handeln und der risikolose Zinssatz muss bekannt und für Kapitalanlage und -aufnahme gleich sein.
Außerdem finden während der Laufzeit der Option keine Dividendenzahlungen statt und es können Kredite in beliebiger Höhe aufgenommen werden. Europäische Option bedeutet, dass der Optionshalter sein Optionsrecht nur zu einem bestimmten Zeitpunkt, dem Ausübungs- oder auch Fälligkeitstag, wahrnehmen kann. Bei einer amerikanischen Option kann der Optionshalter sein Recht theoretisch jederzeit während der Laufzeit ausüben.
Black Scholes Formel: Call
Schauen wir uns zuerst die Bewertung eines Calls  an. Dazu sind ein paar Variablen gegeben: Zunächst einmal der Kurswert
an. Dazu sind ein paar Variablen gegeben: Zunächst einmal der Kurswert  des Underlying. Unter Underlying versteht man das Element, also zum Beispiel eine Aktie, die mit dem Optionsschein bezogen werden kann. Dann der Basispreis
des Underlying. Unter Underlying versteht man das Element, also zum Beispiel eine Aktie, die mit dem Optionsschein bezogen werden kann. Dann der Basispreis  , auch Strike oder Ausübungskurs genannt. Also im Falle eines Calls der Preis, zu dem du die Option kaufen kannst. Zusätzlich brauchen wir die Volatilität der Renditen des Underlyings
, auch Strike oder Ausübungskurs genannt. Also im Falle eines Calls der Preis, zu dem du die Option kaufen kannst. Zusätzlich brauchen wir die Volatilität der Renditen des Underlyings  , den kontinuierlichen risikofreien Zins
, den kontinuierlichen risikofreien Zins  und die Laufzeit
und die Laufzeit  der Option in Jahren. Den Wert eines Calls bestimmen wir dann anhand dieser Formel:
der Option in Jahren. Den Wert eines Calls bestimmen wir dann anhand dieser Formel:

Der Call setzt sich dann aus  Aktien
Aktien  und beispielsweise einem Zerobond
und beispielsweise einem Zerobond 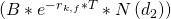 zusammen. Um den Wert des Calls berechnen zu können, müssen wir also zunächst
zusammen. Um den Wert des Calls berechnen zu können, müssen wir also zunächst  und
und  bestimmen.
bestimmen.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Black-Scholes-Modell Beispiel: Call
Schauen wir uns das mal an einem Beispiel an.  und
und  sind jeweils
sind jeweils  , die Volatilität ist gleich 35 Prozent und der kontinuierliche, risikofreie Zins ist gleich fünf Prozent. Die Laufzeit der Option beträgt ein Jahr. Während du die Formel zur Bestimmung eines Calls eventuell auswendig können musst, wird dir die Formel zur Bestimmung von
, die Volatilität ist gleich 35 Prozent und der kontinuierliche, risikofreie Zins ist gleich fünf Prozent. Die Laufzeit der Option beträgt ein Jahr. Während du die Formel zur Bestimmung eines Calls eventuell auswendig können musst, wird dir die Formel zur Bestimmung von  gegeben sein:
gegeben sein:

Wenn wir die gegebenen Werte einsetzen, bekommen wir als Ergebnis  . Diesen Wert suchen wir dann in der Verteilungsfunktion, die dir gegeben ist. Der nächstmögliche Wert bei Rundung ist dann
. Diesen Wert suchen wir dann in der Verteilungsfunktion, die dir gegeben ist. Der nächstmögliche Wert bei Rundung ist dann  . Der korrespondierende Wert in der Verteilungsfunktion der Standardnormalverteilung ist dann
. Der korrespondierende Wert in der Verteilungsfunktion der Standardnormalverteilung ist dann  .
.
Wenn du  berechnet hast, dann lässt sich
berechnet hast, dann lässt sich  ebenfalls problemlos berechnen.
ebenfalls problemlos berechnen.  und
und  stehen nämlich in folgendem Zusammenhang:
stehen nämlich in folgendem Zusammenhang:

Achte dabei allerdings darauf den genauen Wert von  und nicht den entsprechenden Wert aus der Verteilungsfunktion einzusetzen. Eingesetzt ergibt sich für
und nicht den entsprechenden Wert aus der Verteilungsfunktion einzusetzen. Eingesetzt ergibt sich für  der Wert
der Wert  . Negative Werte kannst du nicht direkt aus der Verteilungsfunktion ablesen. Du musst also
. Negative Werte kannst du nicht direkt aus der Verteilungsfunktion ablesen. Du musst also  umschreiben zu
umschreiben zu  . Jetzt suchst du in der Verteilungsfunktion der Standardnormalverteilung nach dem Wert
. Jetzt suchst du in der Verteilungsfunktion der Standardnormalverteilung nach dem Wert  . Der korrespondierende Wert ist
. Der korrespondierende Wert ist  . Diesen ziehen wir von
. Diesen ziehen wir von  ab und erhalten als Lösung für unser
ab und erhalten als Lösung für unser 
 .
.
Der Wert des Calls lässt sich dann dementsprechend durch Einsetzen der Werte von  und
und  in die Black Scholes Formel bestimmen. Der Wert deines Calls in
in die Black Scholes Formel bestimmen. Der Wert deines Calls in  beträgt also
beträgt also  Euro. Wie du siehst, musst du bei einer solchen Aufgabenstellung eigentlich nur wissen, wo du welche Werte einsetzt und wie du die Werte richtig aus der Verteilungsfunktion abliest.
Euro. Wie du siehst, musst du bei einer solchen Aufgabenstellung eigentlich nur wissen, wo du welche Werte einsetzt und wie du die Werte richtig aus der Verteilungsfunktion abliest.
Black Scholes Formel: Put
Für einen Put verhält es sich quasi genauso.  und
und  werden mit den gleichen Formeln bestimmt wie beim Call.Bei der Berechnung des Puts werden lediglich die Terme vertauscht. Jetzt werden die Aktien also vom Zerobond abgezogen.
werden mit den gleichen Formeln bestimmt wie beim Call.Bei der Berechnung des Puts werden lediglich die Terme vertauscht. Jetzt werden die Aktien also vom Zerobond abgezogen.

Generell ist bei Optionen wichtig, dass du dir immer darüber bewusst bist, dass eine Option immer ein Recht und keine Pflicht ist. Du kaufst dir als Optionshalter das Recht ein, eine Option zu ziehen oder sie verstreichen zu lassen, je nachdem wie sich der Kurs eben entwickelt. Dafür musst du dem Stillhalter, also der anderen Partei eine Prämie bezahlen. Sonst würde so ein Geschäft ja niemand eingehen wollen. Dein möglicher Verlust beschränkt sich also auf die gezahlte Prämie. Nämlich dann, wenn du die Option verstreichen lässt. Der Stillhalter hingegen kann einen Verlust machen, der theoretisch bis ins Unendliche geht. Nämlich dann, wenn er dir die Option zum Preis  verkaufen muss, der tatsächliche Wert der Option aber deutlich höher ist und immer weiter ansteigt.
verkaufen muss, der tatsächliche Wert der Option aber deutlich höher ist und immer weiter ansteigt.



