Video

Quiz

Hier geht's zum Video „Lorenzkurve“

Gini Koeffizient

Dieser Artikel behandelt den Gini Koeffizient, welcher in Prozent auch als Gini Index angegeben werden kann. Nach einer Definition und Erklärung folgt die Berechnung des Gini Koeffizient. Anhand einer Beispielaufgabe wird deutlich, wie der Gini Index berechnet und interpretiert werden kann.

Lange Definitionen und Erklärungen sind nichts für dich? In unserem Video zeigen wir dir alles was du zum Gini Index wissen musst in wenigen Minuten!

Inhaltsübersicht

Gini Koeffizient Definition

Der Gini Koeffizient oder auch Gini Index ist ein statistisches Maß zur Abbildung der relativen Konzentration von Ungleichverteilungen. Die Gini Ratio wurde vom italienischen Statistiker Corrado Gini entwickelt.

Gini Koeffizient, Gini Index, Berechnung, Definition — Gini Koeffizient

Gini Koeffizient berechnen

Aufgrund der unterschiedlichen Anwendungsbereiche gibt es viele Möglichkeiten und Formeln den Gini Koeffizienten zu bestimmen. Im Endeffekt ist das Ergebnis aber für jede Variante bis auf kleine Abweichungen aufgrund des Auf- und Abrundens dasselbe.

Gini Koeffizient Erklärung

Normalerweise nimmt der Gini Koeffizient einen Wert zwischen 0 und 1 an. Dabei bedeutet der Wert 0, dass eine totale Gleichheit der Einkommensverteilung vorliegt und die Einkommensdisparität niedrig ist. Der Wert 1 stellt folglich eine totale Ungleichheit der Einkommensverteilung dar, also eine maximale Einkommensdisparität. Der Koeffizient kann auch in Prozent angegeben werden und wird dann als Gini Index bezeichnet. Im geläufigsten Anwendungsfall wird die Einkommensverteilung der Bevölkerung eines Staates durch den Gini Koeffizienten von 0 bis 1 angegeben. Hat ein Staat einen kleinen Koeffizienten, sagt das aus, dass alle Personen ein relativ gleich hohes Einkommen haben und die Einkommensverteilung recht gleichmäßig ist.

Lorenzkurve Gini Koeffizient

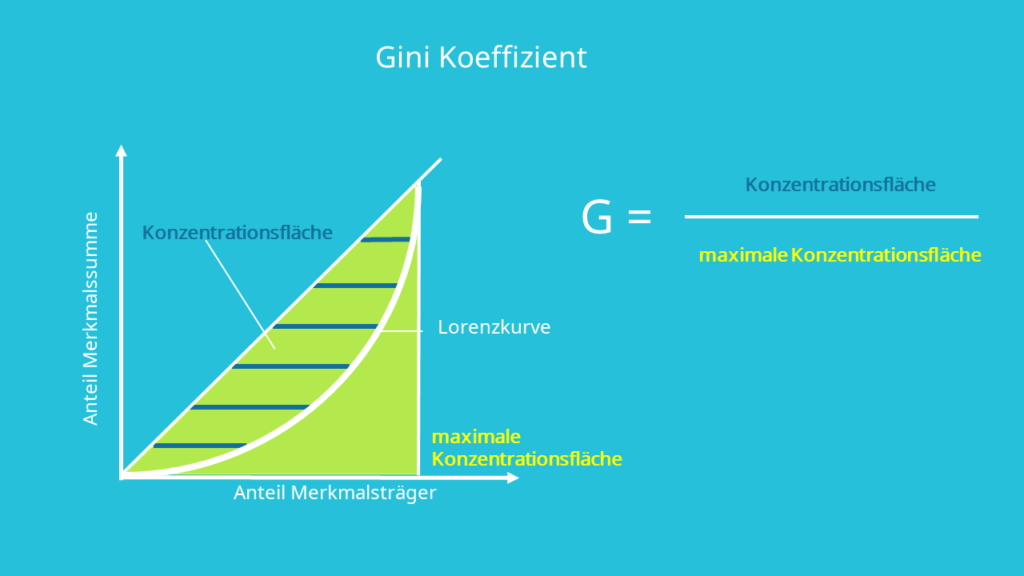
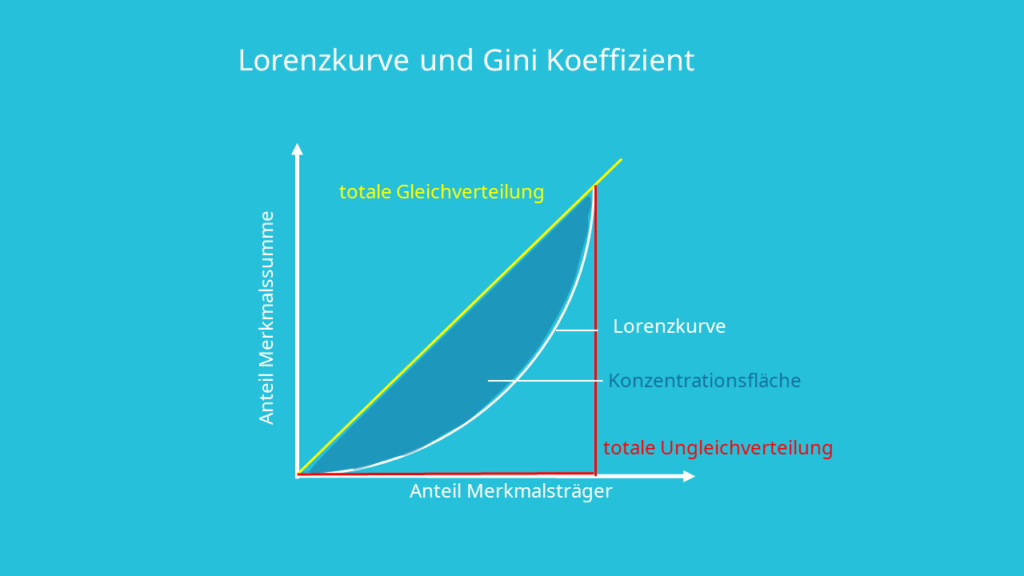
An der Lorenzkurve kann abgelesen werden, wie viel Prozent der Merkmalssumme auf wie viel Prozent der Gesamtheit der Merkmalsträger entfallen. Diese Kurve spannt sich immer zwischen den beiden Extremen der totalen Gleichheit, also der Winkelhalbierenden, und der totalen Ungleichheit auf. Der Gini Koeffizient fasst all diese Informationen in einer einzelnen Zahl zusammen und ist somit eine Maßzahl für die Ungleichheitsverteilung. Um von der Lorenzkurve den Gini Koeffizienten abzuleiten, betrachtet man die Fläche, welche sich zwischen der Lorenz- oder auch Disparitätenkurve und der Winkelhalbierenden aufspannt. Diese Fläche wird auch als Konzentrationsfläche bezeichnet. Je größer diese Fläche ist, desto größer ist logischerweise auch der Gini Koeffizient und die damit verbundene Ungleichverteilung.

Gini Koeffizient Beispielaufgabe

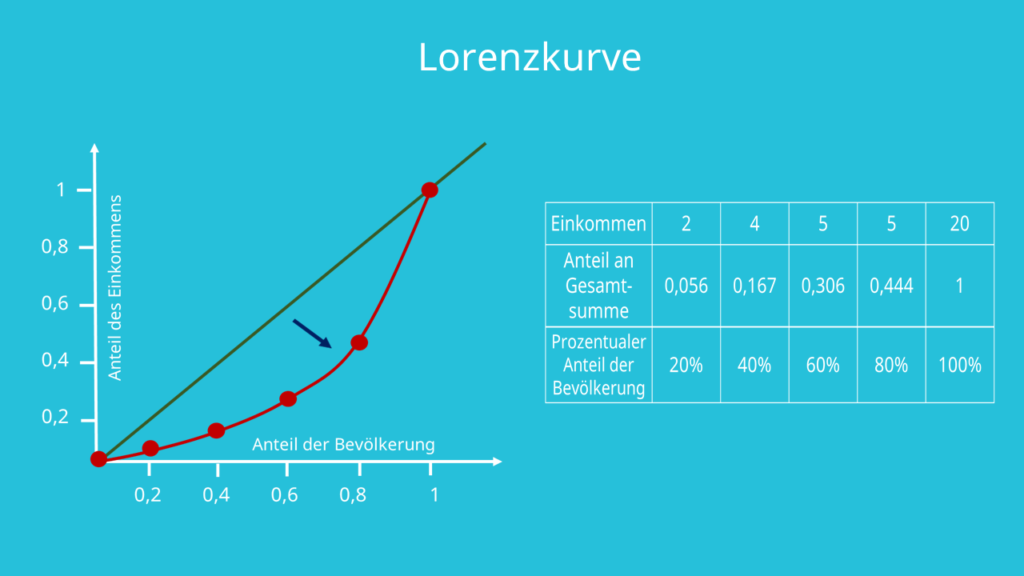
Um den Gini Koeffizienten so zu bestimmen, muss man also die Konzentrationsfläche zwischen der Winkelhalbierenden und der Lorenzkurve durch die maximal mögliche Konzentrationsfläche unter der Winkelhalbierenden teilen. Wie die Werte der Kurve berechnet werden und wie man anhand diese zeichnen kann, wird dir ausführlich im Video zur Lorenzkurve erklärt, aus welchem auch die folgenden Daten entnommen wurden:

Gini Koeffizient berechenen, Lorenzkurve, Gini Index — Beispielaufgabe Gini Koeffizient: Lorenzkurve

Das Vorgehen, um den Gini Koeffizient zu berechnen ist nun folgendes:

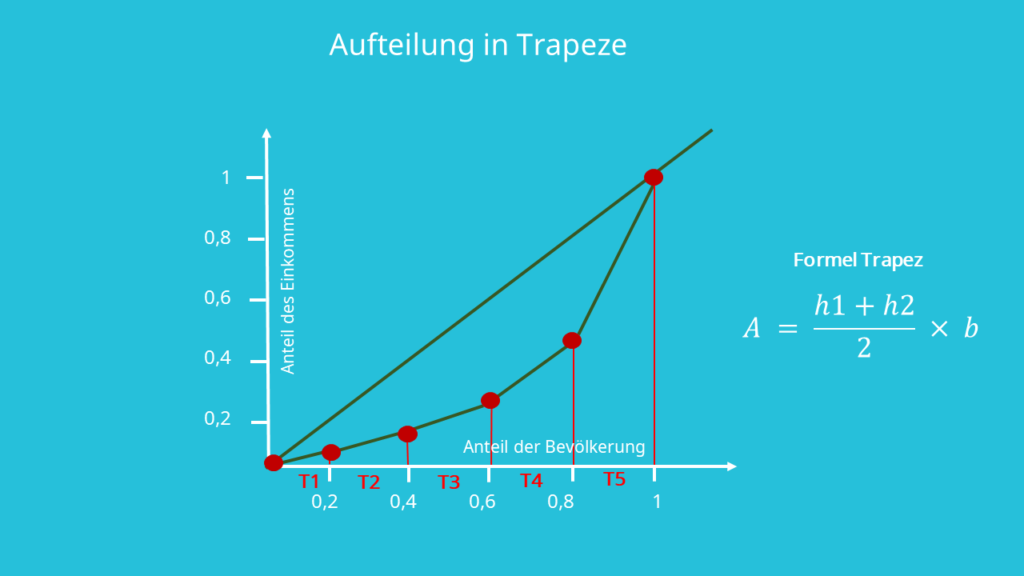
Aufteilung in einzeln zu berechnende Trapeze unter der Kurve
Subtraktion der gesamten Trapezfläche von der maximal möglichen Konzentrationsfläche ergibt die Konzentrationsfläche
Division der Konzentrationsfläche zwischen der Lorenzkurve und der Diagonalen und der möglichen Konzentrationsfläche

Aufteilung in Trapeze zur Berechnung Gini Koeffizient, Formel Trapez — Trapeze Gini Koeffizient

Die Formel zur Berechnung der Fläche eines Trapezes ist folgende:

$A\ =\ \frac{h1+h2}{2}\ \cdot\ b$

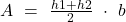
wobei h1 und h2 für die Höhe, beziehungsweise die Seitenlängen und b für die Grundfläche steht. Konkret sind die Seitenlängen die Werte, die für die entsprechenden x- Werte an der y-Achse abgetragen werden und die Grundfläche ist nichts anderes als der Anteil an der Bevölkerung, also in unserem Fall 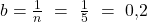$b=\frac{1}{n}\ =\ \frac{1}{5}\ =\ 0,2$ .

Für das Beispiel ergibt sich:

$T1\ =\ \frac{0+\ 0,056}{2}\ \times\ 0,2=\ 0,0056$
$T2\ =\ \frac{0,056+\ 0,167}{2}\ \cdot\ 0,2=\ 0,0223$
$T3\ =\ \frac{0,167+\ 0,306}{2}\ \cdot\ 0,2=\ 0,0473$
$T4\ =\ \frac{0,306+\ 0,444}{2}\ \cdot\ 0,2=\ 0,075$
$T5\ =\ \frac{0,444+\ 1}{2}\ \cdot\ 0,2=\ 0,1444$

$T1+T2+T3+T4+T5=\ 0,0056+0,0223+0,0473+0,075+0,1444=\ 0,2946$

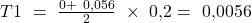
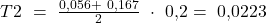
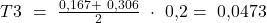
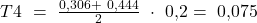
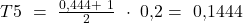
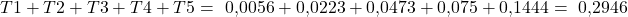
Damit wir die Konzentrationsfläche erhalten, ziehen wir die Summe der Trapezflächen von der maximal möglichen Konzentrationsfläche ab. Die maximale Konzentrationsfläche ist 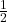$\frac{1}{2}$ , da diese genau die Fläche unter der Winkelhalbierenden entspricht. Somit erhalten wir:

$Konzentrationsfl\"ache=\frac{1}{2} - 0,2946 =0,2054$

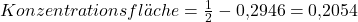
Als letzten Schritt bestimmt man den Gini Koeffizienten, indem man die errechnete Konzentrationsfläche durch die max. möglichen Konzentrationsfläche teilt.

$G=\frac{\ 0,2054\ \ }{0,5}=\ 0,41\ =\ 41\ Prozent$

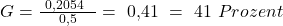
Gini Koeffizient Formel

Eine alternative Möglichkeit den Gini Koeffizienten zu bestimmen, ist die Berechnung mithilfe einer nicht ganz intuitiv herleitbaren Formel. Die kompakte Formel zur Berechnung des Gini Koeffizient ist folgende:

$G\ =\ {\frac{2\ \sum_{i=1}^{n}{ix(i)}}{n\sum_{i=i}^{n}{x(i)}}-\ \frac{n+1}{n}}$

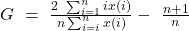
wobei x(i) das i-te Element der sortierten Daten und n die Anzahl der Personen beschreibt.
Bei den Werten von x1=2, x2=4, x3=5, x4=5, und x5=20 der 5 Personen ergibt sich also:

$2\ \sum_{i=1}^{n}{ix(i)}=2\ \cdot\ \left(1\cdot2+2\cdot4+3\cdot5+4\cdot5+5\cdot20\right)=\ 290$

$n\sum_{i=i}^{n}{x(i)}\ =\ 5\ \cdot\ \left(2+4+5+5+20\right)=180$

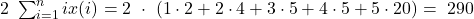
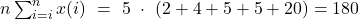
Nun müssen wir nur noch die Werte einsetzen und den Gini Index zu berechnen:

$G\ =\ {\frac{290}{180}-\ \frac{5+1}{5}}\ =\ 0,41\ =\ 41\ Prozent$

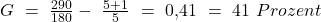
Gini Koeffizient Deutschland

Betrachtet man die Lorenzkurve und den Gini Koeffizienten der Einkommensverteilung von Deutschland wird deutlich, dass dieser für eine entwickelte Volkswirtschaft erstaunlich gering ist. Im Jahr 2016 lag der Gini Koeffizient von Deutschland bei 0.295, was bedeutet, dass das Einkommen innerhalb der Bevölkerung recht gleichmäßig verteilt ist. Die Lorenzkurve und der dazugehörige Gini Index der USA lag 2016 vergleichsweise bei 0,415. Die Mindestlohnregelung in Deutschland trägt dazu bei, dass die Lohnuntergrenze nach unten gedeckelt ist. So sollen Disparitäten eingeschränkt werden und eine möglichst gerechtere Einkommensverteilung realisiert werden.

Gini Koeffizient Interpretation

Interpretiert man den Gini Koeffizienten ist zu beachten, dass der Koeffizient nicht alle Personen einschließt, da etwa Schwarzarbeiter oder Obdachlose nicht berücksichtigt werden. Außerdem wird die unterschiedliche Verteilung innerhalb verschiedener Regionen des Landes nicht beachtet, da der Gini Koeffizient normalerweise auf nationaler Ebene bestimmt wird. Zudem bewertet der Gini Index lediglich die Verteilung, nicht aber die absolute Höhe des Einkommens in einem Land. Das heißt also, dass ein Land eine gerechte Verteilung haben kann, aber die Bevölkerung trotzdem sehr arm ist. Der Gini Koeffizient ist folglich als ein Richtwert zu sehen, welcher nur zusammen mit der Lorenzkurve wirklich aussagekräftig für die Interpretation ist, da diese nützliche Zusatzinformationen über die Verteilung liefert.

Lorenzkurve, Gini Koeffizient, Berechnung, Konzentrationsfläche — Lorenzkurve Gini Koeffizient

Gini Koeffizient Bedeutung

Grundsätzlich lässt sich ein Koeffizient für Ungleichheitsverteilungen für alle möglichen Verteilungen berechnen. Nicht nur in der Ökonomie und Informationstheorie dient der Gini Index als Maß für Ungleichheits- und Unreinheitsverteilungen. Unter anderem findet der Gini Koeffizient auch Anwendung im Bankwesen, wo er als Maß zur Trennschärfe von guten und schlechten Kunden in Ratingsystemen verwendet wird. Auch im Bereich der künstlichen Intelligenz ist der Gini Index ein effektives Hilfsmittel, um beim maschinellen Lernen und Erzeugen von Entscheidungsbäumen die richtige Entscheidungsregel auszuwählen.

Gini Koeffizient Einkommen

Vorwiegend wird der Gini Koeffizient jedoch in den Wirtschaftswissenschaften verwendet, um die Einkommens- und Vermögensverteilung einzelner Länder und den damit zusammenhängenden Entwicklungsstand zu analysieren

Funktionale Einkommensverteilung

Bei der funktionalen Einkommensverteilung wird das in der gesamten Volkswirtschaft erwirtschaftete Einkommen gemessen, welches auf die Selbstständigen und abhängig Beschäftigten aufgeteilt wird. Dazu wird eine Lohnquote und eine Gewinnquote berechnet. Manchmal berechnet man statt der Bruttolohnquote auch die Nettolohnquote.

Berechnung Bruttolohnquote, Nettolohnquote, Gewinnquote, Formel — Berechnung Bruttolohnquote Nettolohnquote Gewinnquote

Die Lohnquote ist als Kennzahl jedoch nicht ganz unproblematisch, da mittlerweile viele Menschen Zusatzeinkünfte zum Beispiel aus Geldanlagen wie Aktien beziehen. Das wird von der Lohnquote aber nicht berücksichtigt.

Daher wird für den Gini Koeffizienten nicht die funktionale, sondern die personelle Einkommensverteilung betrachtet.

Personelle Einkommensverteilung

Um die personelle Verteilung und ihre Ungleichmäßigkeit darzustellen, wird die Lorenzkurve verwendet. Schauen wir uns zur Wiederholung nochmal kurz an wie man sie erhält: Als erstes sortiert man die Haushalte nach steigendem Einkommen. An der y-Achse wird der prozentuale Anteil am Bruttoeinkommen abgetragen und auf der x-Achse werden die Haushalte nach steigendem Einkommen in Prozent sortiert. Als nächstes trägt man in das Schaubild ein, wie viel Prozent vom Gesamteinkommen die untersten n Prozent der Haushalte erhalten und erhöht schrittweise diesen Parameter n. Die Fläche zwischen der Winkelhalbierenden und der Lorenzkurve wird auch Konzentrationsfläche genannt. Je stärker diese Kurve von der Winkelhalbierenden abweicht, desto ungleicher ist die Einkommensverteilung.

Bei einer absoluten Gleichverteilung sind die Pro-Kopf-Einkommen aller verfügbaren Einkommen der Bevölkerung gleich hoch. Davon zu unterscheiden ist das Äquivalenzeinkommen, welches dem Nettoeinkommen jedes Mitglieds eines Haushalts entspricht und ihnen somit gleiche Lebensstandards ermöglicht.

Gini Koeffizient Vermögen

Betrachtet man anstelle des Einkommens das Vermögen, wird die durch den Gini-Koeffizient bestimmte Verteilung ungleicher. Aus diesem Grund lässt der Gini Koeffizient nur bedingt Rückschlüsse auf die tatsächliche Einkommensverteilung zu.

zur Videoseite: Gini Koeffizient

Beliebte Inhalte aus dem Bereich Wirtschaftspolitik

Medianwählertheorem

Dauer: 04:06

Gini Koeffizient

Medianwählertheorem

Hallo, leider nutzt du einen AdBlocker.

Auf Studyflix bieten wir dir kostenlos hochwertige Bildung an. Dies können wir nur durch die Unterstützung unserer Werbepartner tun.

Schalte bitte deinen Adblocker für Studyflix aus oder füge uns zu deinen Ausnahmen hinzu. Das tut dir nicht weh und hilft uns weiter.

Danke!
Dein Studyflix-Team

Wenn du nicht weißt, wie du deinen Adblocker deaktivierst oder Studyflix zu den Ausnahmen hinzufügst, findest du hier eine kurze Anleitung. Bitte .