Lorenzkurve
In diesem Artikel wird anschaulich erklärt, wie man die Lorenzkurve berechnet, zeichnet und was sie aussagt. Nach der Interpretation wird ein konkretes Beispiel für eine Lorenzkurve gegeben und es wird die Einkommensverteilungen auf Basis der Lorenzkurve und des Gini Koeffizienten von Deutschland betrachtet.
Das ist dir alles zu viel Text? Nach unserem Video kannst du problemlos eine Lorenzkurve berechnen, zeichnen und interpretieren, ohne dir alles durchlesen zu müssen!
Inhaltsübersicht
Lorenzkurve Definition
Die Lorenzkurve veranschaulicht die relative Konzentration der Häufigkeitsverteilung von Merkmalsträgern in Bezug zurMerkmalsumme und bildet so Ungleichheiten (Disparitäten) in beispielweiße der Einkommensverteilung graphisch ab. Umso näher die so genannte Dispatitätenkurve an der Winkelhalbierenden liegt, desto gleicher ist die Verteilung.
Lorenzkurve einfach erklärt
Die Lorenzkurve drückt folglich aus, welcher Anteil der sortierten Grundgesamtheit welchen Anteil an einer Merkmalssumme besitzt. Einfach gesagt, beschreibt die Lorenzkurve die Disparität, also die Ungleichheit, einer Verteilung. Erstmals wurde 1905 dieser Zusammenhang graphisch von dem Statistiker Max O. Lorenz dargestellt, wem die Lorenzkurve auch ihren Namen verdankt. Heutzutage wird die Lorenz- oder auch Disparitätenkurve in der Praxis daher zum Beispiel zur grafischen Veranschaulichung von Einkommensverteilungen genutzt. Die Winkelhalbierende bildet die vollkommen gerechte Gleichverteilung ab. Je weiter die Lorenzkurve von dieser Diagonalen entfernt ist, beziehungsweise je stärker die Wölbung der Kurve ist, desto ungleicher ist die Verteilung innerhalb der betrachteten Merkmalsträger.
Lorenzkurve Eigenschaften
- auf Basis empirischer Daten
- stets monoton wachsend im 1. Quadranten
- Anteile der Merkmalsträger an der Gesamtheit auf der x-Achse und Anteile an der gesamten Merkmalssumme auf der y-Achse
- verläuft konvex unterhalb der Winkelhalbierenden im Intervall [0,1]
Lorenzkurve Aussage
Was sagt die Lorenzkurve aus und was genau kann man aus der graphischen Darstellung ablesen? Jeder einzelne Punkt der Disparitätenkurve zeigt an, wie viel Prozent der Merkmalsträger welchen Anteil an der gesamten Merkmalsumme haben. So können beispielsweise Aussagen darüber getroffen werden, welchen Anteil am Gesamteinkommen das Einkommen der weniger gutverdienenden Bevölkerungsanteile ausmacht.Auf diese Weiße werden mit Hilfe der Lorenzkurve und des Gini Koeffizienten in der Praxis häufig Einkommens und Vermögensverteilungen veranschaulicht.
Lorenzkurve berechnen
Damit die Berechnung klarer ist, wird die Lorenzkurve im Folgenden anhand eines konkreten Beispiels erstellt. Dazu soll die Einkommensverteilung für einen Wirtschaftspolitik Kurs grafisch abgebildet werden. Dazu muss zuerst das Einkommen der einzelnen Personen nach der Größe aufwärts sortiert werden. Es wird davon ausgegangen, dass fünf Personen in dem Kurs sind. Der Professor verdient mit 20€ mit Abstand am meisten. Zwei Studenten haben einen Werkstudentenjob und verdienen 5€. Die anderen beiden Studenten bekommen Bafög in Höhe von 4€, beziehungsweise 2€.
Lorenzkurve Excel
Die wohl einfachste Methode eine Lorenzkurve mit komplexeren Daten zu erstellen ist es, die Werte mit Excel auszurechnen und zu visualisieren. Alles was man dazu benötigt, ist ein Datensatz und Grundkenntnisse in Excel. Bevor mit der Berechnung der Lorenzkurve mit Excel begonnen werden kann, müssen zunächst die auszuwertenden Daten in einer Tabelle abgetragen und in aufsteigender Größe sortiert werden. Danach summiert man schrittweise die Daten der Zeile, um die in der letzten Spalte die Merkmalssumme zu erhalten. Anschließend berechnet man in der darunter liegenden Zeile den relativen Anteil der einzelnen Werte an der Merkmalsumme. Dazu werden die kumulierten Einzelwerte jeweils durch die Merkmalsumme geteilt. Das Ergebnis kann nun in einer separaten Spalte in Prozent und später als y- Koordinate abgetragen werden. Die x- Koordinate berechnet man, indem man den Anteil der Merkmalträger an der Gesamtheit berechnet. Dazu werden ganz einfach die kumulierte Anzahl der Merkmalsträger eines bestimmten Merkmals durch die Gesamtzahl geteilt. Abschließend erstellt man ein Koordinatensystem und übernimmt die entsprechenden Werte für die x- und y- Achsen.
Lorenzkurve Beispiel
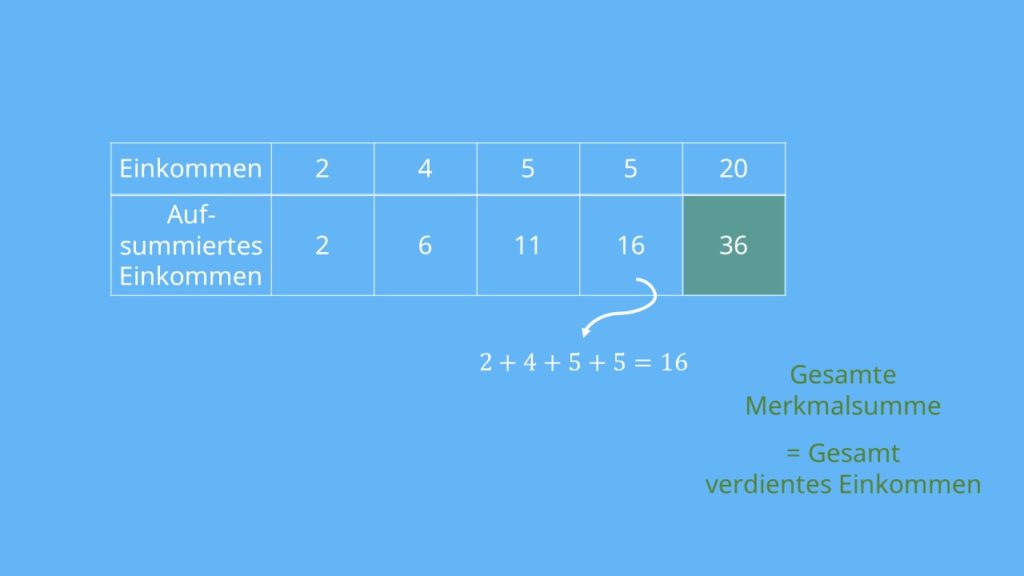
Da in der Realität enorme Datenmengen anfallen, werden zur Berechnung meist Statistikprogramme oder Excel verwendet. Die grundsätzlichen Aussagen bleiben jedoch dieselben, wenn man die Daten zum leichteren Verständnis vereinfacht. Zunächst musst du also das Einkommen Stück für Stück aufsummieren, um die Merkmalssumme zu erhalten:
Für die vierte Spalte erhältst du dann also zum Beispiel
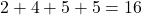
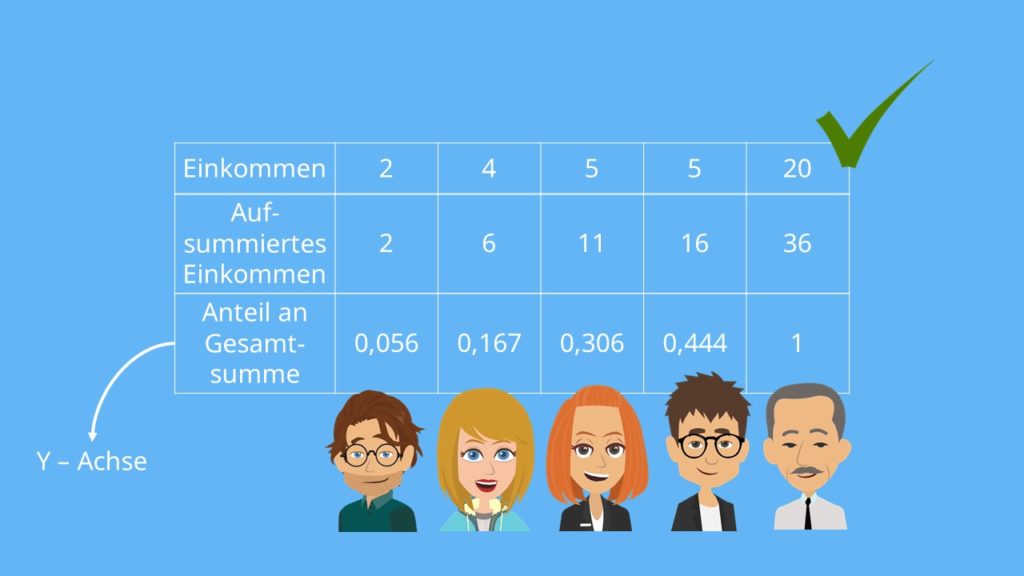
Die Merkmalsumme gibt folglich das insgesamt im Kurs verdiente Einkommen an. Als nächstes muss das aufsummierte Einkommen der Personen, also die zweite Zeile, durch das gesamte verdiente Einkommen, also 36€, geteilt werden. Für die erste Spalte rechnet man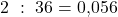 
; für die zweite 
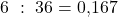und so weiter. So wird deutlich, welcher Anteil des insgesamt verdienten Einkommens jeweils auf einen Anteil der Bevölkerung entfällt.
Diesen Wert wird später an der y-Achse abgetragen, um die Lorenzkurve zu zeichnen.
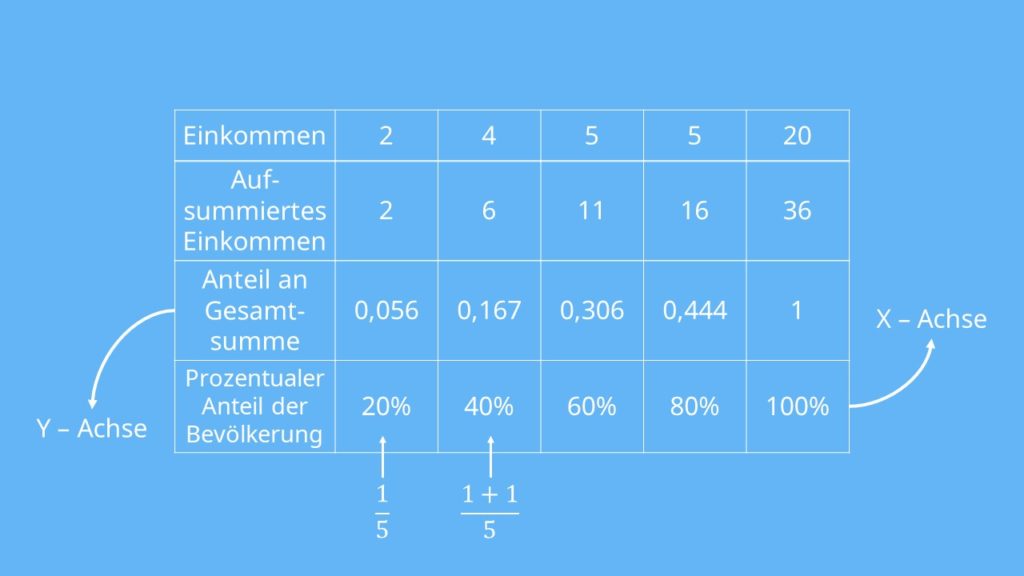
Als nächstes werden die Merkmalswerte für die x-Achse berechnet. Diese erhalten wir, indem wir die jeweiligen Bevölkerungsanteile bestimmen. Die erste Person hat einen Anteil von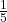 
, also 20%. Die erste plus die zweite Person haben einen Anteil von , 
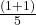, also 40% und so weiter.
Lorenzkurve zeichnen
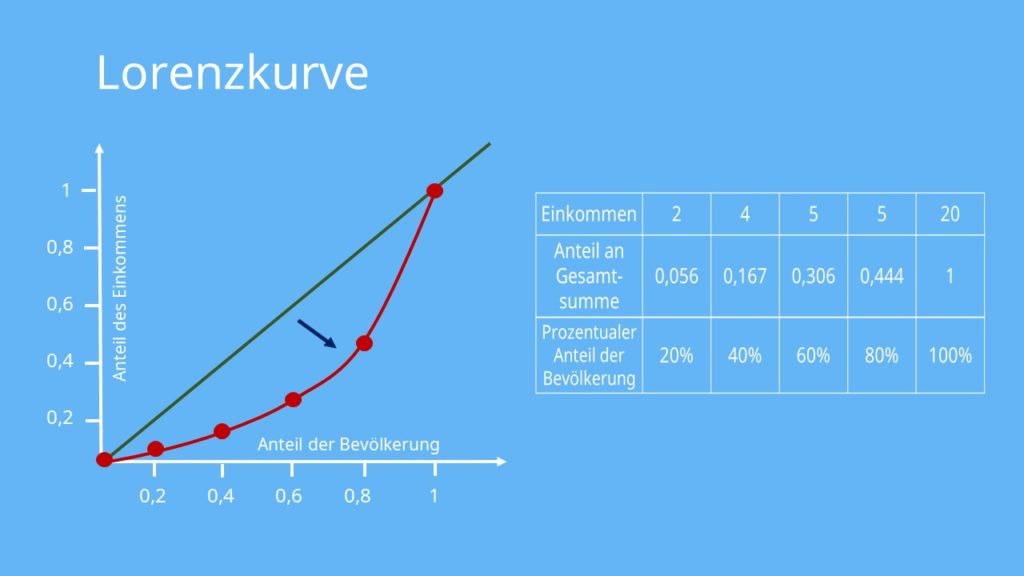
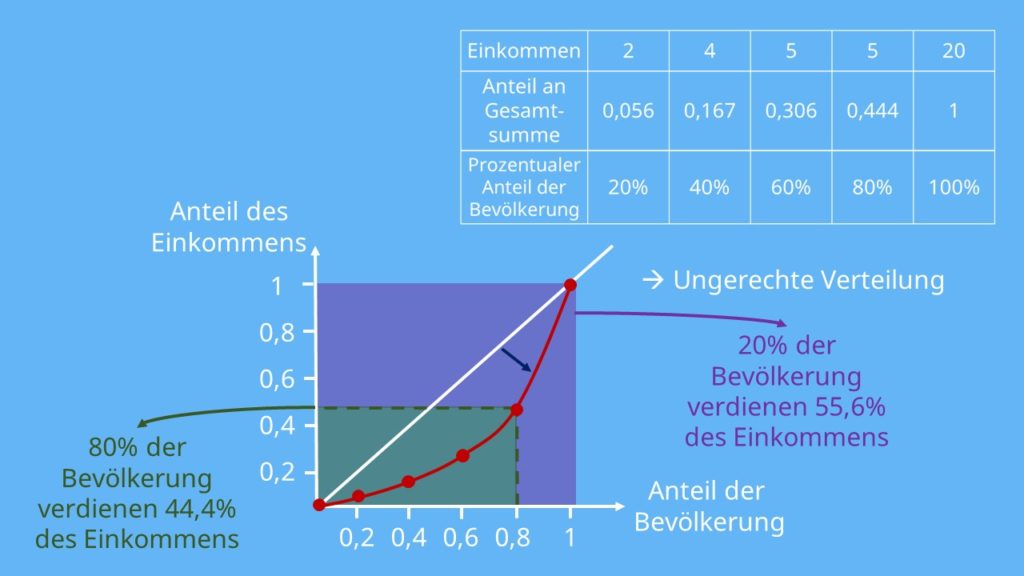
Nachdem alle Werte berechnet wurden, kann die Übertragung der berechneten Anteile in ein Koordinatensystem erfolgen. An der Ordinate wird der Anteil des Einkommens an der Gesamtsumme erfasst und an der Abszisse der Anteil an der Gesamtbevölkerung. Die Werte können einfach aus der Tabelle abgelesen und eingetragen werden.
Lorenzkurve interpretieren
Wie man anhand des so erstellten Graphen erkennen kann, ist die Einkommensverteilung dem Kurs ziemlich ungerecht. Man kann ablesen, dass die ärmeren 80% des Kurses, also die Studenten, nur 44,4% des Einkommens verdienen. Im Umkehrschluss kann man ebenso sagen, dass die reicheren 20%, also der Professor, 55,6% des Einkommens verdienen. Die Konzentration am insgesamt verdienten Einkommen ist also bei 20% der Bevölkerung höher als bei 80% der Bevölkerung.
Zur Verdeutlichung folgen zwei Beispiele, wie die Lorenzkurve aussehen würde, wenn eine Person das gesamte Einkommen verdienen würde oder wenn eine perfekte faire Gleichverteilung des Einkommens vorliegt.
Wenn du diese Punkte miteinander verbindest erhältst du die Lorenzkurve. Die Diagonale in der Abbildung zeigt quasi eine „perfekte Gleichverteilung“, also eine Lorenzkurve bei einer gerechten Einkommensverteilung. Je weiter die Lorenzkurve von dieser Diagonalen abweicht, desto ungleicher ist die Verteilung.
Beziehung zwischen Lorenzkurve und Gini Koeffizient
Der Abstand zwischen der Diagonalen und der Lorenzkurve veranschaulicht die Disparität des Einkommens der Bevölkerung und wird als Gini Koeffizient dargestellt. Dabei bedeutet der Wert 0, dass totale Gleichheit in der Einkommensverteilung herrscht und der Wert 1 totale Ungleichheit, da nur ein Individuum das gesamte Einkommen erhält.Der Gini Index hängt folglich mit der Lorenzkurve eng zusammen, da dieser die Fläche zwischen der Lorenzkurve, welche die ungleiche Verteilung abbildet, und der Winkelhalbierenden, also der Gleichverteilungsgeraden beschreibt. Häufig wird dieser auch in Prozent angegeben als Gini Index. Es kritisiert, dass er nur zusammen mit der Lorenzkurve wirklich aussagekräftig ist, da der errechnete Flächeninhalt derselbe sein kann für zwei völlig unterschiedlich verlaufende Lorenzkurven. Betrachtet man den Gini Koeffizienten und die Lorenzkurve jedoch gemeinsam, können aussagekräftige Schlussfolgerungen über gerechte beziehungsweise gleiche Verteilungen gezogen werden.
Fazit: Einkommensverteilung im Kurs
Wie du siehst, ist die Einkommensverteilung in deinem Kurs ziemlich ungerecht. Aus der Abbildung kannst du ablesen, dass die ärmeren 80% des Kurses, also deine Kommilitonen und du, nur 44,4% des Einkommens verdienen. Andersrum könnte man auch sagen, dass die reicheren 20%, also dein Professor, 55,6% des Einkommens verdienen. Die Konzentration an insgesamt verdientem Einkommen ist also bei 20% der Bevölkerung höher als bei 80% der Bevölkerung.
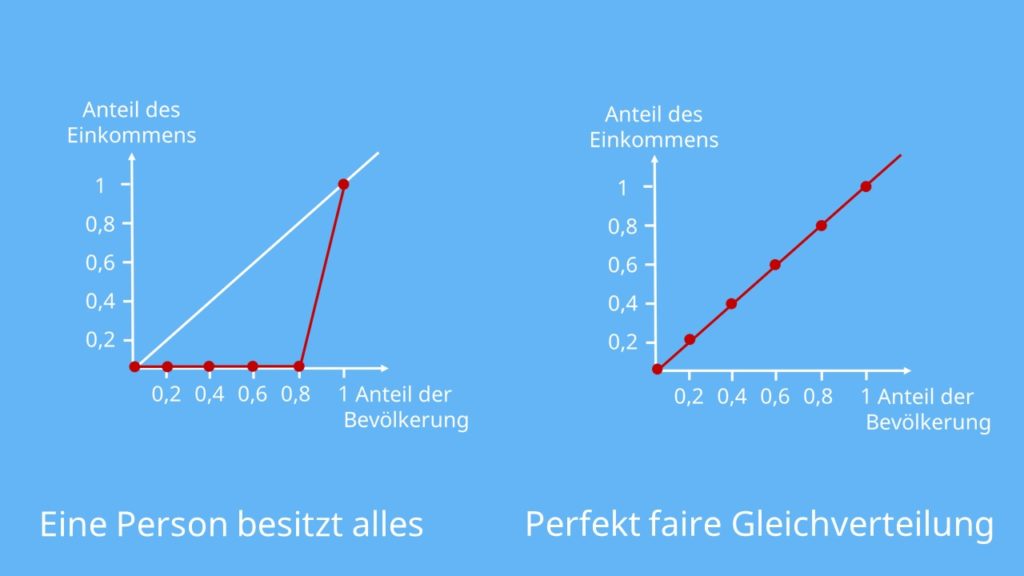
Damit es noch deutlicher wird hier noch zwei Beispiele, wie die Lorenzkurve aussehen würde, wenn eine Person das gesamte Einkommen verdienen würde oder wenn eine perfekte faire Gleichverteilung des Einkommens vorliegt.
Das eine Extrem ist eine Verteilung, bei welcher eine einzige Person alles Verdient und alle anderen nichts. Diese eine Person wäre somit für 100% der gesamten Merkmalssumme verantwortlich. Diese Lorenzkurve ist in dem folgenden Bild auf der linken Seite abgebildet und zeigt die größtmögliche Ungleichheitsverteilung. Folglich kann man sich merken; je weiter die Lorenzkurze von der Diagonalen entfernt ist, umso größer ist die Ungleichverteilung. Im anderen Extremfall, dass die gesamte Merkmalssumme gleichmäßig auf alle Merkmalsträger verteilt ist, fällt die Lorenzkurve mit der x-Achse zusammen.