Medianwählertheorem
Dieser Artikel erklärt das Medianwählertheorem nach einer Definition anschaulich anhand eines Beispiels. Dabei wird auch auf die Annahmen eingegangen, die dem Medianwählermodell zugrunde liegen. Anschließend werden die Probleme und Kritikpunkte aufgezeigt, welche bei der Anwendung in der Praxis entstehen.
Du möchtest dir das nicht alles durchlesen und das Medianwählermodell lieber schnell und einfach verstehen in kürzester Zeit? Kein Problem; sieh dir einfach unser Video an und erfahre alles was du zum Medianwählertheorem wissen musst ohne Aufwand!
Inhaltsübersicht
Medianwählertheorem Definition
Das Medianwählertheorem ist ein Modell der politischen Ökonomik, welches den Wettbewerb zwischen zwei Parteien abbildet. Die Grundaussage des Medianwählermodells ist es, dass unter der Annahme von eingipfligen Präferenzen und eindimensionalen Alternativmengen die optimale politische Position im durch den Medianwähler festgelegten Median der Präferenzen liegt.
Medianwählertheorem Annahmen
Zur Vereinfachung wird beim Medianwählermodel von einem Zweiparteiensystem ausgegangen, was zu Grunde legt, dass sowohl die Wähler als auch die Parteien Präferenzen für eine linke oder eher rechte Position auf einer Geraden haben. Zwischen den beiden extremen Positionen verändern sich die Präferenzen in gleichverteilter, kontinuierlicher Abstufung. Außerdem muss gelten, dass die Entscheidung nur eine Fragestellung betreffen darf, für welche der Wähler genau eine Alternative präferiert. Man kann die Annahmen folglich in die Hauptrkriterien des eindimensionalen Problems und der eingipfligen Präferenzen unterteilen. Die Wahl, bei der es keine Enthaltungen gibt, wird anschließend auf Basis der einfachen Mehrheitsregel entschieden, was bedeutet, dass die Partei gewinnt, welche mehr Stimmen hat.
Eindimensionales Problem
Die betrachtete Abstimmung muss über ein eindimensionales Problem erfolgen. Das heißt, dass alle Alternativen über die abgestimmt wird, auf einer Geraden gereiht werden können. Konkret wird also von einem Zweiparteiensystem ausgegangen, in welchem es nur zwei politische Parteien mit jeweils einer entgegengesetzt extremen Position gibt und die Präferenzen der Wähler sich zwischen den beiden Positionen gleichmäßig verteilen.
Eingipflige Präferenzen
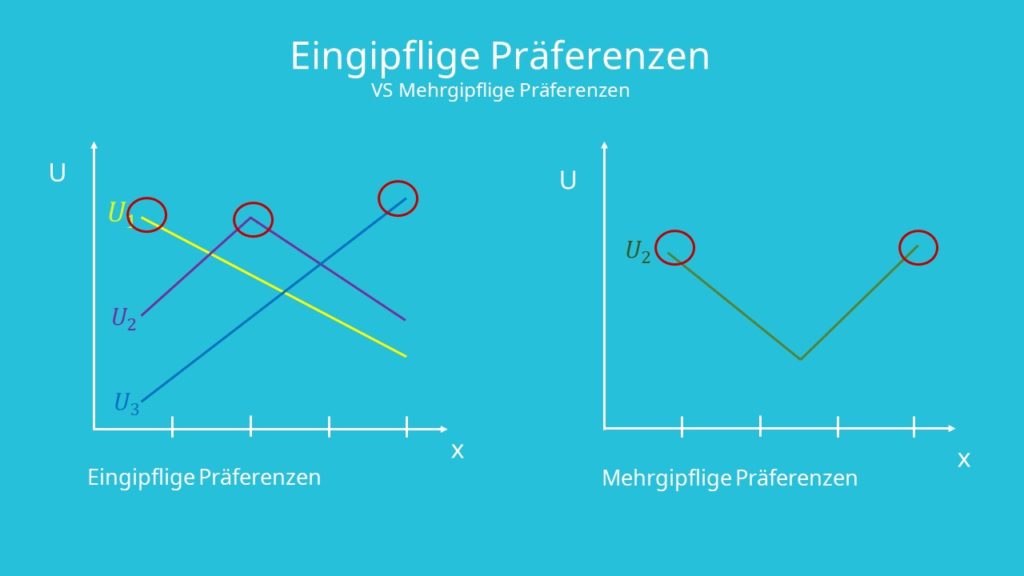
Alle Wähler müssen dabei eingipflige Präferenzen bezüglich der Alternativen haben. Das bedeutet, dass jeder Wähler genau eine optimale Alternative hat. In der linken Abbildung ist ein Beispiel für eingipflige Präferenzen zu sehen. Jeder Graph hat genau ein Maximum. In der rechten Grafik ist Beispiel für mehrgipflige Präferenzen angebildet. Hier gibt es zwei lokale Maxima. Dieser Wähler bevorzugt also extreme Positionen und hat keine eindeutige optimale Alternative.
Medianwählertheorem einfach erklärt
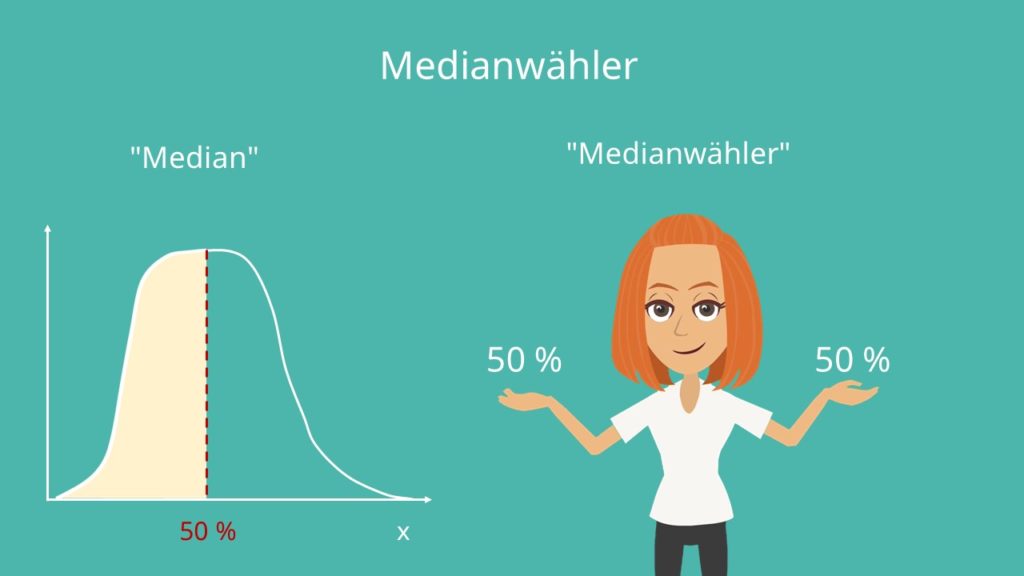
Wenn die oben genannten Annahmen erfüllt sind, wird die Mehrheit der Wähler sich für die Partei entscheiden, die den Präferenzen des Medianwählers am nächsten ist. Das Theorem besagt, dass genau eine Alternative existiert, die alle Präferenzen schlägt, und zwar der Median aller Möglichkeiten. Im Endeffekt entscheidet also die Position des Wählers der Mitte den Wahlausgang. Folglich bedeutet das, dass die beiden extremen Positionen sich immer weiter zur Mitte, also zu dem Median bewegen, um die einfache Mehrheit der Wählerstimmen zu erlangen.
Medianwählertheorem Kritik
Hauptsächlich wird an dem Medianwählermodell kritisiert, dass die zugrunde liegenden Annahmen realitätsfern sind, da in der Wirklichkeit durch Heterogenität geprägte Fragestellungen mit Überschneidungen die Regel sind und die Präferenzen weder eingipflig noch eindimensional sind. Außerdem ist es nicht realistisch eine Wahlbeteiligung von 100% zu erreichen, welche für die Gleichverteilung der Präferenzen gewährleistet sein müsste. Es ist möglich, dass Wähler, welche extreme Positionen bevorzugen, überhaupt nicht mehr wählen gehen, wenn sie sich zu wenig mit der Politik einer „Durchschnittspartei“ identifizieren können.
Medianwählertheorem Entstehung
Das Medianwählermodell hat einige Ansätze von der Hotelling-Regel übernommen. Diese Regel bietet die Grundlage für ein Modell zur Analyse der räumlichen Konkurrenz von Unternehmen. In diesem ursprünglichen Modell wird davon ausgegangen, dass zwei Konkurrenten, welche sich nur anhand ihrer Position auf einer geraden Strecken voneinander unterscheiden, sich räumlich am besten in der Mitte der Geraden positionieren sollten, um möglichst viele Kunden anzuziehen. Hotellings Modell ist auch bekannt als Eisverkäufer – Spiel, welches veranschaulicht, dass die Badegäste einer geraden Strandpromenade immer den räumlich nächsten Eisverkäufer aufsuchen. Logischerweise hat der Eisverkäufer, welcher genau in der Mitte der Strandpromenade platziert ist die meiste Kundschaft, da er die Badegäste der einen Richtung komplett für sich gewinnt und die Badegäste des Konkurrenten auf der anderen Seite zumindest teilweise. Das Medianwählermodell, wie wir es heute kennen, wurde erstmals von Ducan Blacks beschrieben im Jahr 1948 in seinem Artikel „On the Rationale of Group Decision-making“.
Medianwählertheorem Beispiel
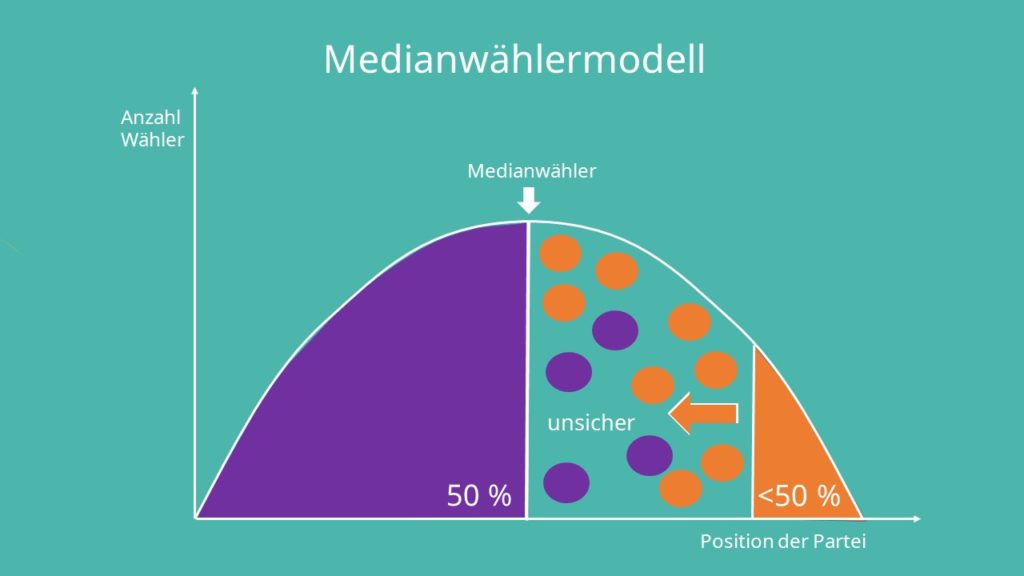
Es wird davon ausgegangen, dass der Wähler zwischen zwei Parteien entscheiden kann, nämlich der lila und der orangen Partei. Außerdem legen wir eingipflige Präferenzen und eine symmetrische Verteilung zugrunde. Es gewinnt diejenige Partei, die eine einfache Mehrheit erreicht, also mehr Stimmen als die andere Partei erzielt.
In diesem Modell würden alle Wähler links der Position der lila Partei sicher diese wählen. Alle Wähler rechts der Position der orangen Partei, würden sicher die rechte Partei wählen. Bei den Wählern, die zwischen den Positionen der beiden Parteien stehen, ist nicht sicher für welche sie sich entscheiden würden. Letztendlich gewinnt diejenige Partei, die mehr Stimmen auf sich vereinen kann. Die Partei muss sich also, um die Wahl zu gewinnen dem Median annähern.
Wenn sich die lila Partei genau auf der Position des Medianwählers positioniert, werden alle Wähler links davon, also 50%, die lila Partei wählen. Alle Wähler rechts der orangen Partei, wählen wieder diese. Das sind allerdings auf jeden Fall weniger als die lila Partei schon hat. Bei den Wählern, die zwischen den beiden Positionen stehen, ist der Ausgang nicht eindeutig. Einige werden die lila und einige die orange Partei wählen. Es ist allerdings eindeutig, dass die orange Partei nie mehr Stimmen hinter sich vereinen kann als die lila Partei, die die Position des Medianwählers vertritt. Denn wenn auch nur einer der unsicheren Wähler die lila Partei wählt, hat diese mit Sicherheit gewonnen.
Medianwählertheorem in der Praxis
Das vereinfachende Medianwählermodell kann neben dem Parteibeispiel in der Praxis auch angewendet werden, um etwa die Positionen zweier Spitzenkandidaten bei einer Präsidentschaftswahl miteinander zu vergleichen, oder um brisante Themen wie den Wahlausgang einer Direktwahl zur Einführung einer Steuer zu analysieren.
Prinzipiell kann das Modell erweitert werden, um komplexere und somit realistischere Situationen analysieren zu können. Die Analyse von Mehrparteiensystem ist beispielsweiße möglich, wenn man weitere Positionen in ein mehrdimensionales Koordinatensystem einträgt.
Das doppelte Medianwählermodell ist eine weitere denkbare Abwandlung des einfachen Modells. Beim doppelten Medianwählertheorem geht man davon aus, dass eine Partei mit einer extrem linken Position einen parteiintern sehr rechtsorientierten Spitzenkandidaten aufstellt. Dasselbe gilt im Umkehrschluss für die rechte Partei. Durch derartige Abwandlungen oder Erweiterungen des Modells versucht man die Kritikpunkte am Modell bestmöglich zu beseitigen, um das Medianwählertheorem auf wirtschaftspolitische Leben übertragen zu können und den politischen Wettbewerb bewerten zu können. Folglich kann man das Verhalten von Parteien und Politikern in politischen Systemen dennoch plausibel mit dem Medianwählermodell erklären, obwohl das Modell die Realität durch die zu Grunde liegenden Annahmen sehr vereinfacht darstellt.