Homogene & inhomogene DGL
Differentialgleichungen lassen sich in homogene und inhomogene Differentialgleichungen unterscheiden. Hier erklären wir dir, woran du diese Unterteilung formal erkennen kannst und wie sie in der Physik angewendet wird.
Inhaltsübersicht
Unterschied homogene und inhomogene Differentialgleichung
Zu Beginn schauen wir uns daher nochmal an, wie man eine Differentialgleichung allgemein schreiben kann:
Dabei sortierst du alle Ableitungen und die Funktion y selbst auf die linke Seite und alle Terme, die nur von x abhängen nach rechts. Die rechte Seite der Differentialgleichung ist die Inhomogenität. Sie wird auch Störfunktion genannt.
Homogene DGL:
Wenn b(x) = 0 ist, heißt die Differentialgleichung homogen.
Inhomogene DGL:
Ansonsten wird sie als inhomogen bezeichnet.
Inhomogenität Beispiel aus der Physik
Schauen wir uns als nächstes an, wie die Inhomogenität in der Physik vorkommt. Dafür nutzen wir das Feder-Masse-Dämpfer-System mit Federsteifigkeit k, Dämpferkonstante d und Masse m.
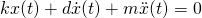
Schauen wir uns die DGL nochmals an. Hier ist unsere unbekannte Funktion die Position, die wir nach der Zeit abgeleiten. Alle x beinhaltenden Ableitungen und x selbst stehen bereits auf der linken Seite der Gleichung. Rechts steht eine Null, sodass wir folgern können, dass es sich um eine homogene Differentialgleichung handelt. Diese beschreibt nur die Eigenschwingung des Systems. Wäre die Masse zum Zeitpunkt t=0 ausgelenkt, würde sie danach wieder in den Gleichgewichtszustand schwingen und dann stillstehen.
Eine Inhomogenität wäre bei mechanischen Schwingungen eine anregende Kraft F(x)
Die inhomogene DGL beschreibt zusätzlich zur Eigenschwingung die durch die Kraft F erzwungene Schwingung. Da die Masse dauerhaft bewegt wird, pendelt sie sich nicht ein, sondern folgt der Anregung. Deshalb wird die rechte Seite auch Störfunktion genannt. Sie stört in diesem Fall die Masse daran, sich in ihrer Gleichgewichtslage einzupendeln.
Lösung der inhomogenen DGL in zwei Schritten bestimmen
Wenn du eine inhomogene Differentialgleichung vor dir hast, bestimmst du die Lösung in zwei Schritten: Du berechnest die homogene Lösung 
und die sogenannte partikuläre Lösung 
, auch spezielle Lösung der inhomogenen Gleichung genannt. Zusammen ergeben sie die Gesamtlösung
Super. Jetzt weißt du, was homogene und inhomogene Differentialgleichungen sind und hast sogar in einem Beispiel gesehen, wie du eine Inhomogenität physikalisch als anregende Kraft einer Schwingung interpretieren kannst.