Laplace Operator
Der Laplace Operator spielt in verschiedenen Gleichungen eine zentrale Rolle. Schau dir unser Video an, um das Thema in kürzester Zeit zu verstehen.
Laplace Operator einfach erklärt
Der Laplace Operator 
ist ein Differentialoperator. Wendet man ihn auf eine Funktion in kartesischen Koordinaten an, so gibt er die Summe der zweiten partiellen Ableitungen der Funktion.
Den Laplace Operator von 
kannst du folgendermaßen berechnen
.
Der Laplace Operator findet insbesondere in zwei wichtigen Gleichungen seine Anwendung: Der Laplace Gleichung und der Poisson Gleichung .
Notation: Der Laplace Operator kann auch mit dem Nabla Operator ausgedrückt werden: 
; beziehungsweise mit der Divergenz und dem Gradienten
: 
. Am Ende des Beitrags erklären wir dir diese Begriffe kurz.
Laplace Operator in kartesischen Koordinaten
In kartesischen Koordinaten lautet der Laplace Operator eines Skalarfelds 
allgemein
.
Wir beschränken uns aber auf drei Dimensionen. Hier lautet der Laplace Operator
,
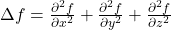wobei wir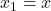 
, 
und 
gesetzt haben.
Beispiel für kartesische Koordinaten
Schauen wir uns ein konkretes Beispiel dazu an. Das folgende Skalarfeld soll gegeben sein
.
Für den Laplace Operator brauchen wir die zweiten partiellen Ableitungen nach jeder unabhängigen Variable. Dazu berechnen wir zunächst die ersten partiellen Ableitungen und erhalten
,
und
.
Daraus ergeben sich die zweiten partiellen Ableitungen
,
und
.
Diese zweiten Ableitungen müssen wir nur noch summieren. Wir bekommen als Ergebnis
.
Laplace Operator Zylinderkoordinaten
In Zylinderkoordinaten
wird jeder Punkt durch das Tripel 
lokalisiert. Damit lautet der Laplace Operator
.
Lassen wir die Höhe 
konstant, so erhalten wir den Laplace Operator in Polarkoordinaten
.
Wir haben hier 
durch 
ersetzt, da das die typische Kennzeichnung für den Abstand eines Punktes vom Ursprung in Polarkoordinaten ist.
Beispiel für Zylinderkoordinaten
Als Beispiel schauen wir uns folgendes Skalarfeld an
.
Als nächstes bestimmen wir die ersten partiellen Ableitungen nach den unabhängigen Variablen
,
und
.
Die erste Ableitung nach multiplizieren wir gemäß der Formel mit und leiten das Ergebnis erneut nach ab. Wir erhalten
.
Dieses Ergebnis teilen wir durch und bekommen den ersten Teil der Summe
.
Nun differenzieren wir noch einmal
und
.
Die zweite partielle Ableitung nach 
multiplizieren wir mit 
und bekommen für den zweiten Teil der Summe
.
Insgesamt lautet das Ergebnis
.
Laplace Operator Kugelkoordinaten
In Kugelkoordinaten
wird jeder Punkt durch das Tripel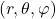 
lokalisiert. Damit lautet der Laplace Operator in Kugelkoordinaten
.
Beispiel für Kugelkoordinaten
Es sei das folgende Skalarfeld gegeben
.
Wir bestimmen zunächst die ersten partiellen Ableitungen
,
und
.
Nochmal differenziert nach ergibt Null. Damit fallen sowohl der zweite als auch dritte Teil der Summe weg.
Für den ersten Teil der Summe multiplizieren wir gemäß der Formel die erste partielle Ableitung nach mit 
und leiten das Ergebnis erneut nach ab. Wir erhalten
.
Dieses Ergebnis teilen wir durch und bekommen
.
Damit ergibt der Laplace Operator angewendet auf
.
Gradient und Divergenz
Die formale Definition des Laplace Operators beinhaltet zwei Komponenten: Den Gradienten und die Divergenz. Beides sind Differentialoperatoren.
Gradient
Haben wir ein Skalarfeld gegeben, das von 
unabhängigen Variablen 
abhängt, dann ist der Gradient von am Punkt 
folgendermaßen definiert
.
Einen ausführlichen Beitrag dazu, findest du hier .
Divergenz
Für die Divergenz schauen wir uns ein Vektorfeld in 
an. Lass uns das Vektorfeld mit 
bezeichnen. Als Abbildung nimmt ein Element aus und bildet es auf ein Element in ab. Die Divergenz von , notiert als 
, kannst du folgendermaßen berechnen
.
