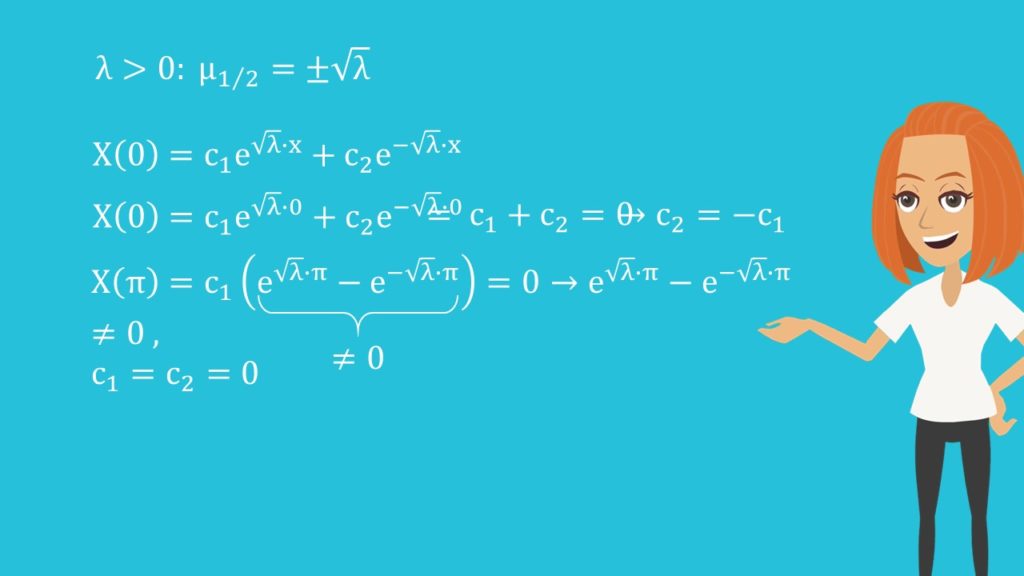Wärmeleitungsgleichung
Wie lassen sich Wärmeänderungen mathematisch abbilden? In diesem Beitrag zeigen wir dir, wie man Wärmeleitungsgleichungen mit dem Separationsansatz löst.
Inhaltsübersicht
Eindimensionale Wärmeleitungsgleichung
Die Wärmeleitungsgleichung sagt aus, wie sich die Temperatur in einem Material oder Gas über die Zeit verändert. Auch die Diffusionsgleichung wird so beschrieben. Sie gibt an, wie sich die Konzentration eines Stoffes in Raum und Zeit ändert, da der Stoff diffundiert. Die eindimensionale Wärmeleitungsgleichung, oder Diffusionsgleichung, sieht so aus. Es ist eine parabolische Differentialgleichung.

In diese setzen wir den Produktansatz

ein.

Auf der linken Seite können wir  aus der Ableitung herausziehen und auf der rechten Seite
aus der Ableitung herausziehen und auf der rechten Seite  .
.

Wir schreiben es etwas übersichtlicher,
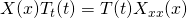
separieren die Terme

und setzen sie der Konstanten Lambda gleich.

Das machen wir, da beide Seiten nur von einer Variablen abhängen. Sie können nur gleich sein, wenn sie konstant sind.
Lösen der separierten DGL

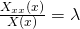
die wir getrennt voneinander lösen. Jetzt schauen wir uns die Anfangs- und Randbedingungen an.
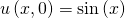
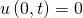
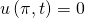
Aus diesen kannst du Anfangs- und Randbedingungen für die Funktionen T und X herleiten:



Wir beginnen mit der Lösung der von t abhängigen Gleichung.

Hier führt ein Exponentialansatz zum Ziel.

Und schon geht’s weiter mit der zweiten von x abhängigen Gleichung. Es handelt sich um eine gewöhnliche Differentialgleichung zweiter Ordnung

Hier stellen wir das charakteristische Polynom für  auf
auf

Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Sturm-Liouville-Problem
Je nachdem, welchen Wert Lambda hat, sieht die Lösung unterschiedlich aus. Es liegt ein sogenanntes Sturm-Liouville-Problem vor, das du mit Fallunterscheidung lösen kannst. Dabei musst du drei Fälle betrachten:
Der erste Fall ist, dass Lambda größer Null ist.

Dann erhältst du rein reelle Werte für Lambda.

Und deine Lösung ist eine Kombination aus zwei Exponentialfunktionen. Wir setzen die Randbedingungen ein.

 ergibt Eins, sodass die Summe
ergibt Eins, sodass die Summe  plus
plus  übrig bleibt. Also ergibt sich, dass
übrig bleibt. Also ergibt sich, dass  gleich
gleich  ist.
ist.

Lösung der zweiten Randbedingung
Die zweite Randbedingung führt auf die triviale Lösung  gleich
gleich  gleich Null, da der Ausdruck in Klammern ungleich Null ist. Der zweite Fall ist, dass
gleich Null, da der Ausdruck in Klammern ungleich Null ist. Der zweite Fall ist, dass  gleich Null ist.
gleich Null ist.

Mit der doppelten Nullstelle bei Null ergibt sich folgendes X,

in das du die Randbedingungen einsetzt.

Die erste Randbedingung ergibt, dass 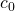 gleich Null sein muss.
gleich Null sein muss.

Die zweite Randbedingung führt auf c_Eins gleich Null. Auch hier erhalten wir also nur die triviale Lösung. Der dritte und letzte Fall ist Lambda kleiner Null.
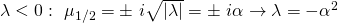
Die Eigenwerte  sind imaginäre Zahlen. Um eine bessere Übersicht zu haben, kannst du dir Alpha definieren, so dass gilt
sind imaginäre Zahlen. Um eine bessere Übersicht zu haben, kannst du dir Alpha definieren, so dass gilt

Es ergibt sich folgende Form der Lösung,

in die wir mal wieder die Randbedingungen einsetzen.

 ergibt sich zu Null.
ergibt sich zu Null.

 kann beliebig gewählt werden, solange Alpha eine natürliche Zahl n ist.
kann beliebig gewählt werden, solange Alpha eine natürliche Zahl n ist.
Hier ergibt sich endlich eine nichttriviale Lösung, sogar mehrere, da du verschiedene n einsetzen kannst. Die Gesamtlösung kannst du als Summe schreiben.
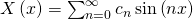
Da wir nun  kennen,
kennen,

können wir es auch in den Ansatz für T einsetzen.

Die Gesamtlösung u sieht so aus:

Jetzt setzen wir noch die Anfangsbedingung ein

Durch Koeffizientenvergleich weißt du nun, dass  und alle anderen
und alle anderen  sind.
sind.
Deine finale Lösung sieht so aus:

Achte darauf, dass in dieser kein n,  ,
,  oder C mehr vorkommt. Denn die solltest du vorher alle bestimmt haben. Jetzt weißt du, wie du die Wärmeleitungsgleichung löst und wie du mit einem Sturm-Liouville-Eigenwertproblem umgehst.
oder C mehr vorkommt. Denn die solltest du vorher alle bestimmt haben. Jetzt weißt du, wie du die Wärmeleitungsgleichung löst und wie du mit einem Sturm-Liouville-Eigenwertproblem umgehst.