Gaußsche Summenformel
Hier erklären wir dir alles, was du über die Gaußsche Summenformel wissen musst! Du möchtest dich dabei lieber entspannt zurücklehnen? Dann schau dir unser Video an!
Inhaltsübersicht
Gaußsche Summenformel einfach erklärt
Die Gaußsche Summenformel (auch kleiner Gauß) hilft dir dabei, ganz schnell die Summe beliebig vieler natürlicher Zahlen zu berechnen.

Dabei werden alle natürlichen Zahlen von 1 bis zur Grenze n addiert. Hier siehst du zum Beispiel die Summe bis n = 12.

Ohne die Gaußsche Summenformel wäre die Rechnung viel aufwendiger.

Die Gaußsche Summenformel spart dir also wirklich viel Zeit.
Gaußsche Summenformel Beispiel
Das Prinzip hinter der Gaußschen Summenformel (kleiner Gauß) ist dabei eigentlich recht einfach. Du kannst die Zahlen nämlich zu Paaren zusammenfassen. In der Tabelle zeigen wir dir das für die Zahlen von 1 bis 10, aber das funktioniert mit beliebig vielen Zahlen genauso.
| Zahlen aufwärts | Zahlen ab der Grenze abwärts | Linke Spalte + mittlere Spalte |
| 1 | 10 | 1+10=11 |
| 2 | 9 | 2+9=11 |
| 3 | 8 | 3+8=11 |
| 4 | 7 | 4+7=11 |
| 5 | 6 | 5+6=11 |
In der linken Spalte notierst du die natürlichen Zahlen aufwärts, also 1, 2, 3, … Gleichzeitig schreibst du in der mittleren Spalte die Zahlen ab deiner Grenze (dem n) rückwärts auf, in diesem Beispiel also 10, 9, 8, … Die letzte Zahl in der linken Spalte ist die 5, die letzte Zahl in der mittleren Spalte ist 6. Denn an diesem Punkt hast du alle Zahlen von 1 bis 10 einmal aufgeschrieben.
In der rechten Spalte siehst du jetzt jeweils die Summe aus der linken und mittleren Spalte, du rechnest also 1 + 10, 2 + 9, 3 + 8, … Dabei erkennst du schnell, dass diese Summe immer 11 ergibt. Statt die Zahlen von 1 bis 10 aufzuaddieren, kannst du also auch fünfmal die 11 rechnen. Es gilt


Im allgemeinen Fall sortierst du die Zahlen ebenfalls paarweise.

Auch hier hat die Summe dieser Paare immer denselben Wert, nämlich n + 1. Außerdem hast du  Paare, weil du ja die Hälfte der Zahlen in die linke Spalte der Tabelle und die andere Hälfte der Zahlen in die mittlere Spalte schreibst. So entsteht die Gaußsche Summenformel
Paare, weil du ja die Hälfte der Zahlen in die linke Spalte der Tabelle und die andere Hälfte der Zahlen in die mittlere Spalte schreibst. So entsteht die Gaußsche Summenformel
 .
.
Der berühmte Mathematiker Carl Friedrich Gauß soll die Formel angeblich schon in der Grundschule entdeckt haben. Deshalb trägt die Gaußsche Summenformel auch den Namen Kleiner Gauß. So oder so hilft dir die Formel dabei, die Summe über natürliche Zahlen schnell auszurechnen.

Bei den Zahlen von 1 bis 100 wärst du sonst sehr lange beschäftigt.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Gaußsche Summenformel Beweis
Gerade hast du schon gesehen, wie du diese Formel herleiten kannst. Es gibt aber auch einen sehr klassischen und beliebten Beweis über vollständige Induktion, der sich für die Gaußsche Summenformel anbietet.
Dabei überprüfst du zunächst, ob die Gaußsche Summenformel für eine kleine Zahl gilt. Bei diesem sogenannten Induktionsanfang setzt du n = 1 in beide Seiten der Gleichung ein.
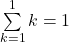

Beide Seiten liefern dasselbe Ergebnis, die Formel stimmt also für n = 1. Jetzt gehst du davon aus, dass die Gaußsche Summenformel für eine beliebige natürliche Zahl n gilt und machst den Induktionsschritt zu n+1.

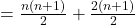



Hier formst du also einfach nur geschickt um, bis du die rechte Seite der Gleichung für n + 1 erreicht hast.
Damit hast du gezeigt, dass die Gaußsche Summenformel für alle natürlichen Zahlen  gilt.
gilt.
Du willst jetzt mehr über Induktionsbeweise erfahren? Dann schau dir gleich unser Video zur Vollständigen Induktion an! Dort erklären wir dir den Beweis zur Gaußschen Summenformel nochmal Schritt für Schritt.
