Funktionenreihen
Du hast noch Probleme mit der Aufstellung von Funktionenreihen? Wenn du dich bereits mit Funktionenfolgen auskennst, ist es garnicht mehr so schwer auch diese Thematik zu verstehen.
Inhaltsübersicht
Partialsummen aus der Funktionenfolge
Funktionenfolgen kennst du ja schon.  ist eine Funktionenfolge auf dem Intervall
ist eine Funktionenfolge auf dem Intervall  . Dann definierst du die zugehörige Funktionenreihe als Folge der Partialsummen. Das erste Folgenglied der Funktionenreihe ist also
. Dann definierst du die zugehörige Funktionenreihe als Folge der Partialsummen. Das erste Folgenglied der Funktionenreihe ist also  , das zweite ist die Partialsumme
, das zweite ist die Partialsumme  und so weiter.
und so weiter.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Bestimmung der Grenzfunktion
Ist die Funktionenfolge punktweise konvergent, kannst du die Grenzfunktion bestimmen, indem du die Summe bis unendlich laufen lässt. Diese Definition erinnert dich bestimmt stark an die punktweise Konvergenz von Funktionenfolgen. Das ist kein Zufall, denn die Funktionenreihe ist ein Spezialfall der Funktionenfolge. Daher lassen sich die Begriffe der punktweisen und gleichmäßigen Konvergenz sowie alle Eigenschaften gleichmäßig konvergenter Funktionenfolgen unmittelbar auf Funktionenreihen übertragen. Aber Achtung: Wie es auch bei einfachen Reihen geläufig ist, bezeichnet „Funktionenreihe“ oft die Grenzfunktion. Das ist nicht korrekt, aber üblich.
Funktionenreihen — häufigste Fragen
(ausklappen)
Funktionenreihen — häufigste Fragen
(ausklappen)-
Was ist der Unterschied zwischen absoluter Konvergenz und bedingter Konvergenz bei Funktionenreihen?Absolute Konvergenz einer Funktionenreihe bedeutet, dass für jedes feste
 die Zahlenreihe
die Zahlenreihe  konvergiert. Bedingte Konvergenz heißt, dass
konvergiert. Bedingte Konvergenz heißt, dass  zwar konvergiert, aber
zwar konvergiert, aber  für mindestens ein
für mindestens ein  divergiert.
divergiert.
-
Wie finde ich den Konvergenzradius bei einer Potenzreihe?Den Konvergenzradius
 der Potenzreihe
der Potenzreihe  findest du mit
findest du mit ![Rendered by QuickLaTeX.com R=\frac{1}{\limsup_{n\to\infty}\sqrt[n]{|a_n|}}](https://blog.studyflix.de/wp-content/ql-cache/quicklatex.com-18fcc64a32e6992254bcf18a09407a08_l3.png) . Existiert der Grenzwert
. Existiert der Grenzwert  , dann ist er gleich
, dann ist er gleich  . Beispiel:
. Beispiel:  ergibt
ergibt  .
.
-
Was ist der Unterschied zwischen gleichmäßiger Konvergenz und gleichmäßiger Konvergenz auf kompakten Teilmengen?Gleichmäßige Konvergenz heißt, dass
 auf dem ganzen Gebiet
auf dem ganzen Gebiet  gilt. Gleichmäßige Konvergenz auf kompakten Teilmengen bedeutet, dass diese Supremums-Bedingung für jedes kompakte
gilt. Gleichmäßige Konvergenz auf kompakten Teilmengen bedeutet, dass diese Supremums-Bedingung für jedes kompakte  gilt, aber nahe am Rand von
gilt, aber nahe am Rand von  trotzdem scheitern darf.
trotzdem scheitern darf.
-
Wie kann ich bei einer Funktionenreihe zeigen, dass die Grenzfunktion nicht stetig ist?Du zeigst, dass die Grenzfunktion nicht stetig ist, indem du eine Stelle
 findest, an der der Funktionswert-Limes nicht zum Grenzwert entlang einer Folge passt. Praktisch: Konstruiere eine Reihe mit Partialsummen
findest, an der der Funktionswert-Limes nicht zum Grenzwert entlang einer Folge passt. Praktisch: Konstruiere eine Reihe mit Partialsummen  auf
auf ![Rendered by QuickLaTeX.com [0,1]](https://blog.studyflix.de/wp-content/ql-cache/quicklatex.com-0b3fa9130fdde569e06e34d7341bf5ff_l3.png) , dann ist
, dann ist  für
für  und
und  . Weil
. Weil  aber
aber  , ist
, ist  nicht stetig.
nicht stetig.
-
Wann darf ich bei einer Funktionenreihe Grenzwert und Summenzeichen vertauschen?Grenzwert und Summenzeichen darfst du vertauschen, wenn die Funktionenreihe in einer Umgebung des Grenzübergangs gleichmäßig konvergiert und die einzelnen Grenzübergänge
 existieren. Dann gilt
existieren. Dann gilt  . Beispiel:
. Beispiel:  konvergiert gleichmäßig auf
konvergiert gleichmäßig auf ![Rendered by QuickLaTeX.com [-0{,}9,0{,}9]](https://blog.studyflix.de/wp-content/ql-cache/quicklatex.com-a0ce7094f9bafdb4e3b79c146c4627a7_l3.png) , daher darfst du bei
, daher darfst du bei  den Grenzwert gliedweise bilden.
den Grenzwert gliedweise bilden.
Eigenschaften von Funktionenreihen
Als Nächstes zeigen wir dir noch ein paar zusätzliche Eigenschaften von Funktionenreihen: Zunächst zur Konvergenz.
- Gleichmäßige Konvergenz:

Wenn du eine Zahlenfolge
 findest, mit der du die Funktionenfolge
findest, mit der du die Funktionenfolge  nach oben abschätzen kannst; das heißt eine Folge
nach oben abschätzen kannst; das heißt eine Folge  , so dass die dargestellte Ungleichung stets erfüllt ist und außerdem die Reihe zur Folge
, so dass die dargestellte Ungleichung stets erfüllt ist und außerdem die Reihe zur Folge  konvergiert,
konvergiert,
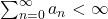
gilt folgendes: die Funktionenreihe,  konvergiert gleichmäßig.
konvergiert gleichmäßig.
- Stetigkeit:

Wenn die Funktionenreihe zur Funktionenfolge  gleichmäßig gegen
gleichmäßig gegen  konvergiert und die Funktionen
konvergiert und die Funktionen  stetig sind, dann ist auch
stetig sind, dann ist auch  stetig.
stetig.
- Vertauschung von Integral und Summation:
Wenn eine Funktionenreihe auf dem Intervall ![Rendered by QuickLaTeX.com I=\left[a,b\right]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-3ff65ba6b44f07008b722eeeb1c110d6_l3.png) gleichmäßig konvergiert und die Funktionen
gleichmäßig konvergiert und die Funktionen  integrierbar sind, dann ist auch die Grenzfunktion
integrierbar sind, dann ist auch die Grenzfunktion  integrierbar und das Integral und die Summe können vertauscht werden.
integrierbar und das Integral und die Summe können vertauscht werden.
- Vertauschung von Ableitung und Summation:
Wenn eine Funktionenreihe konvergiert und die Reihe der Ableitungen gleichmäßig konvergiert, dann ist die Grenzfunktion differenzierbar und die Differentiation und die Summe können vertauscht werden.






