Differentialgleichung
Wenn du wissen möchtest, was eine Differentialgleichung ist und was für Arten es gibt, bist du hier genau richtig! In diesem Beitrag und in unserem Video lernst du alles, was du wissen musst!
Inhaltsübersicht
Differentialgleichung einfach erklärt
Eine Differentialgleichung ist eine Gleichung aus Funktion und Ableitung(en). Du hast dann deine Funktion y(t) in Abhängigkeit ihrer Ableitung(en) angegeben. Hat deine Funktion nur eine Variable t, nennst du das eine gewöhnliche Differentialgleichung. Hier hast du ein Beispiel für eine gewöhnliche Differentialgleichung (DGL) 1. Ordnung:
y'(t) = 2 • y(t)
Wieso 1. Ordnung? Weil deine Differentialgleichung nur die erste Ableitung enthält.
Oft kennzeichnest du in Differentialgleichungen die Ableitungen auch mit Punkten (Newton-Notation) statt mit Strichen, so wie bei diesem Beispiel hier:
![\[\mathbf{\textcolor{orange}{\ddot{y}(t)}=2\textcolor{blue}{y(t)}+\textcolor{red}{\dot{y}(t)}}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-6f3ed87a86163cc4be00026797f4ee30_l3.png "Rendered by QuickLaTeX.com")
Hier stehen die zwei Punkte über dem y für die zweite Ableitung und der eine Punkt für die erste Ableitung. Es handelt sich also um eine DGL 2. Ordnung. Hast du eine Differentialgleichung höherer Ordnung gegeben, kannst du dir die allgemeine Formel merken:
![\[\mathbf{{F}}\left(t,{y}\left(t\right),{y}^\prime\left(t\right),\ldots,{y}^{\left(n\right)}\left(t\right)\right)={0}}}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-8adb93cd1dceed5da6b99c3d625637e2_l3.png "Rendered by QuickLaTeX.com")
Hier hängt deine DGL sogar von der n-ten Ableitung ab.
Wenn du eine Differentialgleichung lösen sollst, musst du eine konkrete Funktion für y(t) angeben. Wie das geht, schauen wir uns jetzt an!
Differentialgleichung erster Ordnung Beispiel
Die DGL enthält nur die Funktion y(t) und ihre erste Ableitung y'(t):
y'(t) = 2 • y(t)
An der Gleichung kannst du ablesen, dass die Ableitung genau das 2-fache der ursprünglichen Funktion ist. Oft lässt du sogar das Argument (t) weg, wenn klar ist, von was deine Funktion abhängt:
y‘ = 2 • y
Jetzt kannst du y‘ noch in der Differential-Schreibweise angeben:
![\[\textcolor{red}{\cfrac{dy}{dt}}=2\textcolor{blue}{y}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-031a53bf4112107b099b8cc9a3d87b93_l3.png "Rendered by QuickLaTeX.com")
Wenn du mit dt multiplizierst, erhältst du:
![\[dy=2y\,dt\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-555deda12995f7e095e8e1e3af3bda7f_l3.png "Rendered by QuickLaTeX.com")
Anschließend kannst du noch durch 2y teilen. So trennst du y und t voneinander (Trennung der Variablen ):
![\[\cfrac{1}{2y}\,dy=1\,dt\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-74f345aefcb353bec25320cbb55105e3_l3.png "Rendered by QuickLaTeX.com")
Zum Schluss musst du nur noch das Integral auf beiden Seiten bilden:
![\[\int{\cfrac{1}{2y}\,dy}=\int{1\,dt}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-08a5ff44acaf98baa2db4227b3e21d24_l3.png "Rendered by QuickLaTeX.com")
![\[\cfrac{1}{2} \; ln(y)=t\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-2bc78888812bdc1e27466a5710691011_l3.png "Rendered by QuickLaTeX.com")
Die Gleichung kannst du jetzt nach y auflösen:
Eine Lösung deiner DGL wäre also 
, erfüllt also deine DGL! Bei der Differentialgleichung zweiter Ordnung kannst du ähnlich vorgehen.
Differentialgleichung zweiter Ordnung Beispiel
Die DGL zweiter Ordnung hängt auch zusätzlich noch von der zweiten Ableitung ab.
![\[\textcolor{orange}{\ddot{y}(t)}=6\textcolor{blue}{y(t)}+\textcolor{red}{\dot{y}(t)}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-9614d493ba457f8c83bf668b5b059d32_l3.png "Rendered by QuickLaTeX.com")
Deine zweite Ableitung von y(t) ist also die Summe aus 6 mal y und und der ersten Ableitung von y. Hier wäre jetzt 
eine Lösung. Die erste Ableitung ist nämlich:
![\[\textcolor{red}{\dot{y}(t)}=3e^{3t}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-2b40538ba017ce0a2a13f126fef8e3f6_l3.png "Rendered by QuickLaTeX.com")
Die zweite Ableitung wäre:
![\[\textcolor{orange}{\ddot{y}(t)}=9e^{3t}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-d82351802895f3c3dc9b94d12d0aa53e_l3.png "Rendered by QuickLaTeX.com")
Setzt du die Lösung in deine Differentialgleichung ein, ergibt sich:
![\[9e^{3t}=6e^{3t}+3e^{3t}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-790e7635d727d336625cc3301ecbf30f_l3.png "Rendered by QuickLaTeX.com")
Das stimmt!
Differentialgleichung n-ter Ordnung
Natürlich kann deine DGL auch so aussehen:
Das ist dann eine Differentialgleichung n-ter Ordnung. Du benennest die Ordnung also immer nach der höchsten Ableitung! Jetzt kannst du dir noch zwei wichtige Begriffe merken:
Ist eine Differenzialgleichung nach der höchsten Ableitung aufgelöst, nennst du sie explizit:
![\[y^{(n)}=\cfrac{y+a_1y^\prime+a_2y^{\prime\prime}+\ldots+a_{n-1}y^{(n-1)}}{a_n}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-03e88d64892a738af86036c3efae0998_l3.png "Rendered by QuickLaTeX.com")
Die Beispiele, die du dir oben angeschaut hast, waren alle explizit! Ist deine Differenzialgleichung nicht nach der höchsten Ableitung aufgelöst, heißt sie implizit.
Differentialgleichungen Anwendungsbeispiel
Differentialgleichungen findest du auch oft in der Physik oder anderen Naturwissenschaften. Deshalb kann es hilfreich sein, sich auch mit Anwendungsbeispielen auseinanderzusetzen. Schau dir dafür die Differentialgleichung des freien Falls im Vakuum an. Hier betrachtest du die Beschleunigung, Geschwindigkeit und den Weg eines Gegenstandes im freien Fall.
![\[\textcolor{orange}{y''(t)}=-g \]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-2fb6b2d9c3375783d9169b992db6b24f_l3.png "Rendered by QuickLaTeX.com")
Hier steht g für die Erdbeschleunigung 9,81 m/s2. Da sich für t=0 der Gegenstand nicht bewegen soll, hast du die Nebenbedingung v(0) = y'(0)=0.
![\[\textcolor{olive}{y'(0)=0}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-7cf98bbafa167206180fddfb420d74e7_l3.png "Rendered by QuickLaTeX.com")
Um jetzt die Funktion y(t) zu finden, musst du erstmal die erste Ableitung berechnen, indem du y“(t) integrierst:
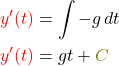
Da y'(0)=0 gilt, muss C gleich Null sein. Für deine Funktion y(t) musst du jetzt noch ein zweites Mal integrieren:
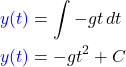
y(t) beschreibt den freien Fall im Vakuum.
Partielle Differentialgleichungen
Was ist jetzt, wenn deine Funktion von mehreren Variablen abhängt x(t, y) und du eine eine DGL lösen muss? Das nennst du dann eine partielle Differentialgleichung ! Wenn du mehr dazu wissen möchtest, schau dir doch direkt unser Video dazu an.
