Geometrische Summenformel
Du sollst die geometrische Summenformel herleiten oder beweisen? Kein Problem, wir erklären dir Schritt für Schritt wie das geht! Im Video lernst du es auf eine anschauliche Art und Weise.
Geometrische Summenformel einfach erklärt
Mit der geometrischen Summenformel kannst du Summen mit einem Exponenten schnell ausrechnen.
Dabei kannst du für q jede reelle Zahl einsetzen, außer die 1. Das n steht wie meistens für eine natürliche Zahl. Häufig brauchst du die geometrische Summenformel, um die Partialsumme einer geometrischen Reihe auszurechnen.
Satz: Geometrische Summenformel
Für alle reellen Zahlen 
und alle 
gilt
.
Beweis: Geometrische Summenformel
Nun zeigen wir dir, wie du den oberen Satz beweisen kannst.
- Schreibe zuerst die geometrische Summe aus
(I) 
- Multipliziere die gesamte Gleichung mit q, um
zu erzeugen
- Ziehe die zweite Gleichung von erster Gleichung ab
- Klammere links die Summe aus und fasse den Ausdruck rechts zusammen
- Teile die Gleichung durch
Beachte, dass du den letzten Schritt nur durchführen darfst, weil du den Fall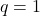 
ausgeschlossen hast. Ansonsten würdest du an dieser Stelle durch 0 teilen.
Damit hast du die geometrische Summenformel hergeleitet und der Beweis ist abgeschlossen.
Geometrische Summenformel Induktion
Du kannst die Formel aber genauso über die vollständige Induktion
beweisen. Dabei zeigst du, dass die geometrische Summenformel für alle gilt.
1.) Induktionsanfang:
Im ersten Schritt musst du zeigen, dass die Formel für 
gilt. Dafür setzt du den Wert einfach auf beiden Seiten der Gleichung ein.
Die linke und die rechte Seite der Formel liefern das gleiche Ergebnis, die Gleichung stimmt also.
2.) Induktionsschritt:
Jetzt nimmst du einmal an, dass die Formel für irgendein n gilt und gehst über zu n+1.
Induktionsvoraussetzung:
Nehme an, dass für ein beliebiges gilt.
Induktionsbehauptung:
Dann gilt für 
:
Induktionsschluss:
Hier musst du nun zeigen, dass die Gleichung aus der Induktionsbehauptung auch wirklich stimmt. Starte dafür auf der linken Seite und ziehe das letzte Glied aus der Summe heraus.
Jetzt kannst du die Induktionsvoraussetzung nutzen und musst nur noch geschickt zusammenfassen.
Damit ist der Induktionsbeweis abgeschlossen und du hast gezeigt, dass die geometrische Summenformel wirklich für alle natürlichen Zahlen gilt.
Geometrische Summenformel q=1
Die geometrische Summenformel ist nur für den Fall definiert. Der Fall 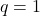ergibt sich direkt aus der Summe.
Geometrische Summe Anwendung
Die geometrische Summenformel kannst du tatsächlich in den verschiedensten Fällen anwenden. Eines der bekanntesten Beispiele ist die Verzinsung einer Rente.
Nehmen wir einmal an, dass du über 10 Jahre hinweg jedes Jahr einen Betrag von 5000€ beiseite legst und ihn zu einem Zinssatz von 2% anlegst. Dann kannst du mit Hilfe der geometrischen Summenformel ausrechnen, wie viel Geld du nach den 10 Jahren hast.
Das Geld aus dem ersten Jahr, wird für volle 10 Jahre angelegt und hat dabei einen Zuwachs von 2% Zinsen, wird also mit 1,02 multipliziert. Im nächsten Jahr profitierst du aber nur noch 9 Jahre lang von den Zinsen, dann 8 Jahre, dann 7 Jahre…
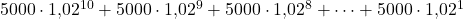
Die Rechnung kannst du jetzt zusammenfassen und mit der geometrischen Summenformel schnell ausrechnen.
Ganz ähnlich kannst du aber auch berechnen, wie dick ein Blatt Papier nach fünfmaligem Falten wird oder die Anzahl an Reiskörnern, wenn du sie jedes Jahr verdoppelst.
Geometrische Reihe
Die geometrische Summenformel brauchst du häufig, um die Partialsummen bei der geometrischen Reihe auszurechnen. Wir haben ein extra Video für dich vorbereitet, in dem du alles Wichtige über die geometrische Reihe in kurzer Zeit erfährst. Schau es dir gleich an!
