Separationsansatz
Du sitzt an einer partiellen Differentialgleichung und weißt einfach nicht, wie du sie lösen sollst? Nimm doch den Separationsansatz! Wie der funktioniert, erklären wir dir in diesem Beitrag.
Separationsansatz Beispiel
Die Differentialgleichung wird in eine örtliche und eine zeitliche Komponente separiert. Wir zeigen dir jetzt an einem Beispiel, wie du den, auch Produktansatz genannten, Separationsansatz anwendest. Eine Differentialgleichung könnte wie folgt ausschauen:

Um sie zu lösen, wählen wir einen Produktansatz.

Dafür zerlegst du u in ein Produkt aus X von x, das nur vom Ort x abhängt, und T von t, das nur von der Zeit t abhängt. Jetzt setzt du den Ansatz in die Differentialgleichung ein.

Du kannst T von t aus der partiellen Ableitung nach x herausziehen

und X von x aus der partiellen Ableitung nach t.
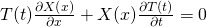
Das schreiben wir mal etwas kompakter.

Indizes zeigen hier partielle Ableitungen an. Jetzt separieren wir die ortsabhängigen Anteile und die zeitabhängigen Anteile voneinander. Daher kommt der Name Separationsansatz.
Der Ausdruck links vom Gleichheitszeichen ist nur von der Zeit t abhängig und der Ausdruck rechts vom Gleichheitszeichen nur vom Ort x. Wenn du jetzt nur die Zeit t änderst, aber an derselben Stelle x bleibst, kann sich die rechte Seite des Gleichheitszeichens nicht verändern. Folglich bleibt auch der von t abhängige Ausdruck unverändert und ist damit konstant. Es steht ja schließlich ein Gleichheitszeichen zwischen den Ausdrücken. Deshalb setzen wir die gesamte Gleichung mit einer Konstanten  gleich.
gleich.

Dadurch erhältst du zwei gewöhnliche Differentialgleichungen

Nehmen wir uns die erste vor. Wir multiplizieren die Gleichung mit groß T

und können sie jetzt zum Beispiel mit Trennung der Variablen lösen.
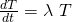
Du sortierst,

integrierst

und stellst schließlich nach  um.
um.

 ergibt sich zu
ergibt sich zu  . Analog ergibt sich für
. Analog ergibt sich für 
 .
.
Jetzt kannst du  aus den beiden Lösungen zusammensetzen.
aus den beiden Lösungen zusammensetzen.

Außerdem kannst du  und
und  zu einer Konstanten
zu einer Konstanten  zusammenfassen und auf die e-Funktionen die Potenzgesetze anwenden.
zusammenfassen und auf die e-Funktionen die Potenzgesetze anwenden.

 und Lambda kann man jetzt mithilfe von Anfangs- und Randbedingungen bestimmen. Aber du weißt ja, wie das geht. Jetzt beherrschst du den Separationsansatz. In den nächsten Beiträgen lösen wir die Wärmeleitungsgleichung, die Wellengleichung, die Laplace-Gleichung und die Poisson-Gleichung mit dem Separationsansatz.
und Lambda kann man jetzt mithilfe von Anfangs- und Randbedingungen bestimmen. Aber du weißt ja, wie das geht. Jetzt beherrschst du den Separationsansatz. In den nächsten Beiträgen lösen wir die Wärmeleitungsgleichung, die Wellengleichung, die Laplace-Gleichung und die Poisson-Gleichung mit dem Separationsansatz.

