Video

Quiz

Hier geht's zum Video „Fourierreihen“

Hier geht's zum Video „Fourier Transformation“

DFT – Diskrete Fourier-Transformation

Wichtige Inhalte in diesem Video

DFT, Fourier Transformation und Fourier Reihen

Verwandtschaft zwischen diskreter Fourier-Transformation und Fourier-Reihen

IDFT: Inverse Diskrete Fourier Transformation

Überblick Fourier Analysis

Eigenschaften der DFT

Im folgenden Artikel wird die DFT (Diskrete Fourier Transformation) erklärt und deren Verortung in der Fourier-Analysis dargelegt. Des Weiteren werden wichtige Eigenschaften der DFT gezeigt und außerdem die IDFT (Inverse DFT) erläutert.

Falls dir das zu ausführlich ausfällt, haben wir das Wichtigste zum Thema Diskrete Fourier Transformation für dich in einem anschaulichen Video zusammengefasst.

Inhaltsübersicht

DFT, Fourier Transformation und Fourier Reihen

im Videozur Stelle im Video springen

Die DFT (Diskrete Fourier Transformation) ist eine für die Praxis relevante Transformation aus dem Bereich der Fourier-Analysis.

Merke

Sie stellt eine Operation zur Bestimmung des Frequenzspektrums eines endlichen diskreten Signals dar.

Die DFT ist mit der kontinuierlichen Fourier-Transformation verwandt und lässt sich aus Überlegungen zu Fourier-Reihen ableiten.

Fourier-Transformation

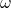Mithilfe der Fourier Transformation lassen sich nichtperiodische Funktionen $f\left(t\right)$ durch eine Linearkombination aus Sinus- und Cosinus-Funktionen verschiedener Frequenzen $\omega$ darstellen. Hierfür ordnet die Fourier-Transformierte $\hat{f}\left(\omega\right)$ jeder Frequenz $\omega\in\mathbb{R}$ diejenige Amplitude zu, mit der die Schwingung dieser Frequenz in der Linearkombination auftritt:

$\hat{f}\left(\omega\right)=\mathcal{F}\left[f\right]\left(\omega\right)\equiv\int_{-\infty}^{\ \ \infty}{\ f\left(t\right)}{\cdot e}^{-i\cdot\omega\cdot t}dt$

Die nichtperiodischen Funktionen können dann durch das Fourier-Integral – die sogenannte inverse Fourier-Transformierte – genähert werden:

${f(t)=\mathcal{F}}^{-1}\left[\hat{f}\right]\left(t\right)=\frac{1}{2\pi}\int_{-\infty}^{\ \ \infty}{\hat{f}\left(\omega\right)}{\cdot e}^{i\cdot\omega\cdot t}d\omega$

Hierbei fasst die Exponentialfunktion die Sinus- und Cosinus-Schwingungen zusammen.

Fourier-Reihen

Für periodische Funktionen f mit der Periode T sind die in der Linearkombination beteiligten Frequenzen diskret. Sie sind ein n-faches der Grundfrequenz 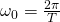$\omega_0=\frac{2\pi}{T}$ und werden mit $\omega_n$ bezeichnet. Aus dem Integral wird damit die Fourier-Reihe ,

$\mathfrak{F}[f](t)=\sum_{n=-\infty}^{\infty}c_n\cdot e^{i\cdot\omega_n\cdot t}$

wobei die Amplituden c_n das Analogon zur Fourier-Transformierten darstellen. Sie lassen sich wie folgt berechnen:

$c_n=\frac{1}{T}\int_{-T/2}^{\ \ T/2}{\ f\left(t\right)}{\cdot e}^{-i\cdot\omega_n\cdot t}dt$ ,

$k=0,\ 1,\ 2,\ldots$

Durch die Bestimmung dieser Amplituden bzw. der Fourier-Transformierten werden die betrachteten Funktionen in ihr sogenanntes Frequenzspektrum zerlegt.

Definition: Diskrete Fourier Transformierte

Mithilfe der Fourier-Transformation und der Fourier-Reihe lassen sich also die Frequenzspektren von nichtperiodischen und periodischen Funktionen ermitteln. In der Praxis liegen die zu untersuchenden Signalen allerdings nicht als Funktion vor, sondern als Menge diskreter Werte. Die Diskrete Fourier Transformation befasst sich mit der Spektralanalyse solcher diskreten endlichen Signale, welche zur Untersuchung periodisch fortgesetzt werden.

Untersucht werden sollen die $N\in\mathbb{N}$ komplexen Werte $a_0, a_1, \ldots, a_{N-1}$ , die die Signalwerte darstellen und in einem Vektor $\left(a_0,a_1,\ldots,a_{N-1}\right)=:a\in\mathbb{C}^N$ zusammengefasst werden können.

Die Diskrete Fourier Transformierte $\hat{a}=\left({\hat{a}}_0,{\hat{a}}_1,\ldots,{\hat{a}}_{N-1}\right)$ des Vektors $a\in\mathbb{C}^N$ besitzt die Koeffizienten

${\hat{a}}_n=\frac{1}{N}\sum_{k=0}^{N-1}{e^{-2\pi i\cdot\frac{k\cdot n}{N}}\cdot a_k}$

Zur Effizienten Berechnung der Diskreten Fourier Transformation gibt die FFT (Fast Fourier Transformation) einen Algorithmus an.

Verwandtschaft zwischen diskreter Fourier-Transformation und Fourier-Reihen

im Videozur Stelle im Video springen

Die DFT ist eng verwandt mit der Theorie der Fourier-Reihen bzw. sie lässt sich aus dieser ableiten. Dazu werden die einzelnen Werte a_0 , $\ldots$ , $\ a_{N-1}$ des zu untersuchenden diskreten und endlichen Signals $\left(a_0,a_1,\ldots,a_{N-1}\right)=:a\in\mathbb{C}^N$ als äquidistante Funktionswerte einer $\mathbit{T}$ -periodischen Funktion f(t) angesehen:

$a_k=f\left(k\cdot\frac{T}{N}\right)$ mit $k=0,1,\ldots,N-1$

Für eine solche $\mathbit{T}$ -periodischen Funktion f lässt sich eine Fourier-Reihe entwickeln und die Fourier-Koeffizienten lassen sich wie bereits erwähnt durch folgendes Integral berechnen:

$c_n=\frac{1}{T}\int_{-T/2}^{\ \ T/2}{\ f\left(t\right)}{\cdot e}^{-i\cdot\omega_n\cdot t}dt$ ,

$n=0,\ 1,\ 2,\ldots$

Dabei können die Grenzen des Integrals auch verschoben werden. Wichtig ist nur, dass über eine komplette Periodendauer integriert wird. Die Koeffizienten können also auch folgendermaßen berechnet werden:

$c_n=\frac{1}{T}\int_{0}^{T}{\ f\left(t\right)}{\cdot e}^{-i\cdot\omega_n\cdot t}dt$ ,

$n=0,\ 1,\ 2,\ldots$

Hierbei sind die Frequenzen $\omega_n$ ein Vielfaches der Grundfrequenz:

$\omega_n=n\cdot\frac{2\pi}{T}$

Im Fall der DFT sind allerdings nicht alle kontinuierlichen Funktionswerte bekannt, sondern nur die diskreten Messwerte $a_0,a_1,\ldots,a_{N-1}$ . Das bedeutet, dass sich dieses Integral nicht berechnen lässt. Daher wird das Integral durch eine Riemann-Summe genähert: Die Funktion ${f\left(t\right)\cdot e}^{-i\cdot\omega_n\cdot t}$ wird an den Stützstellen $t=k\cdot\frac{T}{N}$ ausgewertet, mit der Differenz zwischen zwei Stützstellen $\trianglet=\frac{T}{N}$ multipliziert und dieses Produkt wird über den Laufindex k aufsummiert. Es ergibt sich die folgende Riemann-Summe:

$c_n\approx\frac{1}{T}\sum_{k=0}^{N-1}\underbrace{f\left(k\cdot\frac{T}{N}\right)}_{= a_k}\cdot\ e^{i-\buildrel{\overbrace{\cdot\omega_n\cdot}}\over{\overbrace{\cdot\omega_n\cdot}}=n\cdot\frac{2\pi}{T}\left(k\cdot\frac{T}{N}\right)}\cdot\frac{T}{N}$

$=\frac{1}{N}\sum_{k=0}^{N-1}a_k\cdot\ e^{-2\pi i\cdot\frac{k\cdot n}{N}}=:{\hat{a}}_n$

Dies entspricht gerade der Berechnungsformel des n-ten Koeffizienten ${\hat{a}}_n$ der Diskreten Fourier Transformierten $\hat{a}=\left({\hat{a}}_0,{\hat{a}}_1,\ldots,{\hat{a}}_{N-1}\right)$ des Vektors $a\in\mathbb{C}^N$ .

Betrachtet man die Berechnungsformel des Koeffizienten ${\hat{a}}_{n+N}$ , so fällt auf, dass dieser dem Koeffizienten ${\hat{a}}_n$ entspricht, weshalb die diskrete Fourier-Transformierte nur zwischen ${\hat{a}}_0$ und ${\hat{a}}_{N-1}$ definiert ist:

${\hat{a}}_{n+N}=\frac{1}{N}\sum_{k=0}^{N-1}a_k\cdot e^{-2\pi i\cdot\frac{k\cdot\left(n+N\right)}{N}}=\frac{1}{N}\sum_{k=0}^{N-1}a_k\cdot e^{-2\pi i\cdot\frac{k\cdot n}{N}-2\pi i\cdot k}$

$=\frac{1}{N}\sum_{k=0}^{N-1}a_k\cdot e^{-2\pi i\cdot\frac{k\cdot n}{N}}\cdot\underbrace{e^{-2\pi i\cdot k}}_{=1}={\hat{a}}_n$

Von der kontinuierlichen zur Diskreten Fourier Transformation

Auch zur kontinuierlichen Fourier-Transformation besitzt die DFT große Ähnlichkeiten. Um das deutlich zu machen wird eine nichtperiodische Funktion f(t) betrachtet, die außerhalb des Intervalls $[0,\ T]$ verschwindet und auf diesem im Abstand $\triangle t=\frac{T}{N}$ jeweils als Funktionswert einen Eintrag aus $a{\in\mathbb{C}}^N$ annimmt:

$f\left(k\cdot\triangle t\right)=a_k$ , für $k=0,1,2,\ldots,N-1$

Sei nun die Zahl der untersuchten Werte N deutlich größer als die Länge des gewählten Intervalls $[0,\ T]$ , so lässt sich dort das Integral der Fourier-Transformierten $\hat{f}\left(\omega\right)$ der Funktion f sinnvoll durch eine diskrete Summe nähern:

$\hat{f}\left(\omega\right)=\int_{-\infty}^{\ \ \infty}{\ f\left(t\right)}{\cdot e}^{-i\cdot\omega\cdot t}dt\approx\sum_{k=0}^{\ \ N-1}{\ f\left(k\cdot\triangle t\right)}{\cdot e}^{-i\cdot\omega\cdot k\cdot\triangle t}\cdot\triangle t$

$=\sum_{k=0}^{\ \ N-1}{\ a_k}{\cdot e}^{-i\cdot\omega\cdot k\cdot\frac{T}{N}}\cdot\frac{T}{N}$

Wird diese Summe nur für $\omega=\omega_n=n\cdot\frac{2\pi}{T}$ berechnet, so ergibt sich:

$\hat{f}\left(\omega_n\right)\approx\sum_{k=0}^{\ \ N-1}{\ a_k}{\cdot e}^{-2\pi i\cdot\frac{k\cdot n}{N}}\cdot\frac{T}{N}$

Das entspricht bis auf den konstanten Faktor T der Berechnungsformel des n-ten Eintrags ${\hat{a}}_n$ der Diskreten Fourier Transformierten $\hat{a}$ .

IDFT: Inverse Diskrete Fourier Transformation

im Videozur Stelle im Video springen

Um zur Formel der Inversen DFT zu gelangen, kann die Fourier-Reihe $\mathfrak{F}[f]t$ derselben periodischen Funktion $f\left(t\right)$ betrachtet werden, welche oben beschrieben wurde.

$\mathfrak{F}[f](t)=\sum_{n = -\infty}^{\infty} {c_n\cdot e}^{i\cdot\omega_n\cdot t}}$

Im Fall der Diskreten Fourier Transformation werden die Koeffizienten c_n durch die Einträge ${\hat{a}}_n$ der Diskreten Fourier Transformierten repräsentiert. Da diese nur für n=0,...,N-1 definiert sind, läuft der Index in der Summe auch nur zwischen diesen beiden Grenzen. Berechnet man dementsprechend diese Reihe für die Werte $t=k\cdot\frac{T}{N}$ und für die Frequenzen $\omega_n=n\cdot\frac{2\pi}{T}$ , so erhält man folgendes Ergebnis:

$\mathfrak{F}\left[f\right]\left(k\cdot\frac{T}{N}\right)=\sum_{n=0}^{N-1}{\hat{a}}_n\cdot e^{i\cdot n\cdot\frac{2\pi}{T}\cdot k\cdot\frac{T}{N}}=\sum_{n=0}^{N-1}{\hat{a}}_n\cdot e^{2\pi i\cdot\frac{k\cdot n}{N}}=:a_k$

Definition: IDFT

Somit berechnen sich die Koeffizienten a_n der Inversen Diskreten Fourier Transformierten $a{\in\mathbb{C}}^N$ von $\hat{a}{\in\mathbb{C}}^N$ nach Umbenennung der Indizes auf folgende Art:

$a_n=\sum_{k=0}^{N-1}{\hat{a}}_k\cdot e^{2\pi i\cdot\frac{k\cdot n}{N}}$

Zur Zusammenfassung: Die Koeffizienten ${\hat{a}}_n$ der Diskreten Fourier Transformierten $\hat{a}{\in\mathbb{C}}^N$ von $a{\in\mathbb{C}}^N$ lauten:

${\hat{a}}_n=\frac{1}{N}\sum_{k=0}^{N-1}{a_k{\cdot e}^{-2\pi i\cdot\frac{k\cdot n}{N}}}$

Für den Vorfaktor $\frac{1}{N}$ bei der Diskreten Fourier Transformation gibt es unterschiedliche Konventionen. Manchmal wird er auch bei der Inversen DFT statt bei der DFT eingefügt.

Überblick Fourier Analysis

im Videozur Stelle im Video springen

Da nun die Diskrete Fourier Transforamtion und auch ihre Inverse bekannt sind, sollen beide noch einmal in den Kontext der Fourier-Analysis eingeordnet werden und ein kurzer Überblick über die drei wichtigsten Transformationen aus diesem Bereich gegeben werden. Dabei werden nun die in der Signalverarbeitung üblichen Bezeichnungen angewandt. Mit x soll ein Signal im Zeitbereich bezeichnet werden und mit X wird das entsprechende Signal im Frequenzbereich symbolisiert.

Überblick Fourier Analysis

DFT Matrix

Wird die Abkürzung $\zeta_N=e^{-2\pi i\cdot\frac{1}{N}}$ für die N-te Einheitswurzel eingeführt, so lauten die Formeln der Diskreten Fourier Transformation:

${\hat{a}}_n=\frac{1}{N}\sum_{k=0}^{N-1}{a_k{\cdot\zeta}_N^{k\cdot n}}$ DFT

$a_n=\sum_{k=0}^{N-1}{\hat{a}}_k\cdot\zeta_N^{-k\cdot n}$ IDFT

Im Folgenden werden die einzelnen Komponenten der DFT einmal ausgeschrieben:

${\hat{a}}_0=\frac{1}{N}\cdot\left(a_0\cdot1+\ a_1\cdot1\ +\ a_2\cdot1\ +...+\ a_{N-1}\cdot1\ \right)$

${\hat{a}}_1=\frac{1}{N}\cdot\left(a_0\cdot1+a_1{\cdot\zeta}_N^1+a_2{\cdot\zeta}_N^2+...+a_{N-1}{\cdot\zeta}_N^{N-1}\right)$

${\hat{a}}_2=\frac{1}{N}\cdot\left(a_0\cdot1+a_1{\cdot\zeta}_N^2+a_2{\cdot\zeta}_N^4+...+a_{N-1}{\cdot\zeta}_N^{2\cdot(N-1)}\right)$

$\ \ \ \ \ \ \ \vdots$

${\hat{a}}_{N-1}=\frac{1}{N}\cdot\left(a_0\cdot1+a_1{\cdot\zeta}_N^{N-1}+a_2{\cdot\zeta}_N^{(N-1)\cdot2}+...+a_{N-1}{\cdot\zeta}_N^{(N-1)\cdot(N-1)}\right)$

Dies lässt sich auch in Matrix-Schreibweise notieren:

$\left(\begin{matrix}{\hat{a}}_0\\{\hat{a}}_1\\{\hat{a}}_2\\\vdots\\{\hat{a}}_{N-1}\\\end{matrix}\right)=\frac{1}{N}\cdot\left(\begin{matrix}1&1&1&\ldots&1\\1&\zeta_N^1&\zeta_N^2&\ldots&\zeta_N^{N-1}\\1&\zeta_N^2&\zeta_N^4&\ldots&\zeta_N^{2(N-1)}\\\vdots&\vdots&\vdots&\ddots&\vdots\\1&\zeta_N^{N-1}&\zeta_N^{2(N-1)}&\ldots&\zeta_N^{(N-1)(N-1)}\\\end{matrix}\right)\left(\begin{matrix}a_0\\a_1\\a_2\\\vdots\\a_{N-1}\\\end{matrix}\right)$

Die dort auftretende Matrix

$Z=\left(\begin{matrix}1&1&1&\ldots&1\\1&\zeta_N^1&\zeta_N^2&\ldots&\zeta_N^{N-1}\\1&\zeta_N^2&\zeta_N^4&\ldots&\zeta_N^{2(N-1)}\\\vdots&\vdots&\vdots&\ddots&\vdots\\1&\zeta_N^{N-1}&\zeta_N^{2(N-1)}&\ldots&\zeta_N^{(N-1)(N-1)}\\\end{matrix}\right)$

wird als DFT-Matrix oder Fourier-Matrix bezeichnet. Es lässt sich zeigen, dass für ihre Inverse folgender Zusammenhang gilt:

$Z^{-1}=\frac{1}{N}\cdot\bar{Z}$ ,

wobei $\bar{Z}$ die komplex konjugierte Matrix von Z beschreibt.

Somit lauten die Formeln der DFT und der IDFT:

$\hat{a}=\frac{1}{N}\cdot Z\cdot a$ DFT
$a=N\cdot Z^{-1}\cdot\hat{a}=\bar{Z}\cdot\hat{a}$ IDFT

Eigenschaften der DFT

im Videozur Stelle im Video springen

Folgende Eigenschaft der DFT wurde bereits gezeigt. Würde der Koeffizient ${\hat{a}}_{n+N}$ berechnet werden, entspräche dieser dem Koeffizienten ${\hat{a}}_n$ der Diskreten Fourier Transformierten:

${\hat{a}}_{n+N}={\hat{a}}_n$

Des Weiteren gewinnt man mit der DFT nur Informationen für die Frequenzen $n\cdot\frac{2\pi}{T}$ mit $n=0,1,2,...,\frac{N}{2}$ . Es gilt nämlich:

${\hat{a}}_{N-n}=\frac{1}{N}\sum_{k=0}^{N-1}{a_k{\cdot e}^{-2\pi i\cdot\frac{k\cdot(N-n)}{N}}=\frac{1}{N}\sum_{k=0}^{N-1}a_k\cdot e^{2\pi i\cdot\frac{k\cdot n}{N}-2\pi i\cdot k}$

$=\frac{1}{N}\sum_{k=0}^{N-1}a_k\cdot e^{2\pi i\cdot\frac{k\cdot n}{N}}\cdot \underbrace{e^{-2\pi i\cdot k}}_{=1}=\bar{\hat{a_n}}$

Werden demnach Werte einer Signalfunktion $f\left(t\right)$ mit $0\le t\le T$ im Abstand $\triangle t=\frac{T}{N}$ , also mit der Abtastfrequenz $f_a=\frac{N}{T}$ ermittelt, so liefert die Diskrete Fourier Transformation nur Informationen zum Frequenzspektrum der Funktion für Frequenzen, die unter f_a/2 liegen.

Abtastfrequenz DFT Diskrete Frourier Transformation — Abtastfrequenz

Abtasttheorem

im Videozur Stelle im Video springen

Diese Erkenntnis wird im Abtasttheorem von Shannon zusammengefasst:

Sei $f\left(t\right)$ ein Signal, in dessen Frequenzspektrum f_s die höchste auftretende Frequenz ist. Dann ist dieses Signal vollständig durch seine Abtastwerte bestimmt, falls die Abtastfrequenz f_a größer als ${2\cdot f}_s$ ist. Die Frequenz $2\cdot f_s$ wird auch als Nyquist-Frequenz bezeichnet.

Linearität der DFT

Eine weitere leicht zu zeigende Eigenschaft der Diskreten Fourier Transformation ist die Linearität:

$\widehat{a_n+b_n}=\frac{1}{N}\sum_{k=0}^{N-1}{{(a}_k+b_k){\cdot e}^{-2\pi i\cdot\frac{k\cdot n}{N}}}$

$=\frac{1}{N}\sum_{k=0}^{N-1}{a_k{\cdot e}^{-2\pi i\cdot\frac{k\cdot n}{N}}}+\frac{1}{N}\sum_{k=0}^{N-1}{b_k{\cdot e}^{-2\pi i\cdot\frac{k\cdot n}{N}}}={\hat{a}}_n+{\hat{b}}_n$

Diskrete Fourier Transformation Beispiel

In diesem Beispiel soll das Signal $f\left(t\right)=t^5-10t^4+35t^3-50t^2+24t$ betrachtet werden und zu den Zeiten t=1/2, t=3/2, t=5/2 und t=7/2 abgetastet werden.

Die DFT ist also für den Vektor $a=\left(a_0,a_1,a_2,a_3\right)$ mit $a_0=f\left(1/2\right), a_1=f\left(3/2\right), a_2=f\left(5/2\right)$ und $a_3=f\left(7/2\right)$ durchzuführen. Der Vektor lautet somit:

$a=(3.28,\ -1.41,\ 1.41,\ -3.28)$

Mit der Formel für die DFT berechnet sich die Diskrete Fourier Transformierte mit N=4 wie folgt:

${\hat{a}}_0=\frac{1}{N}\cdot\left(a_0+\ a_1\ +\ a_2\ +\ a_3\ \right)=\frac{1}{4}\cdot\left(3,28-1,41+1,41-3.28\right)=0$

${\hat{a}}_1=\frac{1}{N}\cdot\left(a_0+a_1{\cdot\zeta}_N^1+a_2{\cdot\zeta}_N^2+a_3{\cdot\zeta}_N^3\right)=\frac{1}{4}\cdot\left(3,28-1,41\cdot e^{-\frac{2\pi i}{4}}+1,41\cdot e^{-\frac{4\pi i}{4}}-3,28\cdot e^{-\frac{6\pi i}{4}}\right)=\frac{1}{4}\cdot\left(3,28-1,41\cdot\left(-i\right)+1,41\cdot\left(-1\right)-3,28\cdot i\right)=\frac{1}{4}\cdot\left(1,87-1,87i\right)=0,47-0,47i$

${\hat{a}}_2=\frac{1}{N}\cdot\left(a_0+a_1{\cdot\zeta}_N^2+a_2{\cdot\zeta}_N^4+a_3{\cdot\zeta}_N^6\right)=\frac{1}{4}\cdot\left(3,28-1,41\cdot e^{-\pi i}+1,41\cdot e^{-2\pi i}-3,28\cdot e^{-3\pi i}\right)=\frac{1}{4}\cdot\left(3,28-1,41\cdot(-1)+1,41\cdot1-3,28\cdot(-1)\right)=\frac{1}{4}\cdot9,38=2,35$

${\hat{a}}_3=\frac{1}{N}\cdot\left(a_0+a_1{\cdot\zeta}_N^3+a_2{\cdot\zeta}_N^6+a_3{\cdot\zeta}_N^9\right)=\frac{1}{4}\cdot\left(3,28-1,41\cdot e^{-\frac{6\pi i}{4}}+1,41\cdot e^{-3\pi i}-3,28\cdot e^{-\frac{18\pi i}{4}}\right)=\frac{1}{4}\cdot\left(3,28-1,41\cdot i+1,41\cdot\left(-1\right)-3,28\cdot\left(-i\right)\right)=\frac{1}{4}\cdot\left(1,87+1,87i\right)=0,47+0,47i$

Die Diskrete Fourier Transformierte des Vektors $a=(3.28,\ -1.41,\ 1.41,\ -3.28)$ lautet also:

$\hat{a}=\left({\hat{a}}_0,{\hat{a}}_1,{\hat{a}}_2,{\hat{a}}_3\right)=(0,\ 0.47-0.47i,\ 2.35,\ 0.47+0.47i)$

Das Ergebnis lässt sich auch mithilfe der Fourier-Matrix berechnen. Das sieht dann folgendermaßen aus:

$\left(\begin{matrix}{\hat{a}}_0\\{\hat{a}}_1\\{\hat{a}}_2\\{\hat{a}}_3\\\end{matrix}\right)=\frac{1}{N}\cdot\left(\begin{matrix}1&1&1&1\\1&\zeta_N^1&\zeta_N^2&\zeta_N^3\\1&\zeta_N^2&\zeta_N^4&\zeta_N^6\\1&\zeta_N^3&\zeta_N^6&\zeta_N^9\\\end{matrix}\right)\left(\begin{matrix}a_0\\a_1\\a_2\\a_3\\\end{matrix}\right)$

Werden die passenden Werte eingesetzt, erhält man:

$\left(\begin{matrix}{\hat{a}}_0\\{\hat{a}}_1\\{\hat{a}}_2\\{\hat{a}}_3\\\end{matrix}\right)=\frac{1}{4}\cdot\left(\begin{matrix}1&1&1&1\\1&e^{-\frac{2\pi i}{4}}&e^{-\frac{4\pi i}{4}}&e^{-\frac{6\pi i}{4}}\\1&e^{-\frac{4\pi i}{4}}&e^{-\frac{8\pi i}{4}}&e^{-\frac{12\pi i}{4}}\\1&e^{-\frac{6\pi i}{4}}&e^{-\frac{12\pi i}{4}}&e^{-\frac{18\pi i}{4}}\\\end{matrix}\right)\left(\begin{matrix}3,28\\-1,41\\1,41\\-3,28\\\end{matrix}\right)=\left(\begin{matrix}0\\0,47-0,47i\\2,35\\0,47+0,47i\\\end{matrix}\right)$

zur Videoseite: DFT - Diskrete Fourier-Transformation

Beliebte Inhalte aus dem Bereich Höhere Analysis

Fourierreihen - Beispiel

Fourier Transformation

Fourier Transformation Übungsaufgabe I

Fourier Transformation Übungsaufgabe II

DFT - Diskrete Fourier-Transformation

FFT - Fast Fourier-Transformation

Hallo, leider nutzt du einen AdBlocker.

Auf Studyflix bieten wir dir kostenlos hochwertige Bildung an. Dies können wir nur durch die Unterstützung unserer Werbepartner tun.

Schalte bitte deinen Adblocker für Studyflix aus oder füge uns zu deinen Ausnahmen hinzu. Das tut dir nicht weh und hilft uns weiter.

Danke!
Dein Studyflix-Team

Wenn du nicht weißt, wie du deinen Adblocker deaktivierst oder Studyflix zu den Ausnahmen hinzufügst, findest du hier eine kurze Anleitung. Bitte .