Video anzeigen

Vollständige Induktion

Wichtige Inhalte in diesem Video

Du willst wissen, was vollständige Induktion ist und wie du damit einen Beweis führen kannst? Dann bist du hier genau richtig! Schau dir unser Video dazu an!

Inhaltsübersicht

Vollständige Induktion einfach erklärt

zur Stelle im Video springen

(00:13)

Die vollständige Induktion ist ein Beweisverfahren, mit dem du Aussagen für die ganzen natürlichen Zahlen beweisen kannst. Das funktioniert wie bei einer Reihe von Dominosteinen. Du schubst den ersten Stein an und musst dann nur noch dafür sorgen, dass der jeweils nächste Stein umgestoßen wird.

Vollständige Induktion

1.) Induktionsanfang: Zeige, dass die Aussage für den Startwert gilt (meistens n=1 )
2.) Induktionsschritt: Dieser besteht aus:

Induktionsvoraussetzung oder Induktionsannahme: Ab jetzt gehst du davon aus, dass die Aussage für ein beliebiges $n \in \mathbb{N}$ gilt.
Induktionsbehauptung: Hier sagst du einfach, dass die Aussage dann auch für gelten muss.
Induktionsschluss: Jetzt zeigst du mit Hilfe der Induktionsvoraussetzung, dass die Aussage tatsächlich auch für gilt.

Mit der vollständigen Induktion kannst du eine ganze Reihe von unterschiedlichen Aussagen beweisen, wobei das Prinzip immer das Gleiche bleibt.

Vollständige Induktion Beispiel

zur Stelle im Video springen

(00:52)

Ein ganz berühmtes Beispiel für einen Induktionsbeweis ist die Summenformel von Gauß. Dabei sollst du zeigen, dass für alle $n \in \mathbb{N}$ gilt

$\(\sum \limits_{k=1}^n k =1+2+3+\cdots = \frac{n(n+1)}{2}$ .

1.) Induktionsanfang

Wir beginnen mit einem Startwert und zeigen, dass die Aussage für dieses kleine n richtig ist. In diesem Fall beginnst du mit dem Startwert n=1 .

$\(\sum \limits_{k=1}^1 k = 1=\frac{1(1+1)}{2} = \frac{2}{2}=1$

Beide Seiten sind gleich, die Aussage gilt also für n=1 .

2.) Induktionsschritt

Induktionsvoraussetzung/Induktionsannahme

Hier behauptest du, dass die Aussage für ein beliebiges n gilt. Stell dir einfach vor, du würdest irgendeine beliebige Zahl heraussuchen und festhalten.

Es sei $\(\sum \limits_{k=1}^n k = \frac{n(n+1)}{2}$ für ein beliebiges $n \in \mathbb{N}$ .

Induktionsbehauptung

Hier definierst du sozusagen deinen Zielpunkt. Du wiederholst die Aussage, die du beweisen möchtest, und setzt für jedes n einfach n+1 ein.

Dann gilt für n+1 : $\(\sum \limits_{k=1}^{n+1} k = \frac{(n+1)((n+1)+1)}{2} = \frac{(n+1)(n+2)}{2}$ .

Induktionsschluss

Jetzt kommt der eigentliche Beweis. Du startest beim linken Teil der Induktionsbehauptung und landest durch Termumformung bei der rechten Seite. Dabei verwendest du an irgendeinem Punkt die Induktionsvoraussetzung, also dass die Gleichung für n gilt.

Lass uns das einmal gemeinsam durchgehen.

$\(\sum \limits_{k=1}^{n+1} k = \(\sum \limits_{k=1}^n k + (n+1)$

Zuerst ziehst du die Summe über die ersten n Zahlen heraus. Damit kannst du jetzt nämlich die Summenformel einsetzen, denn laut Induktionsvoraussetzung gilt sie für n.

$\(\sum \limits_{k=1}^n k + (n+1) = \frac{n(n+1)}{2} + (n+1)=\frac{n(n+1)}{2} + \frac{2(n+1)}{2}$

$= \frac{n(n+1)+(2n+2)}{2}$

$= \frac{n^2+n+2n+2}{2}$

$= \frac{(n+1)(n+2)}{2}$

$= \frac{(n+1)((n+1)+1)}{2}$

Nach dem Einsetzen der Induktionsvoraussetzung fasst du geschickt zusammen und formst die Gleichung um. Damit hast du jetzt also gezeigt, dass gilt

$\(\sum \limits_{k=1}^{n+1} k = \frac{(n+1)((n+1)+1)}{2}$ .

Das ist genau die Induktionsbehauptung. Die Summenformel gilt also für n=1 , für ein beliebiges n und für n+1. Damit gilt die Gleichung für alle $n \in \mathbb{N}$ und du hast erfolgreich die Gaußsche Summenformel bewiesen.

Hinweis: Noch mehr Beispiele findest du in unserem Video Vollständige Induktion Aufgaben !

Zum Video: Vollständige Induktion Aufgaben

Vollständige Induktion Prinzip und Tricks

Also eigentlich ist es gar nicht so schwer, einen Induktionsbeweis mit vollständiger Induktion zu führen. Es gibt noch ein paar Tricks, mit denen du dir das Leben leichter machen kannst.

Einen Beweis mit vollständiger Induktion erkennst du meistens daran, dass eine Aussage von einer natürlichen Zahl n abhängt und für alle natürlichen Zahlen gelten soll.
Beim Induktionsanfang startest du in den allermeisten Fällen mit , es gibt aber auch Ausnahmen.
Falls du bei den Umformungen mal nicht weiterkommst, dann starte einfach von der rechten Seite der Gleichung aus. Irgendwann treffen sich die beiden Rechnungen und dann kannst du die Umformung sauber von links nach rechts aufschreiben.
Versuche außerdem immer möglichst früh so umzuformen, dass du die Induktionsvoraussetzung benutzen kannst. Damit bist du eigentlich immer auf dem richtigen Weg.

Das Prinzip bleibt dabei immer das gleiche. Du startest mit dem Induktionsanfang, also dem Umstoßen des ersten Dominosteins. Für eine kleine Zahl testest du damit, ob die Aussage überhaupt stimmt.

Im weiteren Verlauf machst du den Induktionsschritt. Dafür behauptest du einfach, dass die Aussage für ein beliebiges n gilt (Induktionsannahme). Darauf aufbauend beweist du allgemein, dass die Aussage dann auch für n+1 gelten muss (Induktionsbehauptung und Induktionsschluss). Mit diesem Schritt kannst du dann quasi jeden Dominostein erreichen.

Vorteile der vollständigen Induktion

Mit der vollständigen Induktion kannst du also ganz schnell Aussagen für alle natürlichen Zahlen beweisen. Ohne dieses Prinzip müsstest du zum Beispiel die Summenformel für jede Zahl einmal nachrechnen.

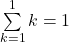$\(\sum \limits_{k=1}^1 k = 1$ und $\frac{1(1+1)}{2}=1$

$\(\sum \limits_{k=1}^2 k = 1+2 = 3$ und $\frac{2(2+1)}{2} = \frac{6}{2}=3$

$\(\sum \limits_{k=1}^3 k = 1+2+3=6$ und $\frac{3(3+1)}{6}=\frac{12}{2}=6$

usw.

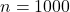Das wäre eine Menge Arbeit, vor allem, weil es unendlich viele natürliche Zahlen gibt. Mit dem Induktionsschritt von zu n+1 sparst du dir diese Arbeit. Denn damit zeigst du, dass du von jeder beliebigen natürlichen Zahl auf ihren Nachfolger schließen kannst. Wenn die Formel also für n=2 gilt, dann gilt sie auch für n+1=3 . Oder für n=1000 und n+1=1001 und so weiter. Mit der vollständigen Induktion geht es also viel schneller und du musst die Formel nicht für unendlich vielen Zahlen testen.