Partielle DGL
Du möchtest wissen, was eine partielle Differentialgleichung ist? Dann bist du hier genau richtig! Im folgenden erklären wir dir diese besondere Form der Differentialgleichungen.
Inhaltsübersicht
Partielle Differentialgleichung Definition und Abgrenzung zu gewöhnlichen Differentialgleichungen
Wie du weißt, hängt bei gewöhnlichen Differentialgleichungen die unbekannte Funktion y nur von einer Variablen x ab, zum Beispiel von einem Ort. Jetzt kann es aber sein, dass dich ein Zustand y nicht nur für verschiedene Orte, sondern auch für unterschiedliche Zeitpunkte interessiert. Dafür brauchst du partielle Differentialgleichungen, in denen y eine Funktion mehrerer Variablen ist und auch nach mehreren Variablen partiell abgeleitet wird.
Partielle Differentialgleichung Aufbau und Formel
Eine partielle Differentialgleichung für  , also für zwei Variablen, sieht dann so aus:
, also für zwei Variablen, sieht dann so aus:

Hier ist F eine Funktion von x1, x2, y und den partiellen Ableitungen nach x1 und x2. Partielle Ableitungen zweiter Ordnung können zweite Ableitungen nach ein- und derselben Variable sein wie:

oder gemischte Ableitungen nach verschiedenen Variablen, so wie:
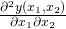
Natürlich kann y auch eine Funktion von n Variablen x1, x2, …, xn sein:

Dann sieht die DGL so aus:

Aus Übersichtsgründen haben wir die Abhängigkeiten in Klammern weggelassen.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Partielle DGL Beispiel: eindimensionale Transportgleichung
Zu guter Letzt noch ein Beispiel: die eindimensionale Transportgleichung

Diese Gleichung beschreibt den Transport eines Stoffes mit Konzentration c(x, t) in einer inkompressiblen Flüssigkeit mit Strömungsgeschwindigkeit v(x, t). x gibt den Ort und t die Zeit an.
Du hast partielle Differentialgleichungen kennengelernt und das Beispiel der Transportgleichung gesehen.


