Taylorreihe Sinus
Du weißt zwar, wie du theoretisch eine Taylorreihe berechnen kannst, die Taylorreihe Sinus bereitet die aber noch Probleme? In diesem Beitrag erklären wir dir Schritt für Schritt die Taylorreihe der Sinusfunktion.
Inhaltsübersicht
Taylorentwicklung Sinus: Ableitungen und Entwicklung des Taylor-Polynoms
Wir betrachten nun also die Sinusfunktion von x und einen Entwicklungspunkt von  . Davon bilden wir nun die verschiedenen Taylorpolynome und die erste Ableitung.
. Davon bilden wir nun die verschiedenen Taylorpolynome und die erste Ableitung.
Die Ableitung von Sinus x ist Cosinus x. Der Cosinus an der Stelle Null ist 1. Damit kannst du schon das Taylorpolynom  aufstellen.
aufstellen.


 an der Stelle
an der Stelle  ist Sinus von Null und das ergibt wiederum Null.
ist Sinus von Null und das ergibt wiederum Null.  an der Stelle Null ist Cosinus von Null. Daraus resultiert als Ergebnis Eins. Für
an der Stelle Null ist Cosinus von Null. Daraus resultiert als Ergebnis Eins. Für  setzen wir auch in der Differenz Null ein.
setzen wir auch in der Differenz Null ein.  ist gleich
ist gleich  . Schauen wir uns das doch mal graphisch an.
. Schauen wir uns das doch mal graphisch an.
Die blaue Kurve ist der Sinus und die orangefarbene das Taylorpolynom zweiten Grades. Du kannst erkennen, dass die orangene Kurve die Tangente an den Funktionsgraphen im Entwicklungspunkt ist.
Taylorreihe Sinus: Zweite und dritte Ableitung
Nun bilden wir die nächsten zwei Ableitungen und werten sie wieder an der Stelle Null aus.


Die zweite Ableitung ist Minus der Sinus und ergibt an der Stelle Null, Null. Dieser Faktor gehört zum quadratischen Glied des Taylor-Polynoms, also hat das Taylor-Polynom keinen quadratischen Anteil. Auch das konstante Glied des Taylor-Polynoms war am Entwicklungspunkt Null, denn  . Konstanten und quadratische Terme sind gerade Funktionen, der Sinus ist jedoch eine ungerade Funktion. Daher kann auch das Taylor-Polynom des Sinus keinerlei gerade Terme enthalten.
. Konstanten und quadratische Terme sind gerade Funktionen, der Sinus ist jedoch eine ungerade Funktion. Daher kann auch das Taylor-Polynom des Sinus keinerlei gerade Terme enthalten.
Wir wissen schon jetzt, dass die zweite, vierte, sechste und die weiteren Ableitungen ausgewertet an der Stelle Null alle wegfallen werden. Da somit 
 entspricht, können wir direkt
entspricht, können wir direkt 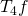 aufstellen, um eine bessere Approximation zu erhalten.
aufstellen, um eine bessere Approximation zu erhalten.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Taylorreihe Sinus: Taylor-Polynom vierten Grades
Es ergibt sich das hier:
Die ersten zwei Glieder kannst du getrost von vorher abschreiben. Die zweite Ableitung ist Null, wie wir festgestellt haben, sodass der quadratische Term wegfällt. Wir setzen -1 für die dritte Ableitung ein, teilen durch  , also durch sechs, und erhalten
, also durch sechs, und erhalten 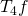 als
als  .
.
Auch das plotten wir und wir sehen, dass sich schon eine bessere Approximation ergibt. Der gelbe Graph nähert sich dem Verlauf der blauen Sinus-Kurve an.
Als nächstes plotten wir  . Versuch doch mal, das Polynom selbst aufzustellen. Kommst du auch auf
. Versuch doch mal, das Polynom selbst aufzustellen. Kommst du auch auf

Schau dir den lila Kurvenverlauf an. Die Annäherung ist nochmals genauer geworden. Gehen wir jetzt noch zwei Ordnungen höher, ist die Abweichung kaum mehr zu erkennen, wie du im Graph siehst. Die grüne und blaue Kurve sind kaum zu unterscheiden.
Sinus Taylorreihe: Einführung des Landau-Symbols
Du kannst auch

schreiben. Dabei ist  das Landau-Symbol. Allgemein gilt:
das Landau-Symbol. Allgemein gilt:

Wenn du das Taylor-Polynom m-ten Grades aufgestellt hast, kannst du den Fehler zur Funktion  , also alle fehlenden Potenzen ab der Ordnung
, also alle fehlenden Potenzen ab der Ordnung  , mithilfe des Landau-Symbols
, mithilfe des Landau-Symbols  zusammenfassen zu
zusammenfassen zu  . Dabei steht
. Dabei steht  für eine beliebige Funktion, die mindestens den Faktor
für eine beliebige Funktion, die mindestens den Faktor  enthält. Genauer heißt das: Wenn du eine Funktion in der Form
enthält. Genauer heißt das: Wenn du eine Funktion in der Form  ausdrücken, also
ausdrücken, also  ausklammern kannst, schreibst du
ausklammern kannst, schreibst du 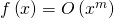 . Dabei muss gelten, dass
. Dabei muss gelten, dass  im Ursprung stetig ist.
im Ursprung stetig ist.
Hier einige Beispiele zum Verständnis. Beim ersten Beispiel kann  ausgeklammert werden. Der Vorfaktor 5 ist eine konstante Funktion, die im Ursprung stetig ist. Klammerst du
ausgeklammert werden. Der Vorfaktor 5 ist eine konstante Funktion, die im Ursprung stetig ist. Klammerst du  aus, erhältst du für
aus, erhältst du für  . Diese Funktion ist im Ursprung nicht stetig und somit gilt
. Diese Funktion ist im Ursprung nicht stetig und somit gilt  .
.  lässt sich nämlich ausklammern und
lässt sich nämlich ausklammern und  ergibt eine stetige Funktion.
ergibt eine stetige Funktion.
Wenden wir uns dem nächsten Beispiel zu. Du musst dir lediglich den Term niedrigster Ordnung ansehen. Das ist in diesem Fall  . Die übrigen Terme
. Die übrigen Terme  und
und  sind ebenfalls in
sind ebenfalls in  , da du auch hier
, da du auch hier  ausklammern kannst. Kommen wir nun zurück zu unserer Taylorreihe des Sinus:
ausklammern kannst. Kommen wir nun zurück zu unserer Taylorreihe des Sinus:

Diese Schreibweise bedeutet also, dass der Sinus aus den Termen  und einem Restglied aus Termen mindestens 5. Ordnung beschrieben werden kann.
und einem Restglied aus Termen mindestens 5. Ordnung beschrieben werden kann.





