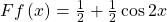Fourierreihen – Beispiel
Du hast die Fourierreihen nun hoffentlich verstanden und kannst dir das Ganze nun an zwei Beispielen genauer ansehen.
Inhaltsübersicht
Fourierreihen – Beispiel und Erklärung
Unser erstes Beispiel ist diese periodische Funktion.

Es ist eine unstetige Funktion, die aus Geraden auf Abschnitten der Länge  besteht.
besteht.
Außerdem handelt es sich um eine ungerade Funktion, also kannst du schon jetzt folgern, dass alle  sind. Die Koeffizienten
sind. Die Koeffizienten  kannst du nach der Formel für die Koeffizienten in der Fourierreihe berechnen.
kannst du nach der Formel für die Koeffizienten in der Fourierreihe berechnen.

![Rendered by QuickLaTeX.com =\frac{1}{\pi}\left[\frac{\sin{nx}-nx\cos{nx}\ }{n^2}\right]_{-\pi}^\pi=\frac{2(\sin{n\pi}-n\pi\cos{n\pi})\ }{\pi n^2}=\left(-1\right)^{n+1}\frac{2}{n}](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-cd9871a6dad6490a6e6e1fb9419e1fe5_l3.png)
Integral bestimmen
Für  setzt du
setzt du  ein und bestimmst das Integral und wertest es aus. Der Sinus von
ein und bestimmst das Integral und wertest es aus. Der Sinus von  ist immer Null. Der Kosinus von
ist immer Null. Der Kosinus von  ist abwechselnd Eins und minus Eins. Das
ist abwechselnd Eins und minus Eins. Das  und ein n kürzen sich heraus und es bleibt
und ein n kürzen sich heraus und es bleibt  . Also ergibt sich folgende Fourierreihe:
. Also ergibt sich folgende Fourierreihe:

Als nächstes wollen wir uns die Fourier-Polynome mal ansehen. Das erste Fourierpolynom ist  und ergibt sich zu
und ergibt sich zu  :
:
Der einzelne blau dargestellte Sinus kann die schwarze Funktion nicht zufriedenstellend nachbilden. Daher bestimmen wir  :
:

Der orangefarbene Graph ist schon eine bessere Approximation. Jetzt machen wir größere Schritte. Wir bestimmen  .
.

Wie wir an der gelben Kurve erkennen können, ist die Approximation wieder besser geworden.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Fourierreihe – zweites Beispiel
Machen wir noch ein zweites Beispiel. Hast du dich schon immer gefragt, wie man trigonometrische Formeln wie  eigentlich beweisen kann? Mit Fourierreihen geht das und wir zeigen dir wie.
eigentlich beweisen kann? Mit Fourierreihen geht das und wir zeigen dir wie.
Zunächst definieren wir uns unsere Funktion  . Es ist eine gerade Funktion, somit fallen alle Koeffizienten
. Es ist eine gerade Funktion, somit fallen alle Koeffizienten  weg.
weg.  bestimmst du so:
bestimmst du so:
Das Integral ist etwas kompliziert zu berechnen und soll hier nicht im Fokus stehen. Das Ergebnis ist Null für alle  und nur für
und nur für  ergibt sich der Wert
ergibt sich der Wert  . Du musst nur noch
. Du musst nur noch  bestimmen. Dazu wollen wir dir einen Trick zeigen. Sieh dir mal die Funktion Cosinus Quadrat auf dem Intervall
bestimmen. Dazu wollen wir dir einen Trick zeigen. Sieh dir mal die Funktion Cosinus Quadrat auf dem Intervall  genau an.
genau an.
Sie muss in Summe mit dem Sinus Quadrat immer 1 ergeben, denn es gilt  .
.
Außerdem wissen wir, dass  entspricht, denn die Funktionen sind
entspricht, denn die Funktionen sind  -periodisch und nur entlang der x-Achse zueinander verschoben. Daraus können wir folgern, dass das Integral
-periodisch und nur entlang der x-Achse zueinander verschoben. Daraus können wir folgern, dass das Integral  genau den Wert der Hälfte der rechteckigen Fläche annimmt.
genau den Wert der Hälfte der rechteckigen Fläche annimmt.

Diese ist  lang und eins hoch. Es ergibt sich
lang und eins hoch. Es ergibt sich  .
.
Zum Schluss kannst du deine Ergebnisse zur Fourierreihe zusammensetzen: