DGL 1. & 2. und höherer Ordnung
Differentialgleichungen lassen sich nach ihrem Grad ordnen. So spricht man von Differentialgleichungen erster, zweiter und n-ter Ordnung. Was es mit diesen Begriffen genau auf sich hat, lernst du hier!
Inhaltsübersicht
Differentialgleichungen erster, zweiter und höherer Ordnung Definition und Beispiele
Schauen wir uns zu Beginn nochmal die allgemeine Formel der gewöhnlichen Differentialgleichung an:
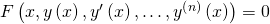
Dabei bestimmt die höchste vorkommende Ableitung n die Ordnung der DGL.
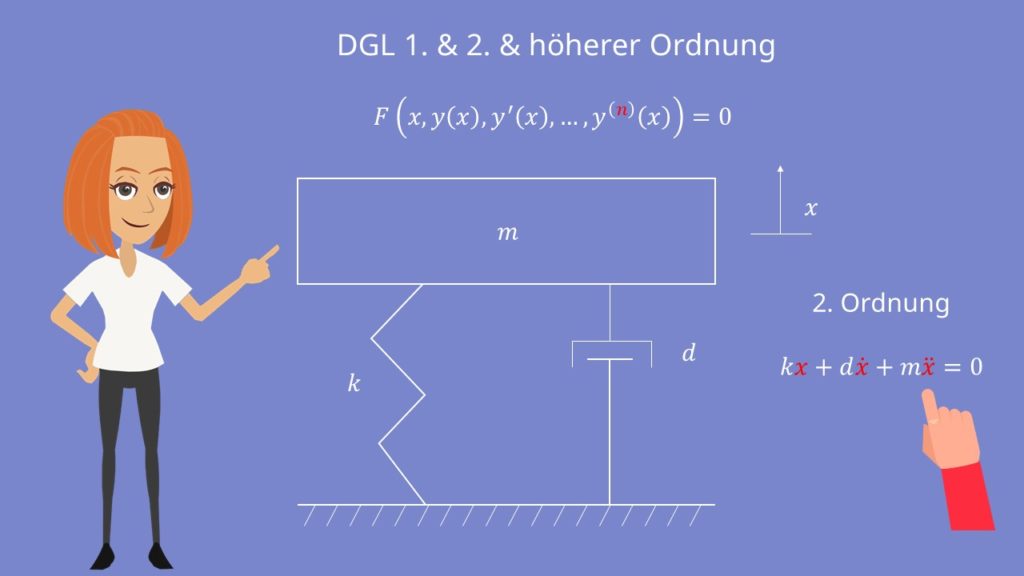
Differentialgleichung 2. Ordnung Beispiel: Feder-Masse-Dämpfer-System
Ein Beispiel für gewöhnliche Differentialgleichungen ist das Feder-Masse-Dämpfer-System. Hier gibt k die Federsteifigkeit an, d die Dämpferkonstante und m die Masse. In der DGL kommen die Position x, die Geschwindigkeit 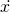 und die Beschleunigung
und die Beschleunigung 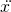 vor.
vor.
Von diesen ist die zweite Ableitung von x, also 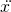 , die höchste vorkommende Ableitung. Somit ist es eine DGL zweiter Ordnung.
, die höchste vorkommende Ableitung. Somit ist es eine DGL zweiter Ordnung.
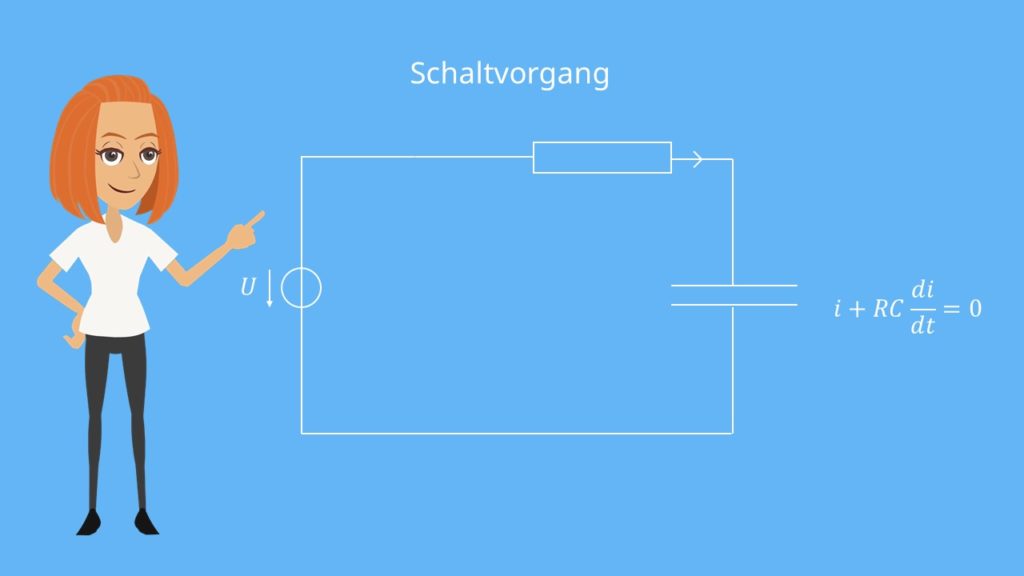
Differentialgleichung 1. Ordnung Beispiel: Schaltvorgang
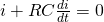
Ein weiteres Beispiel für eine gewöhnliche DGL stellt der Schaltvorgang dar. Hier kannst du feststellen, dass die erste Ableitung die Höchste ist.
Schauen wir uns noch kurz die Variablen an: i ist der Strom, R der Widerstand und C die Kapazität des Kondensators. Hier liegt also eine DGL erster Ordnung vor.
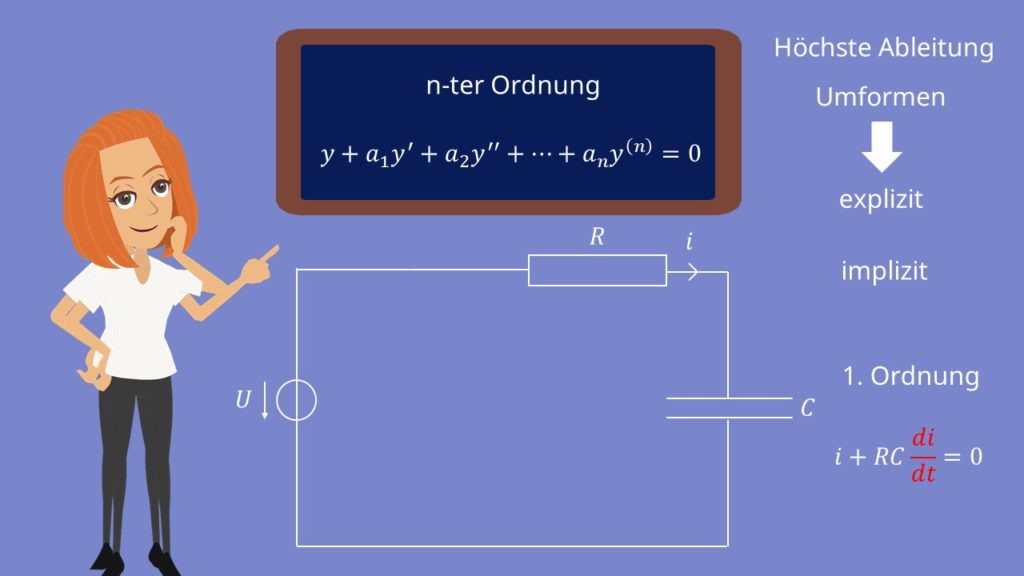
Differentialgleichung n-ter Ordnung und explizite und implizite DGL
Natürlich kann deine Differentialgleichung auch so aussehen:
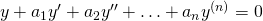
Das ist dann eine Differentialgleichung n-ter Ordnung.
Kommen wir noch zu einem Fachbegriff an dieser Stelle: Ist die DGL nach der höchsten Ableitung aufgelöst oder lässt sie sich so umformen, dass sie nach der höchsten Ableitung aufgelöst ist, so heißt sie explizit. Andernfalls heißt sie implizit.
Damit weißt du jetzt auch, wie du die Ordnung einer Differentialgleichung bestimmst und was eine explizite und implizite Differentialgleichung ist.