Anfangswertproblem
Du möchtest wissen, was es mit dem Anfangswertproblem auf sich hat, wann es eintritt und wie es sich lösen lässt? In diesem Beitrag erklären wir es dir.
Inhaltsübersicht
Lösen einer Differentialgleichung mithilfe der e-Funktion
Wenn du eine Differentialgleichung löst, erhältst du zunächst eine allgemeine Lösung. Nehmen wir an, wir haben die folgende Differentialgleichung gegeben:
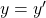
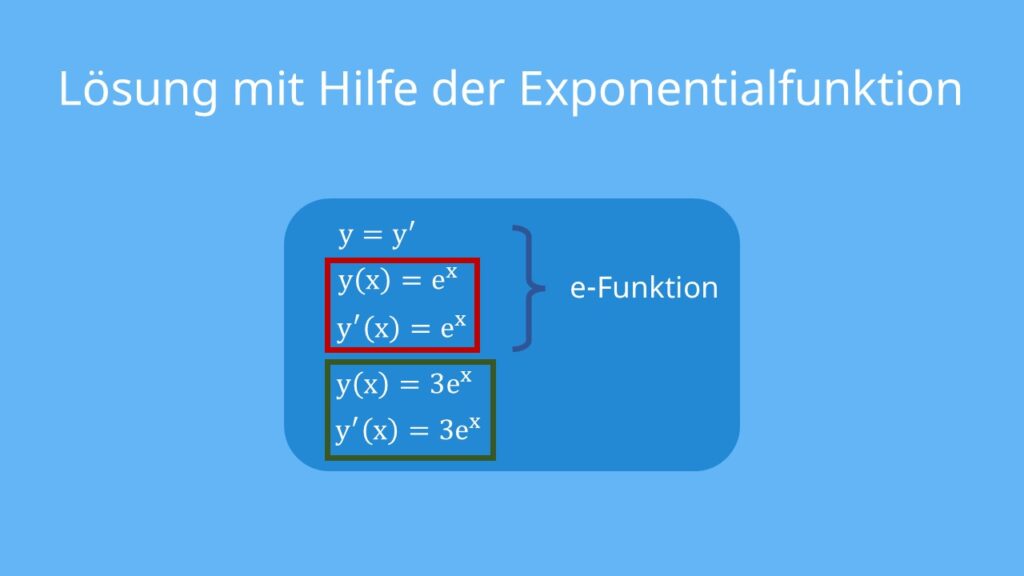
Diese Gleichung wird gelöst durch die Exponentialfunktion, denn hier ist die Funktion genau gleich, wie ihre Ableitung:
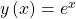
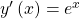
Also löst die e-Funktion die Differentialgleichung. Aber ist das die einzige Lösung?
Wenn man den Lösungsansatz
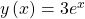
wählt, ergibt sich die Ableitung:
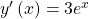
Das neue y löst die Differentialgleichung ebenso. Du kannst die e-Funktion sogar mit einer beliebigen Konstante multiplizieren
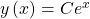
und erhältst unendlich viele Lösungen beziehungsweise die allgemeine Lösung.
Bestimmen eines Anfangswerts
Um jetzt die eindeutige Lösung bestimmen zu können, benötigst du noch einen Anfangswert. Der könnte
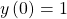
sein. Anfangswert bedeutet, dass man den Anfangszustand kennt. Es gibt viele Differentialgleichungen in Zeit, bei denen die Beschreibung eines Phänomens ab dem Zeitpunkt Null läuft.
Wir setzen zunächst in die allgemeine Lösung ein
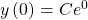
Wie du weißt ist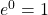 
somit ergibt sich:
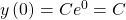
Dann setzen wir dies mit dem Anfangswert gleich.
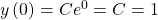
Aufgelöst nach C
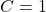
ergibt sich C ist gleich Eins.
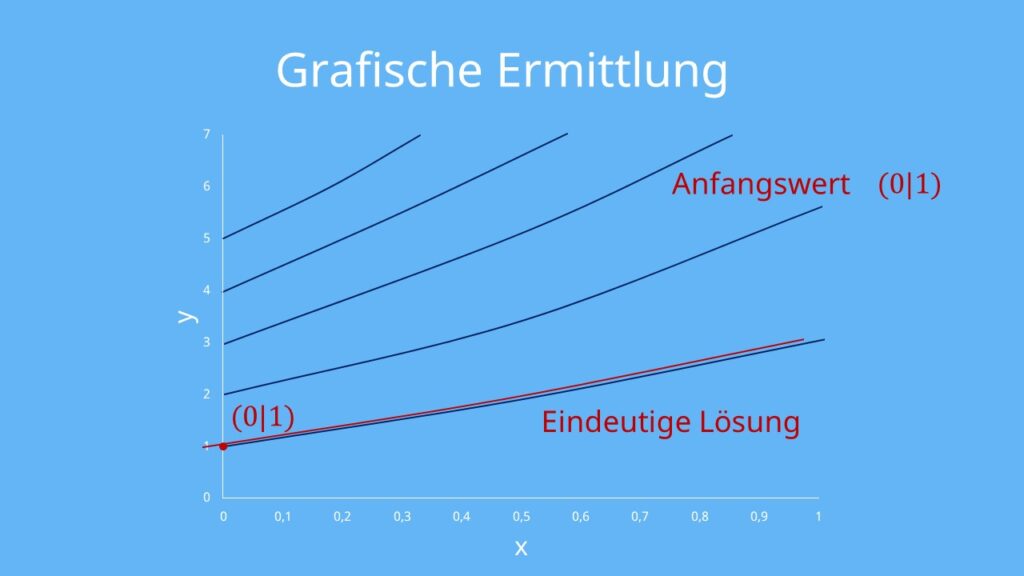
Grafische Veranschaulichung und Eindeutige Lösung
Schauen wir uns am besten ein paar Lösungskurven an. Dann zeichnen wir den Anfangswert ein: x = 0 und y = 1. Nun wissen wir, dass die Lösungskurve, die durch unseren Anfangswert geht, unsere eindeutige Lösung ist.
Wenn du eine Differentialgleichung höherer Ordnung löst, brauchst du entsprechend viele Anfangswerte. Eine DGL n-ter Ordnung bedarf n Anfangswerte.
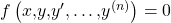
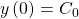
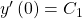
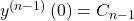
Eine Differentialgleichung zusammen mit ihren Anfangsbedingungen heißt Anfangswertproblem.
Super. Jetzt kennst du dich mit Anfangswertproblemen aus, weißt, was sie grafisch bedeuten und wie viele Anfangsbedingungen du bei Differentialgleichungen höherer Ordnung benötigst.