Video

Quiz

Trennung der Variablen

Du möchtest wissen, wie die Methode der Trennung der Variablen funktioniert? Im Folgenden zeigen wir dir, was trennbare Differentialgleichungen sind und wie du sie mithilfe der Trennung der Variablen lösen kannst.

Inhaltsübersicht

Lösung von homogenen Differentialgleichungen

Die Methode der Trennung der Variablen wird auch häufig als Trennung der Veränderlichen, Separation der Variablen oder Separationsmethode bezeichnet. Du kannst dieses Verfahren anwenden, wenn du eine homogene gewöhnliche Differentialgleichung erster Ordnung in folgender Form schreiben kannst:

$y^\prime=f\left(x\right)g(y)$

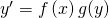
Die DGL heißt dann trennbar oder separierbar. 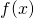f(x) fasst alle von 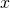abhängigen Anteile zusammen und 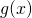g(x) enthält alle von 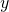abhängigen Anteile. 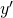$y^\prime$ ist die Ableitung von 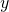nach 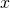, die du auch so darstellen kannst:

Trennung der Variablen

Im nächsten Schritt sortierst du. Der Term links vom Gleichheitszeichen ist nur noch direkt von 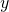abhängig, rechts kommt nur noch 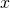vor.

$\frac{dy}{g\left(y\right)}=f\left(x\right)dx$

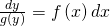
Separation der Variablen: Bestimmte und unbestimmte Integration

Jetzt kannst du integrieren. Dafür hast du zwei Möglichkeiten. Entweder integrierst du unbestimmt und kümmerst dich erst später um die auftretende Konstante C oder du integrierst bestimmt und setzt die Anfangswerte als untere Grenzen ein.

Trennung der Variablen: Bestimmte und unbestimmte Integration — Bestimmte und unbestimmte Integration

Beides hat Vor- und Nachteile. Die direkte Integration spart dir am Ende Arbeit, weil du die Anfangswerte nicht mehr einsetzen musst, um C zu bestimmen. Sie ist allerdings unübersichtlicher. Letztendlich ist es Geschmackssache, welche Integrationsmethode du bevorzugst. Nachdem du die Stammfunktionen bestimmt hast, kannst du die Gleichung nach y auflösen und erhältst deine Lösung.

Quiz zum Thema Trennung der Variablen

Beispiel

Üben wir das am besten gemeinsam an einem Beispiel. Wir haben folgende Differentialgleichung:

$y^\prime=\frac{x}{y}$

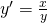
Gehen wir nun die einzelnen Schritte durch. Du kannst 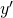$y^\prime$ umschreiben zu 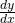$\frac{dy}{dx}$ . Danach sortierst du alle 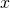nach rechts und alle 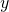auf die linke Seite des Gleichheitszeichens. Jetzt kannst du beide Seiten integrieren.

Trennung der Variablen: Beispiel — Beispiel

Wir entscheiden uns für die unbestimmte Integration, um einen besseren Überblick zu behalten.

$\frac{y^2}{2}=\frac{x^2}{2}+C$

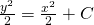
Jetzt können wir die DGL nach y umstellen. Das ist die allgemeine Lösung der DGL. Die eindeutige Lösung erhältst du mit einer Anfangsbedingung. Sagen wir, unsere Anfangsbedingung ist:

$y\left(0\right)=1$

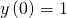
Diese setzt du in die Gleichung der allgemeinen Lösung ein. Du quadrierst beide Seiten und teilst durch zwei, sodass sich 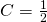$C=\frac{1}{2}$ ergibt. Damit ist deine eindeutige Lösung:

Beispiel

Um sicher zu gehen, dass du alles richtig gemacht hast, kannst du eine Probe machen. Dafür leitest du 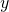ab, indem du die Kettenregel anwendest.

$y^\prime=\frac{1}{2\sqrt{x^2+1}}\ast\ 2x=\frac{x}{\sqrt{x^2+1}}$

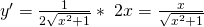
Erst leitest du die Wurzel ab und dann bildest du die innere Ableitung von 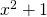x^2+1 . Sie ist 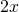. Das fasst du zusammen. Setze jetzt die Ableitung in die ursprüngliche DGL 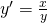$y^\prime=\frac{x}{y}$ ein.

$y^\prime=\frac{x}{\sqrt{x^2+1}}=\frac{x}{y}=\frac{x}{\sqrt{x^2+1}}$

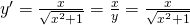
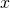im Zähler bleibt stehen und für 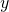im Nenner setzt du 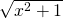$\sqrt{x^2+1}$ ein. Die Ausdrücke sind gleich. Wir haben alles richtig gemacht. Jetzt kennst du die trennbaren Differentialgleichungen und du weißt, wie du sie lösen kannst.

zur Videoseite: Trennung der Variablen

Beliebte Inhalte aus dem Bereich Höhere Analysis

Intro Gewöhnliche Differentialgleichungen lösen

Trennung der Variablen

Variation der Konstanten

Ansatz vom Typ der rechten Seite / Störfunktion

Transformation in System 1. Ordnung

Fundamentalsystem - Wronski-Determinante

Hallo, leider nutzt du einen AdBlocker.

Auf Studyflix bieten wir dir kostenlos hochwertige Bildung an. Dies können wir nur durch die Unterstützung unserer Werbepartner tun.

Schalte bitte deinen Adblocker für Studyflix aus oder füge uns zu deinen Ausnahmen hinzu. Das tut dir nicht weh und hilft uns weiter.

Danke!
Dein Studyflix-Team

Wenn du nicht weißt, wie du deinen Adblocker deaktivierst oder Studyflix zu den Ausnahmen hinzufügst, findest du hier eine kurze Anleitung. Bitte .