Reihenschaltung und Parallelschaltung
Grundsätzlich gibt es zwei verschiedene Möglichkeiten Bauteile in Schaltungen einzubauen. Sie können als Reihenschaltung oder auch Parallelschaltung eingesetzt werden. In diesem Artikel erklären wir dir diese zwei Arten der Schaltung, stellen alle wichtigen Formeln dazu auf und berechnen die Widerstände anschließend in einem Beispiel.
In unserem Video zeigen wir dir das alles so kurz und einfach wie möglich. Schau doch mal rein.
Inhaltsübersicht
Reihenschaltung Parallelschaltung einfach erklärt
Zuerst geben wir dir einen kurzen Überblick über die zwei Schaltungen. Bauteile, wie zum Beispiel der Widerstand oder der Kondensator, lassen sich unterschiedlich in einen Stromkreis einbauen. Einmal kann man sie zum Beispiel so einbauen, dass die Teile in Reihe, also hintereinander geschaltet sind. Das wäre dann die sogenannte Reihenschaltung. Ebenfalls kannst du die Bauteile so einbauen, dass sie im Stromkreis zueinander parallel sind, also sich gegenüber liegen. Das wäre die Parallelschaltung.
Der Strom und die Spannung verhält sich nun je nach Bauteil und Lage der anderen Teile unterschiedlich. Im Folgenden erklären wir dir die Verschiedenheiten.
Reihenschaltung
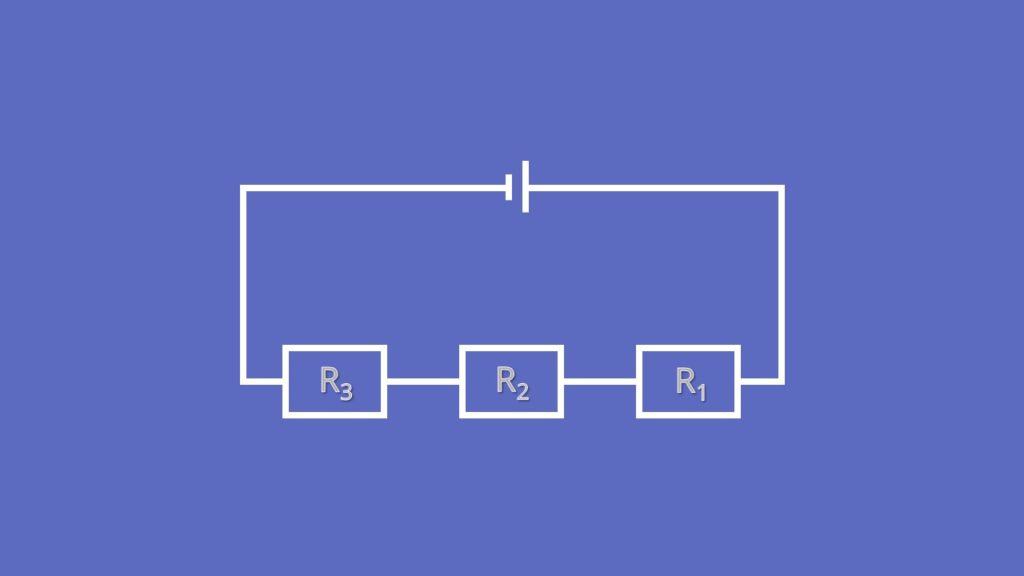
Beginnen wir mit der Reihenschaltung von Widerständen. Anschließend findest du noch eine kurze Erklärung zu der Reihenschaltung von Kondensatoren. Die Schaltung von Bauteilen in Reihe wird auch als Serienschaltung bezeichnet und sieht so aus:
Hier fließt der Strom zuerst durch den ersten Widerstand und von dort aus direkt zum nächsten und zu allen folgenden. Die Regeln zur Berechnung von Strom 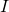 und Spannung
und Spannung 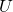 für die Widerstände
für die Widerstände 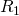 bis
bis 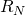 sehen so aus:
sehen so aus:
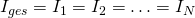
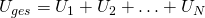
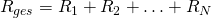
Der Strom bleibt hier also gleich, denn alle Elektronen, die durch den ersten Widerstand fließen, müssen auch durch den zweiten, dritten und alle folgenden Widerstände fließen. Die Ladung im Stromkreislauf mit Reihenschaltung verändert sich demnach nicht. Der Gesamtwiderstand einer Reihenschaltung ist die Summe aller einzelnen Widerstände. Das heißt: anstatt der vielen kleinen Widerstände könnte man auch einen großen Widerstand einbauen. Die Spannung ist proportional zum Widerstand, sonst wäre die Formel 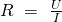 nicht erfüllt. Wir merken uns also:
nicht erfüllt. Wir merken uns also: 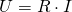 gilt auch hier. Das bedeutet für die Reihenschaltung je größer der Widerstand ist, desto mehr Spannung fällt an ihm ab.
gilt auch hier. Das bedeutet für die Reihenschaltung je größer der Widerstand ist, desto mehr Spannung fällt an ihm ab.
Reihenschaltung Kondensator
Sind die Bauteile in einem Stromkreis Kondensatoren statt Widerstände, so muss die Kapazität 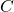 mit betrachtet werden. Falls du mehr zu dieser Kennzahl wissen möchtest, findest du hier
einen extra Beitrag dazu. Im Prinzip bleiben die oben festgestellten Gesetzmäßigkeiten gleich, nur die Zahlen lassen sich etwas anders ausdrücken.
mit betrachtet werden. Falls du mehr zu dieser Kennzahl wissen möchtest, findest du hier
einen extra Beitrag dazu. Im Prinzip bleiben die oben festgestellten Gesetzmäßigkeiten gleich, nur die Zahlen lassen sich etwas anders ausdrücken.
Zum Beispiel lässt sich die Spannung 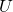 weiterhin über die einzelnen Teile der Kondensatoren
weiterhin über die einzelnen Teile der Kondensatoren 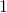 bis
bis 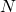 aufaddieren, sodass sich eine Gesamtspannung von
aufaddieren, sodass sich eine Gesamtspannung von 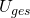 ergibt. Jedoch kann
ergibt. Jedoch kann 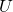 wie folgt ausgedrückt werden:
wie folgt ausgedrückt werden:
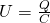
Dabei ist 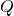 die Ladung. Eingesetzt ergibt das, die Gesamtspannung über alle Kondensatoren.
die Ladung. Eingesetzt ergibt das, die Gesamtspannung über alle Kondensatoren.
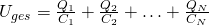
Der Strom ist an jedem Kondensator der gleiche. Zudem ergibt sich die Gesamtkapazität 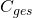 zu:
zu:
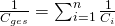
Parallelschaltung
Die zweite Möglichkeit Widerstände oder Kondensatoren zu verschalten, ist die Parallelschaltung. Die Bauteile sind hierbei parallel im Schaltkreis angeordnet. Das sieht dann so aus:
Bei jeder Abzweigung teilt sich der Stromfluss 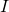 auf. Somit ergibt sich:
auf. Somit ergibt sich:
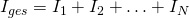
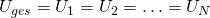
Für die Widerstände ergibt sich der Gesamtwiderstand 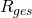 zu:
zu:
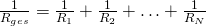
In der Parallelschaltung ist die Spannung konstant und die Stromstärke lässt sich durch die Aufteilung zu einer Gesamtstromstärke aufaddieren. Interessant ist, dass der Gesamtwiderstand in einer Parallelschaltung nicht größer wird, je mehr Widerstände parallel sind.
Der Grund ist der Folgende: Wenn wir uns den Widerstand wieder als Tür vorstellen, können mehr Menschen hindurchgehen je mehr Türen es nebeneinander gibt. Gleiches gilt auch für unsere Ladungsträger in der Parallelschaltung: Der Gesamtwiderstand wird also kleiner, je mehr Widerstände parallel sind!
Auch hier gilt natürlich die Formel 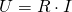 . Für den Spezialfall zweier paralleler Widerstände können wir die Formel für den Gesamtwiderstand umstellen und es gilt:
. Für den Spezialfall zweier paralleler Widerstände können wir die Formel für den Gesamtwiderstand umstellen und es gilt:
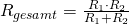
Parallelschaltung Kondensator
Werden Kondensatoren parallel zueinander geschalten, so ergibt sich die Gesamtkapazität 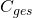 durch eine Addition der Kapazitäten der Kondensatoren
durch eine Addition der Kapazitäten der Kondensatoren 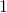 bis
bis 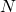 .
.
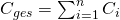
Widerstand berechnen – Beispiel
Schauen wir uns zum Abschluss noch eine Aufgabe an, damit wir sehen wie die Formeln für die Reihen– und Parallelschaltung bei Widerständen angewendet werden kann:
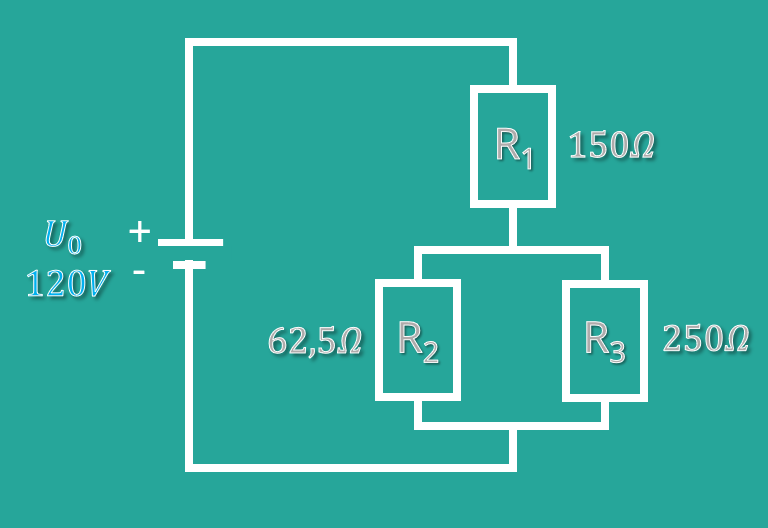
Gegeben ist folgende Schaltung mit den Daten:
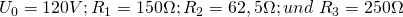
Gesucht sind somit:
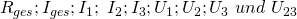
Zuerst berechnen wir den Gesamtwiderstand 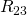 der Parallelschaltung:
der Parallelschaltung:
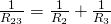
Wenn wir unsere Zahlen einsetzen, ergibt sich dann:
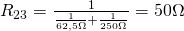
Daraus ermitteln wir dann den Gesamtwiderstand der Reihenschaltung:
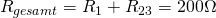
Nun können wir den Gesamtstrom dieser Reihenschaltung, der gleichzeitig ist, mit dem Ohmschen Gesetz berechnen:
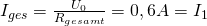
Jetzt können wir die Spannungen 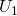 sowie
sowie 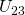 herausfinden:
herausfinden:
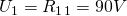
und aus 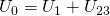 ergibt sich:
ergibt sich:
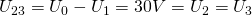
Zuletzt berechnen wir noch 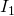 sowie
sowie 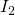 :
:
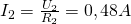
und