Video

Quiz

Hier geht's zum Video „Sinusfunktion“

Hier geht's zum Video „Elektrische Spannung“

Hier geht's zum Video „Stromstärke berechnen“

Hier geht's zum Video „Hydrostatischer Druck“

Phasenverschiebung

Wichtige Inhalte in diesem Video

Phasenverschiebung einfach erklärt

Phasenverschiebung berechnen

In diesem Beitrag beschäftigen wir uns mit der Phasenverschiebung. Wir erklären dir unter anderem was die Phasenverschiebung ist und wie du sie berechnen kannst.

Du lernst mit Videos besser? Perfekt! Auch zu diesem Thema haben wir ein animiertes Video , das du dir gerne ansehen kannst.

Inhaltsübersicht

Phasenverschiebung einfach erklärt

im Videozur Stelle im Video springen

Die Phase einer sinusförmigen Funktion $\sin(x)$ ist das Argument dieser Funktion. Für $\sin(x)$ ist das ; für $\sin(2\pi f t)$ ist das $2\pi f t$ .

Einfach gesagt gibt dir die Phasenverschiebung (auch Phasendifferenz oder Phasenlage) an, wie stark der erste Nulldurchgang einer beliebigen Sinusfunktion der Frequenz relativ zu einer nicht verschobenen Sinusfunktion derselben Frequenz nach links oder nach rechts verschoben ist.

In der Elektrotechnik führen Bauelemente wie Kondensatoren und Spulen dazu, dass zwischen Strom und Spannung eine Phasenverschiebung herrscht. Die Kenntnis der Phasenverschiebung spielt insbesondere bei der Betrachtung von Wechselstromkreisen eine zentrale Rolle.

Phasenverschiebung berechnen

im Videozur Stelle im Video springen

Dieser und der darauffolgende Abschnitt beantworten dir zwei Fragen

(1) was genau ist eine Phase und wie beeinflusst sie eine Sinusfunktion und

(2) wie lässt sich die Formel

$\Delta \varphi = 2\pi \cdot f \cdot \Delta t$ ,

um aus einer Zeitdifferenz die Phasenverschiebung zu berechnen, aufstellen?

Für die Antwort beschränken wir uns auf Sinusfunktionen. Die gleichen Argumente gelten aber auch für Cosinusfunktionen .

Sinusfunktionen und ihre Phasen

Jede physikalische Größe, sei es Strom , Spannung , Druck oder elektrische und magnetische Felder , die in ihren Werten periodisch auf und ab schwingt, lässt sich mit sinusförmigen Funktionen darstellen.

Diese sinusförmigen Funktionen besitzen dann folgende Form

$P(t) = P_0 \cdot \sin(2\pi f t + \varphi_P)$ .

Der Buchstabe steht hier repräsentativ für eine bestimmte physikalische Größe. Die Variable ist hier die Zeit , es könnte aber auch ein Ort oder eine Höhe sein.

Merke: Phase der Sinusfunktion

Das Argument, also das was in den Klammern der Sinusfunktion steht, wird als Phase (auch Phasenwinkel) $\varphi$ bezeichnet. Für die obige Sinusfunktion gilt

$\varphi = 2\pi f t + \varphi_P$ .

Der Buchstabe ist die Frequenz der Sinusfunktion und P_0 ist der Wert der physikalischen Größe, wenn der Sinus den Wert 1 annimmt ( P_0 wird auch als die Amplitude der Sinusfunktion bezeichnet).

Sinusfunktion, Amplitude, Wellenlänge, Phase — Phasenverschiebung: Illustration einer Sinusfunktion

Phasenverschiebung Definition

Es bleibt nun nur noch dieses ominöse $\varphi_P$ . Wäre das nicht vorhanden, dann wäre die Phase genau dann Null, wenn die Zeit Null ist und P(t) würde für t = 0 den Wert Null annehmen, da $\sin(0) = 0$ gilt.

Je nachdem welches Vorzeichen dieses $\varphi_P$ besitzt, wird die Phase zu einem früheren (für ein positives $\varphi_P$ ) oder zu einem späteren (für ein negatives $\varphi_P$ ) Zeitpunkt Null. Dieses $\varphi_P$ scheint also irgendwie den Zeitpunkt zu verschieben, zu dem die Phase (oder äquivalent die Sinusfunktion) Null wird.

Definition: Phasenverschiebung (Phasendifferenz, Phasenlage)

Die Phasenverschiebung (auch Phasendifferenz oder Phasenlage) $\varphi_P$ ist ein Maß dafür, wie weit der erste Nulldurchgang der Sinusfunktion nach links oder nach rechts verschoben wird.

Da die Sinusfunktion eine zusammenhängende, periodische Funktion ist, wird tatsächlich nicht nur der erste Nulldurchgang verschoben, sondern alle Punkte entlang der Sinuskurve.

Der Index beim Symbol $\varphi_P$ soll dich daran erinnern, dass $\varphi_P$ die Phasenverschiebung ist, die zu der physikalischen Größe gehört.

Phasenverschiebung, verschobene Sinusfunktion — Nicht verschobene (rot) und verschobene (blau) Sinusfunktion.

Horizontales Verschieben von Funktionen

Stelle dir eine Funktion f(t) vor, die dir zu jedem Zeitpunkt angibt, auf welcher Treppenstufe du gerade stehst.

Wenn du dir also einen beliebigen Zeitpunkt aussuchst, sagen wir gleich 5 Sekunden, und diesen in die Funktion einsetzt, bekommst du die Treppenstufe, sagen wir die fünfte Stufe.

Addition einer positiven Zahl

Jetzt addieren wir zum Argument der Funktion eine Zahl, beispielsweise 2 Sekunden. Die Funktion lautet dann f(t + 2) . Für die unveränderte Funktion hast du 5 Sekunden einsetzen müssen, um zur fünften Stufe zu gelangen. Für die veränderte Funktion musst du nun gleich 3 Sekunden einsetzen, also einen früheren Zeitpunkt.

Das gilt aber nicht nur für die fünfte Stufe, sondern für alle Stufen, die die Funktion darstellt. Würden wir die Funktion zeichnen, dann führt die Addition der 2 Sekunden dazu, dass die Zeitpunkte, zu denen du dich auf einer bestimmten Stufe befindest, früher stattfinden. Mit anderen Worten: Die Funktion als Ganzes wurde durch die Addition einer positiven Zahl zum Argument nach links verschoben.

Für die Addition einer negativen Zahl führt eine ähnliche Argumentation zum folgenden Ergebnis: Die Funktion als Ganzes wird durch die Addition einer negativen Zahl zum Argument nach rechts verschoben.

Und das gilt nicht nur für diese beispielhafte Treppenfunktion, sondern für jede Funktion, die du dir aussuchst. Also auch für die sinusförmigen Funktionen, die wir bisher betrachtet haben.

Horizontale Verschiebung von Funktionen, Treppenfunktion verschoben, Phasenverschiebung — Verschieben einer beispielshaften Treppenfunktion illustriert.

Phasenverschiebung Formel

In diesem Abschnitt schauen wir uns an, wie du die Phasenverschiebung berechnen kannst.

Gradmaß und Bogenmaß

Du wirst wahrscheinlich mit dem Gradmaß vertraut sein. Wenn du einen Kreis zeichnest, dann beginnst du bei 0°, führst deinen Stift weiter zu 90°, dann 180°, 270° und zum Schluss gelangst du bei 360° zum Startpunkt zurück.

Viel häufiger wird nicht das Gradmaß, sondern das Bogenmaß verwendet. Du kannst aber leicht zwischen diesen beiden Einheiten umrechnen.

Merke: Umrechnung Gradmaß/Bogenmaß

Die Umrechung zwischen Gradmaß und Bogenmaß basiert auf folgende Beziehung

$1 \ \pi = 180$ °.

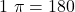Möchtest beispielsweise wissen, wie ein Winkel von ° in Bogenmaß lautet, dann rechnest du

$x_{\mathsf{RAD}} =\frac{x_{\mathsf{DEG}}}{180^{\circ}} \cdot \pi$ .

Formel

Wenn du eine physikalische Größe als Funktion der Zeit beschreibst, dann bedeutet das unter anderem zwei Sachen

(1) Du verwendest als Input für die Funktion die Zeit und

(2) zum Zeichnen der Funktion verwendest du als eine der Achsen die Zeit .

Du kannst aber in eine Sinusfunktion nicht einfach einsetzen, sondern musst es in ein Winkel umwandeln. Und genau das passiert, wenn du $2\pi f t$ berechnest.

Um mit dieser Information nun die Phasenverschiebung für eine gegebene Sinusfunktion zu berechnen, kannst du folgendermaßen vorgehen:

Schritt 1: Du zeichnest die gegebene Sinusfunktion.

Schritt 2: Du zeichnest dazu eine nicht verschobene Sinusfunktion mit derselben Frequenz.

Schritt 3: Du bestimmst die Zeitdifferenz $\Delta t$ zwischen diesen beiden Funktionen für den ersten Nulldurchgang.

Schritt 4: Diese Zeitdifferenz wandelst du mit $2\pi f \Delta t$ in eine Winkeldifferenz um. Diese Winkeldifferenz ist die gesuchte Phasenverschiebung (oder Phasendifferenz) $\Delta \varphi = 2\pi \cdot f \cdot \Delta t$ (auf das richtige Vorzeichen achten).

Im dritten Schritt kannst du auch die Zeitdifferenz zwischen den ersten beiden Maxima oder Minima verwenden.

Phasenverschiebung Beispielrechnung

Schauen wir uns ein Beispiel an. Nehmen wir dazu an, dass wir folgende verschobene Sinusfunktion haben.

Phasenverschiebung berechnen — Phasenverschiebung berechnen: Verschobene Sinusfunktion.

Die Frequenz beträgt 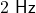$2 \ \mathsf{Hz}$ und die Amplitude ist 1. Damit ist der erste Schritt bereits erledigt.

Im zweiten Schritt zeichnen wir eine nicht verschobene Sinusfunktion mit derselben Frequenz ein.

Phasenverschiebung berechnen — Phasenverschiebung berechnen: Verschobene (blau) und nicht verschobene (rot) Sinusfunktion.

Jetzt haben wir beide Funktionen in einem Diagramm. Für jede Funktion suchen wir den Zeitpunkt des ersten Nulldurchgangs. Bei der nicht verschobenen Sinusfunktion ist das gerade $t = 0 \ \mathsf{s}$ . Für die verschobene Sinusfunktion erhalten wir $t = 2 \ \mathsf{s}$ .

Im letzten Schritt verwenden wir die Formel und erhalten für die Phasenverschiebung

$\Delta \varphi = 2\pi \cdot f \cdot \Delta t = 2\pi \cdot 2 \ \mathsf{\frac{1}{s}} \cdot (2 \ \mathsf{s} - 0 \ \mathsf{s}) = 8\pi$ .

Die Funktion ist nach rechts verschoben. Damit bekommt die berechnete Phasenverschiebung ein Minuszeichen.

Hinweis: In diesem Beispiel und auch bei der Beschreibung der Formel gehen wir davon aus, dass wir uns für die Phasenverschiebung einer verschobenen Sinusfunktion relativ zu einer nicht verschobenen Sinusfunktion interessieren. Du kannst aber mit denselben Schritten die Phasenverschiebung zwischen zwei verschobenen Sinusfunktionen bestimmen. Beachte auch, dass du für beide Funktionen denselben ersten Nulldurchgang wählst. Im Bild oben ist der „wahre“ erste Nulldurchgang der verschobenen Funktion als orangener Punkt dargestellt. Der dazugehörige Nulldurchgang der nicht verschobenen Funktion ist der andere orangene Punkt weiter links.

Phasenverschiebung Elektrotechnik

In diesem Abschnitt schauen wir uns kurz an, wie die gängigen Bauelemente Widerstand, Kondensator und Spule die Phasenverschiebung zwischen Strom und Spannung beeinflussen.

Phasenverschiebung Widerstand

Ein ohmscher Widerstand führt zu keiner Phasenverschiebung zwischen Strom und Spannung. Das folgt direkt aus dem ohmschen Gesetz

$U = R \cdot I$ .

Wenn sich die zeitliche Änderung der Stromstärke wie eine Sinusfunktion verhält, so tut das auch die Spannung.

Phasenverschiebung Kondensator

Beim Kondensator wird die Phase der Stromstärke relativ zur Spannung nach links verschoben. Die Phasendifferenz zwischen Stromstärke und Spannung ist daher positiv. In einfachen Worten ausgedrückt, eilt die Stromstärke der Spannung um 90° vor.

Diese Beobachtung folgt aus der Kondensatorgleichung

$I = C \cdot \frac{\mathsf{d}U}{\mathsf{dt}}$ ,

wobei die Kapazität des Kondensators ist.

Wenn sich die zeitliche Änderung der Spannung wie eine Sinusfunktion verhält, so ist die zeitliche Änderung der Stromstärke eine Cosinusfunktion.

Stromstärke eilt vor Spannung, Phasenverschiebung Kondensator — Phasenverschiebung: Stromstärke eilt vor Spannung um 90°.

Phasenverschiebung Spule

Bei der Spule wird die Phase der Stromstärke relativ zur Spannung nach rechts verschoben. Die Phasendifferenz zwischen Stromstärke und Spannung ist daher negativ. In einfachen Worten ausgedrückt, eilt die Spannung der Stromstärke um 90° vor.

Diese Beobachtung folgt aus der Spulengleichung

$U = L \cdot \frac{\mathsf{d}I}{\mathsf{dt}}$ ,

wobei die Induktivität der Spule ist.

Wenn sich die zeitliche Änderung der Stromstärke wie eine Sinusfunktion verhält, so ist die zeitliche Änderung der Spannung eine Cosinusfunktion.

Phasenverschiebung Spule, Spannung eilt vor Stromstärke — Phasenverschiebung Spule: Spannung eilt vor Stromstärke um 90°.

zur Videoseite: Phasenverschiebung

Beliebte Inhalte aus dem Bereich Elektrotechnik Grundlagen

Scheinleistung, Blindleistung, Wirkleistung

Phasenverschiebung

Hallo, leider nutzt du einen AdBlocker.

Auf Studyflix bieten wir dir kostenlos hochwertige Bildung an. Dies können wir nur durch die Unterstützung unserer Werbepartner tun.

Schalte bitte deinen Adblocker für Studyflix aus oder füge uns zu deinen Ausnahmen hinzu. Das tut dir nicht weh und hilft uns weiter.

Danke!
Dein Studyflix-Team

Wenn du nicht weißt, wie du deinen Adblocker deaktivierst oder Studyflix zu den Ausnahmen hinzufügst, findest du hier eine kurze Anleitung. Bitte .