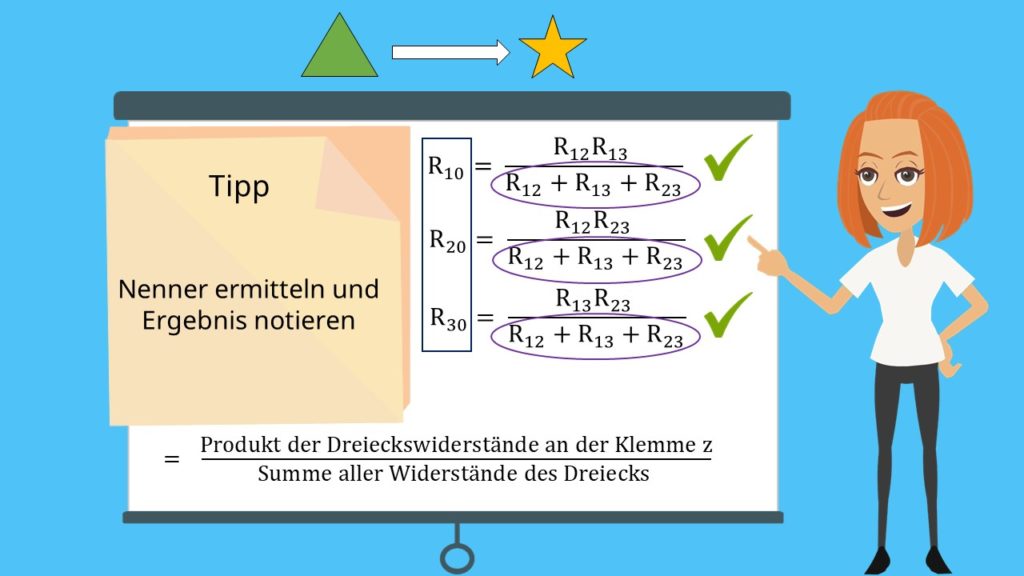
Stern-Dreieck-Umwandlung
Du kennst zwar den Unterscheid zwischen der Stern- und Dreieckschaltung, möchtest jetzt allerdings noch wissen, wie die Stern-Dreieck-Umwandlung funktioniert? Wir erklären dir, wie man die Stern- oder Dreieckschaltung in die jeweils andere Schaltung umwandelt an einem einfachen Beispiel.
Schau auch gerne in unser Video dazu rein. Dort ist alles in kürzester Zeit erklärt.
Inhaltsübersicht
Stern Dreieck Umwandlung einfach erklärt
Die Stern Dreieck Umwandlung kann dir dabei helfen komplexe Widerstandsschaltungen zu vereinfachen und sie in Reihen -und Parallelschaltungen zu überführen. Wir zeigen dir im Folgenden die theoretischen Grundlagen zu den Umwandlungen. Wichtig sind dabei besonders die Formeln.
Für die Umwandlung von der Stern in die Dreiecksschaltung lauten sie:



Die Umwandlung von der Dreiecks in die Sternschaltung erfolgt über:



Stern-Dreieck-Umwandlung Herleitung
Die Stern-Dreieck-Umwandlung wird auch häufig als Delta-Star-Transformation oder Kennelly-Theorem bezeichnet. Um die eine Schaltung in die andere umzuwandeln, muss uns erst klar werden, was das elektrotechnisch bedeutet. Damit die Schaltungen gleichwertig sind, musst du zwischen zwei Klemmen immer den gleichen Widerstandswert haben.
Misst du zwischen den Punkten 1 und 2 deiner vorhandenen Stern- oder Dreieckschaltung einen gewissen Widerstand, beispielsweise 25 Ohm, so musst du in der transformierten Stern- bzw. Dreieckschaltung ebenfalls zwischen den Punkten 1 und 2 diesen Widerstandswert messen. Dieses Wissen ist die Grundlage für die Berechnung zur Umwandlung zwischen den Schaltungen.
Betrachten wir beispielhaft die Klemmen 1 und 2 für die Herleitung:
In der Sternschaltung befinden sich die Widerstände 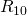 und
und  , welche über den Sternpunkt zwischen den Punkten 1 und 2 verbunden sind. Der Widerstand
, welche über den Sternpunkt zwischen den Punkten 1 und 2 verbunden sind. Der Widerstand  trägt zu unserer Berechnung nichts bei, weil er von unserer Betrachtung aus „in der Luft“ hängt, also keine elektrische Verbindung mit den Punkten 1 und 2 hat. Daher kannst du ihn vernachlässigen.
trägt zu unserer Berechnung nichts bei, weil er von unserer Betrachtung aus „in der Luft“ hängt, also keine elektrische Verbindung mit den Punkten 1 und 2 hat. Daher kannst du ihn vernachlässigen.
Lass uns jetzt einen Blick auf die Dreieckschaltung werfen. Hier ist der Widerstand  direkt zwischen den Punkten 1 und 2 und parallel dazu die Widerstände
direkt zwischen den Punkten 1 und 2 und parallel dazu die Widerstände  und
und  , die über den Punkt 3 verbunden sind. Wichtig ist hier, dass du die Parallelschaltung nicht vergisst, denn es besteht über die Klemme 3 und den zwei Widerständen eine elektrische Verbindung zwischen den Punkten 1 und 2. Es muss also gelten:
, die über den Punkt 3 verbunden sind. Wichtig ist hier, dass du die Parallelschaltung nicht vergisst, denn es besteht über die Klemme 3 und den zwei Widerständen eine elektrische Verbindung zwischen den Punkten 1 und 2. Es muss also gelten: 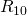 in Reihe zu
in Reihe zu  ist gleich parallel zur (Reihenschaltung aus
ist gleich parallel zur (Reihenschaltung aus  und
und  ). Analog ergibt sich für die anderen Klemmenpaare:
). Analog ergibt sich für die anderen Klemmenpaare:


Jetzt haben wir drei Gleichungen und die drei Unbekannten  ,
,  und
und  oder
oder 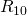 ,
,  und
und  und können dieses Gleichungssystem dementsprechend lösen, je nachdem ob wir vom Stern ins Dreieck oder umgekehrt umrechnen möchten. In den folgenden Absätzen präsentieren wir dir die sich daraus ergebenden Formeln für die Umwandlung einer Stern in eine Dreieckschaltung und umgekehrt.
und können dieses Gleichungssystem dementsprechend lösen, je nachdem ob wir vom Stern ins Dreieck oder umgekehrt umrechnen möchten. In den folgenden Absätzen präsentieren wir dir die sich daraus ergebenden Formeln für die Umwandlung einer Stern in eine Dreieckschaltung und umgekehrt.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Stern Dreieck Umwandlung Formel
Für die Umwandlung einer Sternschaltung in eine Dreieckschaltung bekommen wir also folgende Formeln für die Dreieckswiderstände:



Du siehst, wenn du eine Sternschaltung in eine Dreieckschaltung umwandeln möchtest, musst du die bekannten Werte der Sternwiderstände in die drei Formeln einsetzen. Zunächst multiplizierst du alle drei Widerstände miteinander und addierst die drei entstandenen Produkte. Dies ist der Zähler deines Bruches. Im Nenner steht immer der Widerstand, der nicht an den zwei Klemmen angeschlossen ist, zwischen denen du den Dreieckswiderstand berechnest. Beim Rechnen selbst ist es für dich einfacher zuerst den Zähler zu ermitteln und dir das Ergebnis zu notieren. Diesen Wert kannst du dann für alle drei Berechnungen im Zähler einsetzen, da sich dieser nicht ändert.
Dreieck Stern Umwandlung Formel
Nun wollen wir uns anschauen, wie Du vorgehen musst, wenn du eine Dreieckschaltung in eine Sternschaltung umwandeln willst. Für die Umrechnung stehen dir folgende Gleichungen zur Verfügung:



Nun sind dir die Werte der Widerstände in der Dreieckschaltung bekannt und du möchtest die Werte der Sternwiderstände berechnen. Unser Nenner ist immer die Summe aus allen drei Widerständen der Dreieckschaltung und im Zähler steht das Produkt aus den beiden Widerständen, die an der Klemme hängen, für die du gerade den Sternwiderstand ausrechnest. Es bietet sich für all deine Berechnungen an, zunächst den Nenner auszurechnen und zu notieren, da dieser immer gleich ist.
Umwandlung bei drei gleich großen Widerständen
Für den Sonderfall, dass die drei Widerstände in deiner Stern- oder Dreieckschaltung den gleichen Wert haben, vereinfacht sich die Berechnung für dich. Die Umrechnung erfolgt mit den Formeln:

Der Dreieckswiderstand ist also dreimal so groß wie der Sternwiderstand bzw. hat der Sternwiderstand nur ein Drittel des Werts des Dreieckwiderstands.
Stern-Dreieck-Umwandlung Beispiel
Schauen wir uns nun die Umwandlungen an einfachen Beispielen an. In unserem Beispiel wollen wir den Ersatzwiderstand einer Brückenschaltung berechnen, die mit folgenden Widerständen besetzt ist und so aussieht:
Da wir hier keine Reihen- bzw. Parallelschaltung haben, ist es für uns unmöglich den Ersatzwiderstand mit einfachen Mitteln zu berechnen. Wir müssen unsere Schaltung also so verändern, dass wir am Schluss nur noch parallel und in Reihe geschaltete Widerstände haben. Und hier kommt jetzt unsere Stern- und Dreieckschaltung ins Spiel bzw. deren Transformationen. Um die Umwandlung in beide Richtungen, also von Stern in Dreieck und von Dreieck in Stern zu zeigen, werden wir das Beispiel auf beide Arten rechnen.
Umwandlung Sternschaltung in Dreieckschaltung
Fangen wir zunächst mit der Stern-zu-Dreieck-Transformation an. Durch diese Transformation bekommen wir eine reine Parallel- und Reihenschaltung der Widerstände, mit der wir ganz einfach den Ersatzwiderstand berechnen können. Als erstes suchen wir uns die Sternschaltung mit  ,
,  und
und  aus und beschriften deren Klemmen mit 1, 2 und 3. Im zweiten Schritt tauschen wir die Sternschaltung durch eine Dreieckschaltung aus. Dazu entfernen wir einfach die Widerstände
aus und beschriften deren Klemmen mit 1, 2 und 3. Im zweiten Schritt tauschen wir die Sternschaltung durch eine Dreieckschaltung aus. Dazu entfernen wir einfach die Widerstände  ,
,  und
und  aus der Schaltung.
aus der Schaltung.
Zurück bleiben der  und der
und der  und unsere drei eingezeichneten Klemmpunkte. Zwischen diesen zeichnen wir nun drei neue Widerstände als Dreieckschaltung und benennen sie anhand der Klemmen, zwischen denen sie angeschlossen sind. Die Widerstände müssen jetzt auf jeden Fall anders heißen, da sie auch andere Werte haben. Beschrifte sie am besten nach dem simplen Zahlenschema, bei dem die Indizes den Klemmennummern entsprechen. Für den Fall, dass du die entstandene Reihen- und Parallelschaltung nicht auf Anhieb siehst, haben wir die Schaltung noch einmal umgezeichnet.
und unsere drei eingezeichneten Klemmpunkte. Zwischen diesen zeichnen wir nun drei neue Widerstände als Dreieckschaltung und benennen sie anhand der Klemmen, zwischen denen sie angeschlossen sind. Die Widerstände müssen jetzt auf jeden Fall anders heißen, da sie auch andere Werte haben. Beschrifte sie am besten nach dem simplen Zahlenschema, bei dem die Indizes den Klemmennummern entsprechen. Für den Fall, dass du die entstandene Reihen- und Parallelschaltung nicht auf Anhieb siehst, haben wir die Schaltung noch einmal umgezeichnet.
Nun geht es an die Berechnung der Werte für  ,
,  und
und  . Solltest du Dir schwer tun die Widerstände R1, R3 und R5 in die Formeln einzutragen, notiere dir die Beschreibungen mit den Klemmen daneben, also
. Solltest du Dir schwer tun die Widerstände R1, R3 und R5 in die Formeln einzutragen, notiere dir die Beschreibungen mit den Klemmen daneben, also 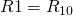 ,
,  und
und  . In unserer Berechnung wollen wir die echten Bezeichnungen der Widerstände benutzen. Als Erstes rechnen wir den Zähler Z aus, der bei einer Stern-zu-Dreieck-Umwandlung immer der gleiche ist:
. In unserer Berechnung wollen wir die echten Bezeichnungen der Widerstände benutzen. Als Erstes rechnen wir den Zähler Z aus, der bei einer Stern-zu-Dreieck-Umwandlung immer der gleiche ist:
Damit können wir nun die ganz einfach ausrechnen. Diese Werte setzen wir nun in unser Bild mit der reinen Reihen- und Parallelschaltung ein und können so bequem den Ersatzwiderstand von 6,24 Ω ausrechnen.
Umwandlung Dreieckschaltung in Sternschaltung
Jetzt wollen wir die gleiche Schaltung rechnen, aber diesmal wandeln wir eine Dreieckschaltung in eine Sternschaltung um, damit du siehst, dass am Schluss der gleiche Wert für den Ersatzwiderstand herauskommt.
Auch hier suchen wir uns zunächst die Dreieckschaltung mit  ,
,  und
und  aus und beschriften die drei Klemmpunkte mit 1, 2 und 3. Dann entfernen wir die Widerstände der Dreieckschaltung. Übrig bleiben der
aus und beschriften die drei Klemmpunkte mit 1, 2 und 3. Dann entfernen wir die Widerstände der Dreieckschaltung. Übrig bleiben der  und der
und der  , sowie unsere drei Klemmpunkte. Zwischen den Klemmen zeichnen wir nun eine Sternschaltung und bezeichnen die Widerstände anhand der Klemmen, über die sie mit dem Sternpunkt verbunden sind. Durch diese Umformung entsteht nun eine Schaltung, die nur aus Reihen- und Parallelschaltung besteht und von der du ganz einfach den Ersatzwiderstand ausrechnen kannst. Die Schaltung kann nur vereinfacht durch die nebenstehende Schaltung dargestellt werden.
, sowie unsere drei Klemmpunkte. Zwischen den Klemmen zeichnen wir nun eine Sternschaltung und bezeichnen die Widerstände anhand der Klemmen, über die sie mit dem Sternpunkt verbunden sind. Durch diese Umformung entsteht nun eine Schaltung, die nur aus Reihen- und Parallelschaltung besteht und von der du ganz einfach den Ersatzwiderstand ausrechnen kannst. Die Schaltung kann nur vereinfacht durch die nebenstehende Schaltung dargestellt werden.
Nun wollen wir die Werte für 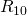 ,
,  und
und  berechnen. Wie bei der vorherigen Aufgabe, gilt auch hier: Tust du dir schwer beim Einsetzen der realen Widerstandsbezeichnungen in die Formeln, schreibe dir als Hilfe die Standardnamen der Dreieckschaltung daneben:
berechnen. Wie bei der vorherigen Aufgabe, gilt auch hier: Tust du dir schwer beim Einsetzen der realen Widerstandsbezeichnungen in die Formeln, schreibe dir als Hilfe die Standardnamen der Dreieckschaltung daneben:  ,
,  und
und  . Wir verwenden wieder die realen Bezeichnungen.
. Wir verwenden wieder die realen Bezeichnungen.
Als Erstes berechnen wir die Summe der Dreieckswiderstände für unseren Nenner N. Nun können wir die Sternwiderstände ausrechnen: Diese Werte setzen wir nun in unser Ersatzschaltbild und können so durch zusammenfassen der Widerstände den Ersatzwiderstand von 6,24 Ω ausrechnen. Es kommt das gleiche heraus wie bei der Stern-zu-Dreieck-Transformation und das muss auch so sein, denn es ist ja die gleiche Schaltung.