Brückenschaltung
In diesem Beitrag erklären wir dir die wichtigsten Formeln und Berechnungen zur Brückenschaltung und worum es sich bei einer Wheatstone Brücke handelt.
Alles auf einen Blick findest du auch in unserem Video .
Inhaltsübersicht
Brückenschaltung einfach erklärt
Bei Brückenschaltungen handelt es sich um eine bestimmte Verschaltung von elektronischen Bauelementen. Am häufigsten wird dir die Wheatstone-Brücke begegnen. In diesem Artikel wird daher Wheatstone-Brücke und Brückenschaltung synonym verwendet.
Bei einer Wheatstone-Brücke handelt es sich um eine Schaltung von vier Widerständen. Sie findet in der Regel in Kombination mit Sensoren Verwendung, um von einer Spannungsänderung auf die Änderung einer physikalischen Größe (Temperatur, Dehnung, Druck etc.) zu schließen.
Brückenschaltung Aufbau: Wheatstone-Brücke
Eine Wheatstone-Brücke besteht im einfachsten Fall aus vier Widerständen die nach folgendem Schema verschalten sind.
Es handelt sich dabei also, um zwei parallele Reihenschaltungen mit je zwei Widerständen.
Die Brückenschaltung wird an ihrem Eingang von einer Spannungsquelle, in diesem Fall,  gespeist. Die Ausgangsspannung
gespeist. Die Ausgangsspannung  wird zwischen den Widerständen gemessen.
wird zwischen den Widerständen gemessen.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Brückenschaltung Formel
Bei den Berechnungen zur Wheatstone-Brücke ist häufig der abgeglichene Fall relevant. Von einer abgeglichenen Brücke wird gesprochen, wenn die Widerstandswerte so gewählt sind, dass die Ausgangsspannung  0V beträgt.
0V beträgt.
Dies ist dann der Fall wenn für das Verhältnis der Widerstände  und
und  gilt:
gilt:

Befindet sich für den abgeglichenen Fall ein Widerstand  zwischen den Ausgangsklemmen, so kann dieser ignoriert werden, da die an ihm abfallende Spannung
zwischen den Ausgangsklemmen, so kann dieser ignoriert werden, da die an ihm abfallende Spannung 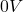 beträgt und demzufolge auch kein Strom durch ihn fließt.
beträgt und demzufolge auch kein Strom durch ihn fließt.
Brückenschaltung berechnen
Dieser Zusammenhang kann folgendermaßen hergeleitet werden:
Die Spannung  entspricht der Spannungdifferenz von
entspricht der Spannungdifferenz von  und
und  :
:

Für den abgeglichenen Fall gilt:

Damit ergibt sich:


An dieser Stelle können die Spannungen  und
und  über den Spannungsteiler berechnet werden.
über den Spannungsteiler berechnet werden.
Für  gilt:
gilt:

Für  gilt:
gilt:

Eingesetzt in die obige Formel ergibt sich:

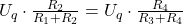
Nachdem beide Seiten durch  dividiert werden:
dividiert werden:

Nun kann auf beiden Seiten der Kehrbruch gebildet werden:

Anschließend werden die Brüche aufgeteilt:


Nach Subtraktion von  ergibt sich die Formel für die abgeglichene Brückenschaltung:
ergibt sich die Formel für die abgeglichene Brückenschaltung:

Unabgeglichene Brückenschaltung
Bei der unabgeglichenen Brückenschaltung ist das Verhältnis der Widerstände so, dass die Ausgangsspannung  nicht
nicht 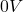 beträgt.
beträgt.


Um für diesen Fall die Ausgangsspannung  zu bestimmen, müssen zunächst die Spannungen
zu bestimmen, müssen zunächst die Spannungen  und
und  bestimmt werden und anschließend ihre Differenz ermittelt werden.
bestimmt werden und anschließend ihre Differenz ermittelt werden.
Für die Ausgangsspannung gilt:

Für die Teilspannungen  und
und  ergibt sich:
ergibt sich:


Befindet sich für den unabgeglichenen Fall ein Widerstand  an den Ausgangsklemmen, so kann dieser nicht ignoriert werden. Da eine eine solche Brückenschaltung nicht durch Reihen oder Parallelschaltungen beschrieben werden kann, ist es notwendig sie mittels Dreieck-Stern Umwandlung so zu transformieren, dass sie durch Reihen und Parallelschaltungen Beschrieben werden kann.
an den Ausgangsklemmen, so kann dieser nicht ignoriert werden. Da eine eine solche Brückenschaltung nicht durch Reihen oder Parallelschaltungen beschrieben werden kann, ist es notwendig sie mittels Dreieck-Stern Umwandlung so zu transformieren, dass sie durch Reihen und Parallelschaltungen Beschrieben werden kann.
Brückenschaltung Beispiel: Wheatstone-Brücke mit Temperatursensor
Im Folgenden schauen wir uns noch ein Beispiel für eine Brückenschaltung an.
Dabei ist eine Brückenschaltung mit den drei Widerständen  und
und  und einem PT100 Temperatursensor gegeben. Ein PT100 Sensor ändert seinen Widerstandwert je nachdem welche Temperatur er aufweist. Bei einer Temperatur von 0°C beträgt er
und einem PT100 Temperatursensor gegeben. Ein PT100 Sensor ändert seinen Widerstandwert je nachdem welche Temperatur er aufweist. Bei einer Temperatur von 0°C beträgt er  . Für die Widerstände gilt
. Für die Widerstände gilt  und
und  . Die Betriebsspannung
. Die Betriebsspannung  beträgt
beträgt  .
.
Weitere Widerstandwerte des PT100 kannst du entweder berechnen oder aus einer Tabelle im Internet raussuchen. Für eine Temperatur von 25°C kann so ein Widerstandswert von  ermittelt werden.
ermittelt werden.
Zuerst soll nun der Widerstand  so gewählt werden, dass die Brücke bei einer Temperatur von 0°C angepasst ist.
so gewählt werden, dass die Brücke bei einer Temperatur von 0°C angepasst ist.
Anschließend soll die Ausgangsspannung der Brücke bei einer Temperatur von 25°C berechnet werden.
Für eine angepasste Brückenschaltung gilt:

Umgestellt nach  ergibt sich:
ergibt sich:
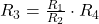
In unserem Fall handelt es sich bei  , um den PT100 Temperatursensor mit dem Widerstand
, um den PT100 Temperatursensor mit dem Widerstand  .
.

Da hier eine Abgleichung bei 0°C erwünscht ist, setzen wir für  den Wert ein, den der Sensor bei 0°C aufweist. In diesem Fall also
den Wert ein, den der Sensor bei 0°C aufweist. In diesem Fall also 


An dieser Stelle sind alle Widerstandswerte der Brücke bekannt, nun kann die Ausgangsspannung für eine Temperatur von 25°C berechnet werden. Wichtig ist, dass für eine Temperatur von 25°C die Brücke nicht länger abgeglichen ist und daher die Abgleichsbedingung nicht länger gilt. Die Ausgangsspannung wird in diesem Fall also ungleich 0 ein.
Für die Ausgangsspannung gilt:

Unter Anwendung des Spannungsteilers für  und
und  ergibt sich:
ergibt sich:


Daraus folgt:

Nach Einsetzen der Betriebsspannung und der Widerstandswerte kann die Ausgangsspannung ermittelt werden:


Brückenschaltung — häufigste Fragen
(ausklappen)
Brückenschaltung — häufigste Fragen
(ausklappen)-
Wie berechne ich U_AB bei einer unabgeglichenen Wheatstone-Brücke, wenn kein Widerstand zwischen A und B hängt?Du berechnest
 als Differenz zweier unabhängiger Spannungsteiler:
als Differenz zweier unabhängiger Spannungsteiler:  . Ohne Widerstand zwischen A und B fließt kein Querstrom, daher beeinflussen sich die Zweige nicht. Konkret:
. Ohne Widerstand zwischen A und B fließt kein Querstrom, daher beeinflussen sich die Zweige nicht. Konkret:  und
und  .
.
-
Wie entscheide ich, ob ich bei einer Brückenschaltung Dreieck-Stern-Umwandlung brauche oder ob Spannungsteiler ausreichen?Spannungsteiler reichen, wenn A und B nicht leitend verbunden sind und nur hochohmig gemessen wird. Dann sind die beiden Seiten echte Reihenschaltungen gegen denselben Bezugspunkt. Eine Dreieck-Stern-Umwandlung oder Knotenanalyse brauchst du, sobald zwischen A und B eine Last liegt, weil dann ein Querstrom die Teilspannungen verändert.
-
Welche typischen Fehler passieren beim Einzeichnen von U_AB, weil ich A und B gegen den falschen Bezugspunkt messe?Ein typischer Fehler ist,
 mit zwei verschiedenen Bezugspunkten zu bilden, obwohl beide Spannungen gegen denselben Knoten gemessen werden müssen. Dann addierst oder subtrahierst du falsche Vorzeichen. Achte darauf:
mit zwei verschiedenen Bezugspunkten zu bilden, obwohl beide Spannungen gegen denselben Knoten gemessen werden müssen. Dann addierst oder subtrahierst du falsche Vorzeichen. Achte darauf:  gilt nur, wenn
gilt nur, wenn  und
und  beide gegen Masse beziehungsweise den Minuspol von
beide gegen Masse beziehungsweise den Minuspol von  definiert sind.
definiert sind.
-
Wie kann ich bei einer Sensor-Brücke grob abschätzen, wie stark sich U_AB bei einer kleinen Widerstandsänderung am Sensor ändert?Du schätzt die Änderung über die Steigung des Spannungsteilers ab, also näherungsweise
 . Für den Sensorzweig gilt
. Für den Sensorzweig gilt  , daher
, daher  . Bei Abgleich um
. Bei Abgleich um  wird die Näherung besonders einfach.
wird die Näherung besonders einfach.
Brückenschaltung und Stern- und Dreieckschaltung
Innerhalb der Brückenschaltung sind viele elektrische Bauelemente miteinander verschachtelt. Die Bauelemente sind unter anderem auch über Stern- und Dreickschaltungen verbunden. Bei der Sternschaltung hängen drei Widerstände an drei unterschiedlichen Punkten. Bei der Dreieckschaltung liegen drei Widerstände in zwischen drei Punkten.
Mehr über den detaillierten Aufbau der Stern- und Dreieckschaltung und auch wie sie bei Motoren verwendet wird, findest du in unserem zugehörigen Beitrag !


