Elektrische Leitfähigkeit
Warum leitet Kupfer den Strom besser als Wasser? Diese Frage stellst du dir nach diesem Artikel sicherlich nicht mehr! Wir behandeln im Folgenden die elektrische Leitfähigkeit und schauen uns unter anderem die Formeln an. Zum Schluss kannst du dann dein Wissen auch anhand von zwei Beispielen testen.
Du möchtest das Thema lieber visuell unterstützt erklärt bekommen? Dann schau dir auf jeden Fall unser Video zu diesem Artikel an.
Inhaltsübersicht
Elektrische Leitfähigkeit Formel
Für die elektrische Leitfähigkeit gibt es drei verschiedene Formelzeichen  (griechisch: Sigma),
(griechisch: Sigma),  (Kappa) und
(Kappa) und  (Gamma). Im Folgenden benutzen wir
(Gamma). Im Folgenden benutzen wir  . Die Formel der elektrische Leitfähigkeit,oder auch spezifische Leitwert genannt, wird beschrieben durch
. Die Formel der elektrische Leitfähigkeit,oder auch spezifische Leitwert genannt, wird beschrieben durch
 .
.
Dabei nennt man  (Rho) den spezifische Widerstand. Du kannst den Widerstand
(Rho) den spezifische Widerstand. Du kannst den Widerstand  eines Leiters mit seinen Parametern durch
eines Leiters mit seinen Parametern durch

beschreiben. Der Widerstand  ist also gleich dem spezifischen Widerstand
ist also gleich dem spezifischen Widerstand  mal der Länge des Leiters
mal der Länge des Leiters  durch die Querschnittsfläche
durch die Querschnittsfläche  . Wenn du nun diese Formel mithilfe des spezifischen Leitwerts
. Wenn du nun diese Formel mithilfe des spezifischen Leitwerts  ausdrücken willst, ist es hilfreich zu wissen, dass der Leitwert
ausdrücken willst, ist es hilfreich zu wissen, dass der Leitwert  eines Leiters durch
eines Leiters durch

beschrieben wird. Setzt man den spezifischen Leitwert  und den Leitwert
und den Leitwert  in die obere Formel ein, folgt
in die obere Formel ein, folgt
 .
.
Durch weiteres Umformen erhält man den Ausdruck
 .
.
Mithilfe der elektrischen Leitfähigkeit kann man auch den wichtigen Zusammenhang zwischen Stromdichte und elektrische Feldstärke mit

beschreiben. Wenn du mehr über Stromdichte und elektrische Feldstärke erfahren willst, kannst du gerne unsere Videos zu den Themen anschauen.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Elektrische Leitfähigkeit Einheit
Die Einheit der elektrischen Leitfähigkeit  ist
ist
![Rendered by QuickLaTeX.com [\sigma] = \mathrm{1\frac{S}{m}}](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-c22d1b6f6814dfaaaf96d0b8b30ffb17_l3.png) (Siemens pro Meter).
(Siemens pro Meter).
Diese Einheiten leiten sich aus der Formel  ab. Wenn man diese Formel nach
ab. Wenn man diese Formel nach  auflöst, erhält man
auflöst, erhält man
 .
.
Vom Leitwert  ist die Maßeinheit als
ist die Maßeinheit als
![Rendered by QuickLaTeX.com [G] = \mathrm{\frac{1}{\Omega} = 1S}](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-8f37badc6d8cf5d40571598f8e9336c6_l3.png) (Siemens)
(Siemens)
definiert. Setzt du nun alle Einheiten in die Formel ein erhältst du
![Rendered by QuickLaTeX.com [\sigma] = \mathrm{1S \cdot 1\frac{m}{m^2} = 1\frac{S}{m}}](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-29ea8a848331eaaabd329a3f62df1759_l3.png) .
.
Du wirst auch öfter die Einheiten  ,
,  oder
oder  sehen. Die einzelnen Messgrößen kannst du durch
sehen. Die einzelnen Messgrößen kannst du durch  und durch
und durch  umrechnen.
umrechnen.
Elektrische Leitfähigkeit von Metallen
Je nachdem, wie viele frei bewegliche Elektronen verfügbar sind, leitet ein Material besser als das andere. Prinzipiell ist jedes Material leitend, jedoch ist beispielsweise bei Isolatoren der fließende Strom vernachlässigbar gering, weshalb man hier von Nichtleitern spricht.
Bei Metallbindungen sind die Valenzelektronen, also die äußersten Elektronen im Atom, frei beweglich. Diese befinden sich im sogenannten Leitungsband. Wenn du mehr darüber wissen möchtest, dann schaue dir unser Video zur Fermi Energie an. Die Elektronen bilden dort das sogenannte Elektronengas. Metalle leiten dementsprechend vergleichsweise gut. Wenn du nun eine Spannung an ein Metall anlegst, dann bewegen sich die Valenzelektronen langsam zum Pluspol hin, da sie von diesem angezogen werden.
In diesem Bild siehst du, dass manche Elektronen nicht direkt Richtung Pluspol gezogen werden können, da sozusagen der feste Atomkern im Weg ist. Diese werden dort abgebremst und etwas umgelenkt. Deshalb können Elektronen im Metall nicht unendlich lang beschleunigt werden und so entsteht der spezifische Widerstand beziehungsweise die elektrische Leitfähigkeit.
Die elektrische Leitfähigkeit kannst du im Metall nun auch mit

berechnen. In dieser Formel steht  für die Anzahl der Elektronen,
für die Anzahl der Elektronen,  für die Elektronenladung,
für die Elektronenladung,  für die Masse des Elektrons und
für die Masse des Elektrons und  für die mittlere Flugzeit eines Elektrons zwischen zwei Stößen.
für die mittlere Flugzeit eines Elektrons zwischen zwei Stößen.
Elektrische Leitfähigkeit Tabelle
Die elektrischen Leitfähigkeiten sind für die meisten Materialien bereits gegeben. Du kannst einige davon in der nachfolgenden Tabelle herauslesen. Alle Werte aus dieser Tabelle gelten dabei für Raumtemperatur, also 25°C.
| Gruppe | Material | Elektrische Leitfähigkeit in sigma in S/m |
| Leiter | Silber | 62 · 106 |
| Kupfer | 58 · 106 | |
| Gold | 45,2 · 106 | |
| Aluminium | 37,7 · 106 | |
| Wolfram | 19 · 106 | |
| Messing | 15,5 · 106 | |
| Eisen | 9,93 · 106 | |
| Edelstahl (WNr. 1,4301) | 1,36 · 106 | |
| Halbleiter | Germanium (Dotierung -9) | 2 |
| Silizium (Dotierung -12) | 0,5 · 10-3 | |
| Elektrolytlösung | Meerwasser | ca. 5 |
| Leitungswasser | ca. 0,05 | |
| Destilliertes Wasser | 5 · 10-6 | |
| Isolator | Typischerweise | -8 |
Der spezifische Leitwert ist stark abhängig von der Temperatur, deshalb gelten die Werte auch nur bei 25°C. Mit steigender Temperatur wird die Gitterschwingung im Material höher. Das stört die Elektronen beim fließen und somit sinkt die elektrische Leitfähigkeit mit steigender Temperatur.
Die Tabelle haben wir in die Gruppen Leiter, Halbleiter, Elektrolytlösung und Isolator unterteilt. Du erkennst, dass Kupfer die zweithöchste elektrische Leitfähigkeit besitzt, weshalb in der Elektrotechnik sehr oft Kupferkabel genutzt werden. Silber hat sogar eine noch höhere Konduktivität, ist aber wesentlich teurer als Kupfer.
Interessant ist auch der Vergleich zwischen Meerwasser und destiliertem Wasser. Hier kommt die elektrische Leitfähigkeit aufgrund der gelösten Ionen im Wasser zustande. Meerwasser hat einen sehr hohen Anteil an Salz, welches sich im Wasser auflöst. Diese Ionen übertragen den Strom. Im destiliertem Wasser sind keine gelösten Ionen vorhanden, demnach kann so gut wie kein Strom fließen. Deswegen ist die elektrische Leitfähigkeit von Meerwasser sehr viel größer als die, von destiliertem Wasser.
Elektrische Leitfähigkeit Aufgaben
Zur Vertiefung betrachten wir zwei Beispielrechnungen.
Stell dir in der ersten Aufgabe vor, du hast einen 2m langen Draht mit einem Querschnitt von  . Der Widerstand des Drahtes beträgt bei Raumtemperatur
. Der Widerstand des Drahtes beträgt bei Raumtemperatur 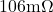 . Aus welchem Material besteht der Draht?
. Aus welchem Material besteht der Draht?
Die Lösung findest du, indem du die Formel  nach
nach  umformst. Dann erhältst du
umformst. Dann erhältst du
 .
.
Nun kannst du die gegebenen Werte einsetzten, dabei musst du darauf achten, dass du den Querschnitt in  umrechnest.
umrechnest.

Zum Schluss schlägst du in der Tabelle nach, welches Material eine Konduktivität von  hat, und kommst auf das Ergebnis, dass der Draht aus Aluminium ist.
hat, und kommst auf das Ergebnis, dass der Draht aus Aluminium ist.
In Aufgabe 2 ist dir nur der spezifische Widerstand einer Probe mit  gegeben. Aus welchem Material ist die Probe?
gegeben. Aus welchem Material ist die Probe?
Du kannst mit  die elektrische Leitfähigkeit ausrechnen. Nach einsetzen erhälst du
die elektrische Leitfähigkeit ausrechnen. Nach einsetzen erhälst du
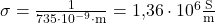 .
.
Schlägst du wieder in der Tabelle nach erfährst du, dass die Probe aus Edelstahl sein muss.
