Unbelasteter und belasteter Spannungsteiler
Du kannst nichts mit den Begriffen belasteter und unbelasteter Spannungsteiler anfangen? Dann bist du bei uns genau richtig. Wir erklären dir, wie du alle wichtigen Größen des Spannungsteilers berechnen kannst.
Inhaltsübersicht
Spannungsteiler einfach erklärt
Die Spannungsteilerformel kann dir dabei helfen Teilspannungen in einer Schaltung von passiven Bauelementen, zum Beispiel Widerständen zu bestimmen. Umgekehrt kann sie auch genutzt werden um eine bestimmte Spannung an einem Verbrauchen einzustellen. Häufig wird zwischen einem unbelasteten Spannungsteiler und einem belasteten Spannungsteiler unterschieden. Im Folgenden erklären wir dir was das genau bedeutet.
Unbelasteter Spannungsteiler
Als erstes schauen wir uns den unbelasteten Spannungsteiler an. Im einfachsten Fall besteht dieser aus einer Reihenschaltung von zwei Widerständen. Dementsprechend ist hier keine zusätzliche Last, also kein Verbraucherwiderstand, an den Ausgang der Schaltung, also parallel zu  angeschlossen.
angeschlossen.
Am Widerstand  kann also direkt die Ausgansspannung
kann also direkt die Ausgansspannung  entnommen werden.
entnommen werden.
Da der Strom in einer Reihenschaltung an jeder Stelle der selbe ist, gilt folgender Zusammenhang:

Durch Anwendung des Ohmschen Gesetzes folgt:

Diese Gleichung kann an dieser Stelle nach  umgestellt werden:
umgestellt werden:

Der Gesamtwiderstand des unbelasteten Spannungsteiler  kann nun durch Änderung der Widerstände R1 und R2 die Ausgangsspannung U2 variieren.
kann nun durch Änderung der Widerstände R1 und R2 die Ausgangsspannung U2 variieren.
Analog berechnet sich die Spannung  an
an  zu:
zu:

Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Spannungsteiler Formel
Allgemein gilt für die Spannung  am Widerstand
am Widerstand  in einer Reihenschaltung.
in einer Reihenschaltung.

Dabei gilt diese Formel unabhängig von der Anzahl der Widerstände in der Reihenschaltung, solange der Gesamtwiderstand  korrekt ermittelt wird.
korrekt ermittelt wird.
Unbelasteter Spannungsteiler Beispiel
In diesem Beispiel wird eine Reihenschaltung aus den zwei Widerständen  und
und  und der Spannungsquelle
und der Spannungsquelle  betrachtet. Gesucht sind die beiden Spannungen
betrachtet. Gesucht sind die beiden Spannungen  und
und  an den Widerständen.
an den Widerständen.
An dieser Stelle kann der Gesamtwiderstand der Schaltung ermittelt werden und die gegebenen Werte in die allgemeine Formel des Spannungsteilers eingesetzt werden:



Aus diesen Berechnungen geht hervor, dass die Teilspannungen zusammen die Gesamtspannung ergeben.

Durch Variation der Widerstände  und
und  können somit für
können somit für  und
und  beliebige Werte zwischen
beliebige Werte zwischen  und
und  eingestellt werden. Sind beispielsweise beide Widerstände identisch, teilt sich auch die Gesamtspannung zu gleichen Teilen auf die Widerstände auf.
eingestellt werden. Sind beispielsweise beide Widerstände identisch, teilt sich auch die Gesamtspannung zu gleichen Teilen auf die Widerstände auf.
Belasteter Spannungsteiler
Wird an den Ausgang des unbelasteten Spannungsteilers ein Lastwiderstand parallel geschalten, so sprechen wir von einem belasteten Spannungsteiler.
Es ergibt sich damit eine Schaltung in der sich  in Reihe zu der Parallelschaltung aus
in Reihe zu der Parallelschaltung aus 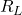 und
und  befindet.
befindet.
In diesem Fall ist es sinnvoll den Ersatzwiderstand  der Parallelschaltungen zu berechnen:
der Parallelschaltungen zu berechnen:

Dadurch vereinfacht sich die obige Schaltung zu einer Reihenschaltung aus  und
und  . Daher kann nun die gesuchte Spannung
. Daher kann nun die gesuchte Spannung  mit der allgemeinen Formel für den Spannungsteiler berechnet werden
mit der allgemeinen Formel für den Spannungsteiler berechnet werden

In einer Schaltung mit belastetem Spannungsteiler kann man nun beliebige Spannungen erzeugen und verwenden. Einziges Manko: Die Ausgangsspannung hängt vom Lastwiderstand ab, sodass die Schaltung bei Lastwechsel immer neu angepasst werden muss. Außerdem lassen sich Spannungen nur verkleinern, nicht aber vergrößern.


