Spezifischer Widerstand
Spezifischer Widerstand ist ein Begriff, über den du gerne mehr erfahren möchtest? Dann bist du an dieser Stelle genau richtig. Hier erfährst du unter anderem, was der spezifische Widerstand ist.
Wenn du eher der Video- statt Lesetyp bist, dann kannst du dir gerne unser Video zum spezifischen Widerstand ansehen.
Inhaltsübersicht
Spezifischer Widerstand einfach erklärt
Der spezifische elektrische Widerstand (kurz spezifischer Widerstand oder auch Resistivität) ist eine Proportionalitätskonstante, die das Berechnen von elektrischen Widerständen abhängig von ihren geometrischen Abmessungen ermöglichen soll. Welchen Wert diese Konstante besitzt, hängt unter anderem vom Material des elektrischen Widerstands und seiner Temperatur ab. In diesem Sinne ist der spezifische Widerstand eine temperaturabhängige Materialkonstante.
Die Beziehung zwischen dem elektrischen Widerstand eines Leiters auf der einen und seinen geometrischen Abmessungen auf der anderen Seite wird durch den spezifischen Widerstand vermittelt.
Der Zusammenhang zwischen elektrischer Widerstand und geometrischen Abmessungen ist
.
Hier ist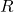 
der elektrische Widerstand in Ohm (
), 
die Länge des Leiters in Meter (
), 
die über die gesamte Länge gleichbleibende Querschnittsfläche in 
und 
der spezifische Widerstand in 
. Der Kehrwert des spezifischen Widerstands heißt elektrische Leitfähigkeit.
Wie du den Widerstand messen kannst, zeigen wir dir in diesem Video !
Experimentelle Ableitung
Stell dir vor, du hättest zwei Widerstände vor dir liegen, die zwar die exakt gleiche Länge besitzen, aber ihre Querschnittsflächen sind unterschiedlich. Bezeichnen wir den Widerstand des Leiters mit der kleineren Querschnittsfläche als 
(k für klein) und den des anderen Leiters als 
(g für groß).
In diesem Beitrag veranschaulichen wir den Widerstand als eine Tür, durch die eine Menschenmenge (symbolisch für den Strom) hindurchgehen möchte. Übernehmen wir diese Analogie, dann können wir festhalten, dass
gilt.
Durch eine größere Tür (Leiter mit größerer Querschnittsfläche) passt die Menschenmenge leichter hindurch als durch eine kleinere Tür (Leiter mit kleinerer Querschnittsfläche). Nach dem Ohmschen Gesetz gilt
und da durch den Leiter mit größerer Querschnittsfläche mehr Strom fließt, ist sein Widerstand kleiner.
Betrachten wir nun die Situation, in der die beiden Widerstände die exakt gleiche Querschnittsfläche, aber unterschiedliche Längen besitzen. Wir bezeichnen wie davor die Widerstände mit für den Leiter mit der größeren Länge und für den anderen Leiter.
In unserer Analogie mit der Menschenmenge ist die Wahrscheinlichkeit, dass zwei Menschen aneinander stoßen, größer, je länger der Weg von der Eingangs- zur Ausgangstür ist. Eine Person könnte daher so oft mit anderen Personen aneinander stoßen, dass sie die Orientierung verliert und es nicht zur Ausgangstür schafft. Das heißt, der Stromfluss durch den längeren Leiter ist geringer als der durch den kürzeren Leiter. Wieder nach dem Ohmschen Gesetz gilt dann
.
Diese beiden Beobachtungen können wir durch folgende Proportionalitäten ausdrücken
und
.
Um diese Proportionalitäten in Form einer einzigen Gleichung wiederzugeben, führen wir die Proportionalitätskonstante ein und erhalten
.
Das ist gerade die Formel aus dem vorherigen Abschnitt, wo der spezifische Widerstand ist.
Temperaturabhängigkeit
Der spezifische Widerstand besitzt eine bestimmte Temperaturabhängigkeit. Im Allgemeinen steigt der Widerstand von Leitern, wenn die Temperatur ansteigt. Das liegt daran, dass die Atome im Leiter kräftiger schwingen und dadurch die Bewegung der Elektronen durch den Leiter stärker behindern können. Ist die Temperaturänderung nicht zu groß, dann besteht zwischen elektrischen Widerstand und Temperaturänderung der folgende lineare Zusammenhang
.
Hier ist 
der spezifische Widerstand bei einer bestimmten Referenztemperatur (etwa 20 °C), 
der spezifische Widerstand bei einer Temperatur 
und 
der Temperaturkoeffizient.
Je nach Vorzeichen des Temperaturkoeffizienten unterschiedet man zwischen Heißleitern (
) und Kaltleitern (
). Der spezifische Widerstand und somit auch der elektrische Widerstand steigt demnach bei Kaltleitern mit steigender Temperatur, und sinkt bei Heißleitern mit steigender Temperatur.
Spezifischer Widerstand ausgewählter Materialien
In diesem Abschnitt stellen wir dir eine Tabelle mit den spezifischen Widerständen von ausgewählten Materialien vor.
| Material | Spezifischer Widerstand in |
| Aluminium |  |
| Eisen |
 bis 
|
| Germanium |  |
| Glas |
 bis 
|
| Konstantan |  |
| Kupfer |  |
Da der spezifische Widerstand temperaturabhängig ist, muss bei solchen Tabellen immer die Temperatur angegeben werden, für die die Werte gemessen wurden. So ist beispielsweise bei 20°C der spezifische Widerstand von Kupfer 
und der spezifische Widerstand von Aluminium 
. Beides sind kleine Zahlen, weswegen ihre elektrische Leitfähigkeit groß ist. Das war auch zu erwarten, denn Aluminium und Kupfer gelten als gute Leiter. Ein Isolator wie Glas hingegen hat einen sehr hohen spezifischen Widerstand. Die Werte des spezifischen Widerstands für Halbleiter befinden sich irgendwo dazwischen, auch wenn keine klaren Grenzen existieren.
Spezifischer Widerstand berechnen
Schauen wir uns zum Abschluss ein kleines Beispiel an. Angenommen wir haben einen runden Leiter aus Kupfer der Länge 
mit einem Radius von 
. Welchen elektrischen Widerstand wird dieser Leiter besitzen?
Da es sich um einen runden Leiter handelt, können wir dir Querschnittsfläche folgendermaßen berechnen
.
Der elektrische Widerstand ergibt sich dann zu
.
Wir haben hier den spezifischen Widerstand für Kupfer der Tabelle von oben entnommen.