Stern-Dreieck-Umwandlung Übung
In diesem Beitrag schauen wir uns die Stern-Dreieck-Umwandlungen an einfachen Beispielen an.
Inhaltsübersicht
Stern-Dreieck-Umwandlung Beispiel
In unserem Beispiel wollen wir den Ersatzwiderstand einer Brückenschaltung berechnen, die mit folgenden Widerständen besetzt ist und so aussieht:
Da wir hier keine Reihen- bzw. Parallelschaltung haben, ist es für uns unmöglich den Ersatzwiderstand mit einfachen Mitteln zu berechnen. Wir müssen unsere Schaltung also so verändern, dass wir am Schluss nur noch parallel und in Reihe geschaltete Widerstände haben. Und hier kommt jetzt unsere Stern- und Dreieckschaltung ins Spiel bzw. deren Transformationen. Um die Umwandlung in beide Richtungen, also von Stern in Dreieck und von Dreieck in Stern zu zeigen, werden wir das Beispiel auf beide Arten rechnen.
Umwandlung Sternschaltung in Dreieckschaltung
[[ jump_to_video 00:57]]
Fangen wir zunächst mit der Stern-zu-Dreieck-Transformation an. Durch diese Transformation bekommen wir eine reine Parallel- und Reihenschaltung der Widerstände, mit der wir ganz einfach den Ersatzwiderstand berechnen können. Als erstes suchen wir uns die Sternschaltung mit R1, R3 und R5 aus und beschriften deren Klemmen mit 1, 2 und 3. Im zweiten Schritt tauschen wir die Sternschaltung durch eine Dreieckschaltung aus. Dazu entfernen wir einfach die Widerstände R1, R3 und R5 aus der Schaltung.
Zurück bleiben der R2 und der R4 und unsere drei eingezeichneten Klemmpunkte. Zwischen diesen zeichnen wir nun drei neue Widerstände als Dreieckschaltung und benennen sie anhand der Klemmen, zwischen denen sie angeschlossen sind. Die Widerstände müssen jetzt auf jeden Fall anders heißen, da sie auch andere Werte haben! Beschrifte sie am besten nach dem simplen Zahlenschema, bei dem die Indizes den Klemmennummern entsprechen. Für den Fall, dass du die entstandene Reihen- und Parallelschaltung nicht auf Anhieb siehst, haben wir die Schaltung noch einmal umgezeichnet.
Nun geht es an die Berechnung der Werte für  ,
,  und
und  . Solltest du Dir schwer tun die Widerstände R1, R3 und R5 in die Formeln einzutragen, notiere dir die Beschreibungen mit den Klemmen daneben, also
. Solltest du Dir schwer tun die Widerstände R1, R3 und R5 in die Formeln einzutragen, notiere dir die Beschreibungen mit den Klemmen daneben, also 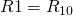 ,
,  und
und  . In unserer Berechnung wollen wir die echten Bezeichnungen der Widerstände benutzen. Als Erstes rechnen wir den Zähler Z aus, der bei einer Stern-zu-Dreieck-Umwandlung immer der gleiche ist:
. In unserer Berechnung wollen wir die echten Bezeichnungen der Widerstände benutzen. Als Erstes rechnen wir den Zähler Z aus, der bei einer Stern-zu-Dreieck-Umwandlung immer der gleiche ist:
Damit können wir nun die Dreieckswiderstände ganz einfach ausrechnen. Diese Werte setzen wir nun in unser Bild mit der reinen Reihen- und Parallelschaltung ein und können so bequem den Ersatzwiderstand von 6,24 Ω ausrechnen.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Umwandlung Dreieckschaltung in Sternschaltung
Jetzt wollen wir die gleiche Schaltung rechnen, aber diesmal wandeln wir eine Dreieckschaltung in eine Sternschaltung um, damit du siehst, dass am Schluss der gleiche Wert für den Ersatzwiderstand herauskommt.
Auch hier suchen wir uns zunächst die Dreieckschaltung mit R1, R2 und R3 aus und beschriften die drei Klemmpunkte mit 1, 2 und 3. Dann entfernen wir die Widerstände der Dreieckschaltung. Übrig bleiben der R4 und der R5, sowie unsere drei Klemmpunkte. Zwischen den Klemmen zeichnen wir nun eine Sternschaltung und bezeichnen die Widerstände anhand der Klemmen, über die sie mit dem Sternpunkt verbunden sind. Durch diese Umformung entsteht nun eine Schaltung, die nur aus Reihen- und Parallelschaltung besteht und von der du ganz einfach den Ersatzwiderstand ausrechnen kannst. Für den Fall, dass du noch nicht ganz erkennst, wie einfach unsere Schaltung jetzt geworden ist, haben wir sie für dich umgezeichnet.
Nun wollen wir die Werte für 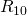 ,
,  und
und  berechnen. Wie bei der vorherigen Aufgabe, gilt auch hier: Tust du dir schwer beim Einsetzen der realen Widerstandsbezeichnungen in die Formeln, schreibe dir als Hilfe die Standardnamen der Dreieckschaltung daneben:
berechnen. Wie bei der vorherigen Aufgabe, gilt auch hier: Tust du dir schwer beim Einsetzen der realen Widerstandsbezeichnungen in die Formeln, schreibe dir als Hilfe die Standardnamen der Dreieckschaltung daneben:  ,
,  und
und  . Wir verwenden wieder die realen Bezeichnungen.
. Wir verwenden wieder die realen Bezeichnungen.
Als Erstes berechnen wir die Summe der Dreieckswiderstände für unseren Nenner N. Nun können wir die Sternwiderstände ausrechnen: Diese Werte setzen wir nun in unser Ersatzschaltbild und können so durch zusammenfassen der Widerstände den Ersatzwiderstand von 6,24 Ω ausrechnen. Es kommt das gleiche heraus wie bei der Stern-zu-Dreieck-Transformation und das muss auch so sein, denn es ist ja die gleiche Schaltung.
Jetzt weißt du, wie du Stern- und Dreieckschaltungen ineinander umwandelst und hast hoffentlich erkannt, wie hilfreich das sein kann.




