Elektrisches Potential

Elektrisches Potential einfach erklärt 

In der klassischen Mechanik kann die Betrachtung eines Problems aus der Perspektive der Energie die Situation, im Vergleich zur Betrachtung aus der Perspektive der Kräfte am System, erheblich vereinfachen. Insbesondere die Tatsache, dass die Energie eine Erhaltungsgröße ist, spielt in diesem Zusammenhang eine wesentliche Rolle.

Auch in der klassischen Elektrodynamik erweist sich die Betrachtung auf Energieebene für sehr nützlich. Es wird daher das elektrische Potential (auch als elektrostatisches Potential) als der Quotient aus potentieller Energie  einer Probeladung und ihrer Ladungsmenge

definiert.

Die Möglichkeit ein solches elektrisches Potential überhaupt definieren zu können, liegt darin begründet, dass das elektrische Feld einer Ladungsverteilung und die daraus resultierende elektrostatische Kraft auf eine Probeladung eine konservative Kraft ähnlich zur Gravitationskraft ist.

Elektrisches Potential hat die Einheit Volt () oder auch Joule pro Coulomb ().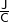

Elektrisches Potential Formel

In diesem Abschnitt stellen wir dir zwei wichtige Formeln für das elektrische Potential bestimmter Ladungsverteilungen vor. Wir besprechen auch kurz die Analogie zwischen elektrisches Potential und Gravitation.

Plattenkondensator

Wir betrachten die Situation, bei der sich zwei ebene Platten parallel in einem Abstand zueinander befinden. Zusätzlich sei eine der beiden Platten positiv, die andere negativ geladen. Eine solche Zusammenstellung heißt auch Plattenkondensator . Bezeichnen wir einen Punkt auf der positiven Platte mit und einen Punkt auf der negativen Platte mit . Es ergibt sich dann für die Potentialdifferenz zwischen diesen zwei Punkten

.

Hier ist der Betrag des als homogen angenommenen elektrischen Feldes zwischen den beiden Platten. Eine solche Potentialdifferenz wird auch als elektrische Spannung bezeichnet, die zwischen diesen beiden Punkten herrscht.

Wir können aus dieser Gleichung erkennen, dass elektrisches Potential an der positiv geladenen Platte (Platte A) höher als das Potential an der negativ geladenen Platte (Platte B) ist. Eine positive Ladung innerhalb des Plattenkondensators bewegt sich deshalb in Richtung der negativen Platte. Allgemein gilt, dass das elektrische Feld – und somit die Bewegungsrichtung einer positiven Ladung – in die Richtung zeigt, in der das elektrische Potential am schnellsten abnimmt.

direkt ins Video springen

Analogie zum Gravitationsfeld

Wenn wir die obere Gleichung mit der Ladungsmenge einer Probeladung multiplizieren und annehmen, dass die negativ geladene Platte ein elektrisches Potential von Null besitzt, dann gilt für die elektrische potentielle Energie im Abstand von der Platte B 

.

Hier bezeichnet das elektrische Potential an der Stelle der Probeladung.

Vergleichen wir diese Gleichung mit der potentielle Energie in einem homogenen Gravitationsfeld

.

Wir erkennen, dass die Ladungsmenge die Rolle der Masse und der Betrag des elektrischen Feldes die Rolle der Schwerebeschleunigung spielen. Eine Masse, die sich in der Höhe über den Boden befindet, beschleunigt durch die Gravitation der Erde in Richtung Boden. Die Masse bewegt sich also in die Richtung, in die seine potentielle Energie abnimmt. Auf ähnliche Weise bewegt sich eine positive Ladung in die Richtung, in die seine elektrische potentielle Energie abnehmen würde. Da elektrische potentielle Energie und elektrisches Potential linear zusammenhängen, ist diese Beobachtung analog dazu, dass sich das positiv geladene Teilchen in Richtung abnehmenden elektrischen Potentials bewegt.

direkt ins Video springen

Ähnlich zur potentiellen Energie macht nur die Potentialdifferenz physikalisch Sinn, denn bei der Definition des elektrischen Potentials muss man einen Bezugspunkt willkürlich festlegen, von dem aus dann andere Orte im Raum bezeichnet werden können. In diesem Sinne hat elektrisches Potential für sich keine echte physikalische Bedeutung, da für ein gegebenen Punkt im Raum sein Wert durch die Wahl eines anderen Bezugspunktes verändert werden kann. Elektrisches Potential verhält sich also in gewisser Weise wie die Höhe, weil über die Höhe sich erst nach Festlegung eines Bezugspunktes reden lässt. 

Auf einer topographischen Karte werden Wege, bei denen sich die Höhe nicht ändert, als Höhenlinien bezeichnet. Analog heißen Wege, entlang denen das elektrische Potential konstant ist, Äquipotentiallinien.

direkt ins Video springen

Geladenes Teilchen

Nehmen wir an, dass sich ein Teilchen der Ladungsmenge im Ursprung eines von uns gewählten Koordinatensystems befindet. Die Position eines weiteren Punktes sei und sei der Abstand der zwei Punkte. Für das elektrische Potential an der Stelle gilt dann

.

Hier bezeichnet die elektrische Feldkonstante.

Bei dieser Gleichung geht man davon aus, dass man eine positive Probeladung aus dem Unendlichen unter Einfluss des elektrischen Feldes an die Position bringt.

Elektrisches Potential berechnen

Lass uns zum Abschluss ein kleines Beispiel gemeinsam rechnen.  Nehmen wir hierzu an, dass ein Elektron von der negativ geladenen Platte zur positiv geladenen Platte über eine Potentialdifferenz von beschleunigt wird. Wie ändert sich die potentielle Energie des Elektrons?

Für die Differenz im elektrischen Potential zwischen den beiden Platten gilt

,

umgestellt auf die gesuchte Änderung der potentiellen Energie erhalten wir

.

Die Ladungsmenge eines Elektrons beträgt und daher bekommen wir

.

Beachte, dass für die Einheit Volt gilt. Zusätzlich haben wir hier angenommen, dass die Platte mit dem Punkt B positiv geladen ist, weswegen kein Minuszeichen vor steht. Die Rechnung zeigt, dass die potentielle Energie des Elektrons abnimmt.